Axisymmetric Slow Motion of a Prolate Particle in a Circular Capillary with Slip Surfaces
2017-03-19HongYehHuanKeh
Hong Y. Yeh, Huan J. Keh*
1 Introduction
The creeping motions of small particles in viscous fluids are of much fundamental and practical interest in many areas of science and technology. The theoretical treatment of this subject grew out of the classic work of Stokes (1851) for a no-slip spherical particlemigrating in an unbounded, incompressible, Newtonian fluid. Oberbeck (1876) extended this analysis to the migration of an ellipsoid. More recently, analytical results of low-Reynolds-number motions were obtained for a particle whose boundary conforms to a coordinate surface of one orthogonal curvilinear coordinate system in which the Stokes equations are simply separable [Payne and Pell (1960)] or semi-separable [Dassios,Hadjinicolaou, and Payatakes (1994)], for a slightly deformed sphere [Brenner (1964)],and for a slender body [Batchelor (1970)]. Additionally, the creeping motions of a particle of specific or general shape have been investigated semi-analytically by using the boundary collocation method [Gluckman, Pfeffer, and Weinbaum (1971)], boundary integral method [Youngren and Acrivos (1975)], and singularity method [Chwang and Wu (1975)].
When one tries to solve the creeping-flow problems, no-slip boundary conditions are usually taken at the solid-fluid interfaces. Although this assumption is validated by experimental evidences at macroscopic scales, it is seldom accepted microscopically [Pit,Hervet and Leger (2000); Martini et al. (2008)]. The phenomena that the adjacent fluid slips frictionally over a solid surface occur in many cases, such as the rarefied gas flow past an aerosol particle [Ying and Peters (1991); Keh and Shiau (2000)], liquid flow next to a lyophobic surface [Churaev, Sobolev, and Somov (1984); Gogte et al. (2005)],micropolar fluid flow around a rigid particle [Sherif, Faltas, and Saad (2008)], and viscous fluid flow over the surface of a porous medium [Saffman (1971); Nir (1976)] or a small particle of molecular size [Hu and Zwanzig (1974)]. Presumably, any such slipping would be proportional to the local shear stress of the fluid adjacent to the solid surface[Felderhof (1977); Keh and Chen (1996)], known as Navier’s slip [Eqs. (4) and (5)], and the proportionality constantβ-1is termed the slip coefficient of the solid-fluid interface.The drag force acting on a migrating spherical particle of radiusb with a slip surface by an unbounded fluid of viscosityηcan be expressed as [Basset (1961); Happel and Brenner (1983)]

The analysis of creeping motion of a no-slip particle which deforms slightly in shape from a sphere in an arbitrary direction pioneered by Brenner (1964) was extended to a slightly deformed slip sphere and closed-form expressions for the hydrodynamic drag force exerted on it were obtained to the first order [Palaniappan (1994); Senchenko and Keh (2006)] and second order [Chang and Keh (2009)] in the small parameter characterizing the deformation. On the other hand, the semi-separable general solution in the form of an infinite series expansion for the axisymmetric creeping flow in spheroidal coordinates developed by Dassios, Hadjinicolaou, and Payatakes (1994) was used to examine the slip flow past a spheroid and to derive the drag force experienced by it in explicit forms [Deo and Datta (2002); Keh and Chang (2008)]. Recently, the creeping flows caused by a general axisymmetric particle with a slip surface migrating parallel[Keh and Huang (2004); Wan and Keh (2009)] and perpendicular [Chang and Keh (2011)]to its axis of revolution have been studied semi-analytically by using a method of internal singularity distribution incorporated with a boundary collocation technique.
In real situations of colloidal motion, particles are seldom isolated and will move in the presence of confining boundaries. Therefore, the boundary effects on creeping motion of particles with fluid slip at the solid surfaces are essential and have been investigated for various cases of a confined sphere [Reed and Morrison (1974); Chen and Keh (1995);Keh and Chang (1998); Lu and Lee (2002); Chen and Keh (2003); Chang and Keh (2006);Keh and Chang (2007); Keh and Lee (2010); Faltas and Saad (2011); Lee and Keh (2013,2014); Chiu and Keh (2016, 2017); Li and Keh (2017)]. Recently, the axisymmetric translation [Keh and Chang (2010)] and rotation [Wan and Keh (2011)] of a slip particle of revolution at an arbitrary position between two parallel plane walls have also been studied using the method of distributed internal singularities. In the current article, we adopt the same method to analyze the creeping flow caused by a general prolate particle of revolution undergoing axially symmetric migration in a circular capillary with slip surfaces.The drag forces acting on a spheroid and a Cassini oval (which has various configurations from a sphere to a partially concave body as its shape parameter takes different values) by the suspending fluid are numerically calculated with good convergence for broad ranges of the particle shape parameter, particle-to-capillary size ratio, and normalized slip coefficients.These results agree excellently with those available in the literature for the particular cases of a slip sphere, a no-slip spheroid, and a no-slip Cassini oval migrating in the capillary.
2 Mathematical formulation of the general problem
Consider the steady creeping motion of an axially symmetric, prolate particle along its axis of revolution which is also the centerline of a circular capillary of radiusR filled with a quiescent, incompressible, Newtonian fluid of viscosityη, as shown in Fig.1.Here(ρ,φ,z)and(r,θ,φ)are the circular cylindrical and spherical coordinate systems,respectively, with the origin at the center of the particle. The particle migrates with a velocity, whereis the unit vector in thedirection. The fluid may slip frictionally at the particle surface Spand at the capillary wallρ=R.

Figure 1: Geometrical sketch for the migration of an axisymmetric prolate particle along its axis of revolution in a coaxial circular capillary.
The Reynolds number is sufficiently small so that the fluid motion is governed by the Stokes equations,


is the viscous stress tensor,is the unit vector in thedirection,is the unit normal vector on the particle surfacepointing into the fluid,is the unit dyadic, and the constantsare the Navier slip coefficients about the particle surface and capillary wall, respectively.
To solve Eqs. (2) - (6) for the axially symmetric motion, a set of spherical singularities satisfying Eqs. (2), (3), (5), and (6) will be distributed along the axis of revolution inside the particle. The fluid flow field is constructed by the superposition of these singularities and the boundary condition (4) over the particle surface can be satisfied by using a multipole collocation method.
The fluid velocity components in circular cylindrical coordinates caused by a spherical singularity at the pointρ =0and z =hare [Keh and Chang (2007)]a



A segment along the axis of revolution (ρ =0) between the points z =c1≤0and z=c2≥0within the particle is taken on which a set of spherical singularities are distributed. The general solution of the fluid velocity can be approximated by the superposition of these singularities into the integral form of Eqs. (7) and (8),

where Bn(t)and Dn(t)are the unknown density distribution functions.
In order to use the boundary collocation method, we apply the M-point Gauss-Legendre quadrature of integration [Hornbeck (1975)] to Eq. (10) and truncate the infinite seriesafter terms to result in


Substituting Eqs. (11) and (12) into Eq. (4), we obtain



In the next two sections, the above-described semi-analytical procedure will be taken to solve for the axisymmetric motions of a prolate spheroid and a prolate Cassini oval,respectively, in a circular capillary. In both cases, the streamline geometry is symmetric about z and only the terms with even nare retained in Eqs. (11) - (13). For the simple case of migration of a spherical particle (can be degenerated from either spheroid or Cassini oval) along the axis of the circular capillary with slip surfaces, only one singularity at the particle center (with h =0) is needed and the numerical results of the drag force have been obtained by Keh and Chang (2007).
3 Motion of a prolate spheroid
In this section, we consider the migration of a prolate spheroid along its axis of revolution in a coaxial circular capillary, where the fluid is allowed to slip at the solid surfaces.The surface of a prolate spheroid and the local components of its unit normal in Eqs. (14)and (15) are given by


The method of combined singularity distribution and boundary collocation presented in the previous section is used to obtain the solution for the axisymmetric migration of a prolate spheroid in a circular capillary with slip surfaces. The details of the numerical scheme used for this work were given in an earlier paper [Keh and Chang (2010)], in which excellent accuracyand convergence behavior were achieved. Our solutions of thehydrodynamic dragforceexerted on the confined prolate spheroid normalized by the corresponding drag acting on an unconfined spheroid (i.e., as) are presented in Tables1 and 2 for various values of the particle aspect ratio, particle slip parameter, wall slip parameter and particle-wall spacing parameter. The results converge to at least the significant figures as given. For the difficult case ofthe number of collocation points withsufficiently large to achieve this convergence. For the special cases of andisour results are in excellent agreement with the available solutions for the axisymmetric motions of a slip sphere in a slip circular capillary [Keh and Chang(2007)] and of a no-slip spheroid in a no-slip capillary [Yeh and Keh (2013)],respectively.
The numerical results for the normalized hydrodynamic drag force F /F0(or viscous retardation) for the axially symmetric migration of a prolate spheroid with aspect ratioin a circular capillary as functions of the spacing parameter b /Rand particle slip parameterβb/ηare plotted in Fig. 2 for the limiting cases of no-slip capillary walland perfect-slip capillary wall. Analogous to the corresponding motion of a spherical particle, Tables 1 and 2 as well as Fig. 2 show that the approach of the capillary wall can significantly enhance the hydrodynamic drag experienced by the spheroid. For a spheroid with given values ofandincreases monotonically with an increase in the ratiofrom unity atto infinity in the touching limitThe normalized wall-corrected drag force exerted on the spheroid in general decreases with decreases in(i.e., with increasing slippage at the solid surfaces), keepingandunchanged. Interestingly, when the capillary wall does not slip much (with a large value ofand the value ofis close to unity (especially asis large),first decreases with an increase inreaches a minimum at some finite value oand then increases with increasingto the limit

Figure 2a: Plots of the normalized drag force F /F0for the axially symmetric migration of a prolate spheroid with a /b =2in a circular capillary for various values of the spacing parameter b/Rand particle slip parameterβb /η: (a) F /F0versus b/R; (b)F/F0versusβb /η. The solid and dashed curves represent the cases ofbη→ ∞and β wb /η=0, respectively.

Figure 2b: Plots of the normalized drag force F /F0for the axially symmetric migration of a prolate spheroid with a /b=2in a circular capillary for various values of the spacing parameter b /Rand particle slip parameterβb /η: (a)F/F0versus b/R; (b) F /F0versusβb/η. The solid and dashed curves represent the cases of /η→ ∞and /η=0, respectively.
In Fig. 3, the results of the normalized drag force F /F0for the axially symmetric migration of a prolate spheroid withβb /η→ ∞and βb/η=0in a circular capillary withare plotted versusfor various values of b /R. Tables 1 and 2 as well as Fig. 3 indicate that, for given values of b /R,βb /η, andβwb/η, the ratio F /F0in general is an increasing function of a /b, since the increase in the surface area of the spheroid for its viscous interaction with the capillary wall enhances the hydrodynamic resistance to the motion of the particle. However, whenβb/η→0and eitherdecreases with an increase in(and a minimum ofcan appear at some intermediate value ofis large), due to the slippage at the particle surface. In general,is not a very sensitive function of
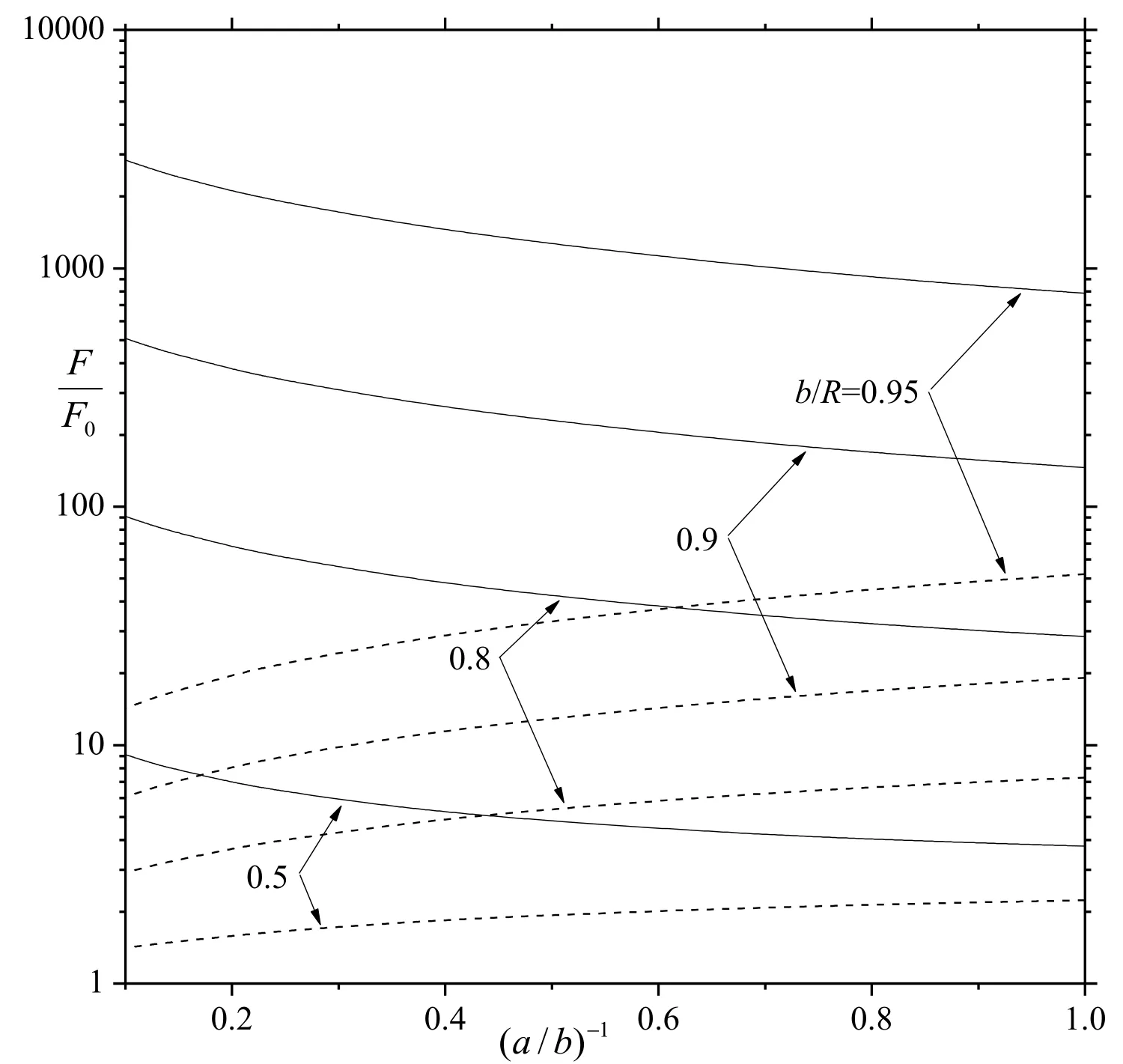
Figure 3: Plots of the normalized drag force F /F0for the axially symmetric migration of a prolate spheroid in a circular capillary with /η=0versus the reciprocal of particle aspect ratio ( a /b)-1for various values of the spacing parameterb /R. The solid and dashed curves represent the cases ofβb/η→ ∞andβb /η=0, respectively.

Table 1: The normalized drag force F /F0exerted on a prolate spheroid migrating axi-symmetrically in a circular capillary withβwb/η→∞at various values of the parameters a /b, b /R, and βb/η

0.9 469.170 501.699 749.832 1248.51 1679.50 0.95 2806.65 3013.32 4569.68 7644.97 10264.2 0.975 16290.8 1.756E4 2.668E4 4.431E4 5.85E4

Table 2: The normalized drag force F /F0exerted on a prolate spheroid migrating axisymmetrically in a circular capillary withβw =βat various values of the parameters a/b, b /R, and βb/η.
4 Motion of a prolate Cassini oval
The method of combined singularity distribution and boundary collocation is used in this section to solve for the hydrodynamic drag force experienced by a prolate Cassini oval undergoing axial symmetric migration in a circular capillary with slip surfaces. The surface of a prolate Cassini oval [Keh and Tseng (1994)] and the local components of its outward unit normal in cylindrical coordinates are expressed by

and

In Tables 3 and 4, numerical results of the drag forceexerted by the fluid on a prolate Cassini oval migrating axi-symmetrically in a circular capillary normalized by its valuein an unbounded fluidare presented for various values of the slip parametersparticle shape parameter(up to 0.95), and particle-wall spacing parameter(up to 0.975), whereis the larger one betweenAgain, our solutions for the limiting cases of(same as those given for the case ofin Tables 1 and 2) andagree excellently with the results for the axisymmetric motions of a slip sphere in a slip circular capillary [Keh and Chang (2007)] and of a no-slip Cassini oval in a no-slip capillary [Yeh and Keh (2013)], respectively.
Numerical values of the normalized hydrodynamic drag forcefor the axially symmetric migration of a prolate Cassini oval with shape parametein a circular capillary as a function of the spacing parameterand particle slip parameterare plotted in Fig. 4 for the cases of no-slip capillary walland perfect-slip capillary wallSimilar to the corresponding motion of a slip prolate spheroid considered in the previous section, Tables 3 and 4 as well as Fig.4 also show that the approach of the capillary wall can substantially increase the hydrodynamic drag experienced by the slip Cassini oval. For a Cassini oval with a given shape parameteincreases monotonically with an increase in the ratio b /Rfrom unity at b /R =0to infinity in the touching limit b/R =1, and in general decreases with decreases in βb /ηandβwb/η. Again, when the capillary wall does not slip much and the value of b /Ris close to unity, F /F0first decreases with an increase inβb/ηfromβb/η=0before attaining a minimum, and then increases with a further increase inβb/η.

0.2 1.70173 1.76840 1.89405 2.03118 2.09774 2.10648 0.4 3.70451 4.04497 4.71003 5.31421 5.29098 5.23439 0.6 11.6571 13.3944 17.1162 19.6686 17.8918 17.3608 0.8 79.9433 97.0826 141.978 155.944 125.345 120.368 0.9 507.226 637.551 1063.90 1037.97 790.890 759.547 0.95 3050.36 3919.74 7511.60 6214.28 4723.97 4522.7 0.975 17748.3 23094.7 50904.0 35308.8 27262 2.6E4

Table 4: The normalized drag force F /F0exerted on a prolate Cassini oval migrating axi-symmetrically in a circular capillary withβw =βat various values of the parameters(c /d)2, b /R, and βb/η.

0.95 344.508 383.401 566.270 464.278 334.720 317.3 0.975 1.05E3 1176 1954.78 1383.1 991 9.4E2

Figure 4a: Plots of the normalized drag force F/F0for the axially symmetric migration of a prolate Cassini oval with ( c /d)2=0.8in a circular capillary for various values of the spacing parameter b /Rand particle slip parameter βb /η: (a)F/F0; (b) F /F0versus βb/η. The solid and dashed curves represent the cases of βwb/η→ ∞and =0, respectively.

Figure 4b: Plots of the normalized drag force F /F0for the axially symmetric migration of a prolate Cassini oval with ( c /d)2=0.8in a circular capillary for various values of the spacing parameter b /Rand particle slip parameterβb /η: (a) F /F0versus b /R;(b) F /F0versusβb/η. The solid and dashed curves represent the cases of βw b /η→ ∞and /η=0, respectively.

Figure 5: Plots of the normalized drag force 0/FF for the axially symmetric migration of a prolate Cassini oval in a circular capillary with 0/βb w =ηversus the particle shape parameter 2). The solid and dashed curves represent the cases of∞→ηβ/b( dc/for various values of the spacing parameter Rb/and 0/=ηβb , respectively.
In Fig. 5, the results of the normalized drag force F /F0for the axially symmetric migration of a prolate Cassini oval with βb /η→ ∞and βb/η=0in a circular capillary with βwb/η=0as a function of its shape parameterfor various values of the spacing parameter b /Rare plotted. Tables 3 and 4 as well as Fig. 5 indicate that, for a given value of b /Rand a relatively large value of βb/ηor βwb /η, the ratio F /F0in general increases with an increase in ( c /d)2in the range of 0 ≤ ( c/d)2≤1/2(due to the increase in the surface area of the Cassini oval for its viscous interaction with the capillary wall), but can reach a maximum at a value of(c/d)2>1/2(this value increases with decreasing b /R) and then decrease with a further increase in ( c /d)2(because the increase in the concave portion of the Cassini oval reduces the hydrodynamic retardation effect of the capillary wall). However, when βb/η→0and eitherβwb /ηor b /Ris small, F /F0can first decrease with an increase in ( c /d)2, reach a minimum at some value of ( c /d)2, and then increase with a further increase in ( c /d)2, due to the slippage at the particle surface. For the case of large b /Rand small to moderate βb /ηand βwb /η, F /F0can encounter both a minimum and a maximum with an increase in ( c /d)2in the whole range. Also, F /F0is not a very sensitive function of ( c /d)2in the whole range, but the boundary effect on the migration of the particle is significant.
5 Conclusions
The creeping motion of an axisymmetric prolate particle along its axis of revolution in a coaxial circular capillary with slip-flow surfaces is examined by using the method of combined singularity distribution and boundary collocation. The convergent and accurate solutions of the normalized hydrodynamic drag force F /F0for the axially symmetric migrations of a prolate spheroid and of a prolate Cassini oval are obtained for broad ranges of the particle aspect ratio a /band shape parameter, respectively, the particle-wall separation parameterb /R, the particle slip parameter βb/η, and the wall slip parameterβwb /η. For constant values o, the normalized drag F /F0in general decreases with decreasing(increasing slippage at the solid surfaces), but there are exceptions when the values of bothare large. For given values of b/R,βb /η, andβwb/η, the normalized dragincreases with an increase in the axial-to-radial aspect ratio of the particle (or effective surfacearea for the particle-wall hydrodynamic interaction), but this trend can be reversed as is small (the particle is highly slippery). The boundary effect of the capillary wall on the migration of the particle is significant when they are close to each other.
Appendix A: Definitions of functions in Section 2. Some functions in Section 2 are defined a s



Basset, A. B. (1961): A treatise on hydrodynamics, vol. 2, Dover, New York.
Batchelor, G. K. (1970): Slender-body theory for particles of arbitrary cross-section in Stokes flow. J. Fluid Mech., vol. 44, pp. 419-440.
Brenner, H. (1964): The Stokes resistance of a slightly deformed sphere. Chem. Eng. Sci.,19, 519-539.
Chang, Y. C.; Keh, H. J. (2006): Slow motion of a slip spherical particle perpendicular to two plane walls. J. Fluids Structures, vol.22, pp.647-661.
Chang, Y. C.; Keh, H. J. (2009): Translation and rotation of slightly deformed colloidal spheres experiencing slip. J. Colloid Interface Sci., vol.330, no.1, 201-210.
Chang, Y. C.; Keh, H. J. (2011): Theoretical study of the creeping motion of axially and fore-and-aft symmetric slip particles in an arbitrary direction. Eur. J. Mech. B Fluids,vol.30, pp.236-244.
Chen, P. Y.; Keh, H. J. (2003): Slow motion of a slip spherical particle parallel to one or two plane walls. J. Chin. Inst. Chem. Engrs., vol.34, pp.123-133.
Chen, S. H.; Keh, H. J. (1995): Axisymmetric motion of two spherical particles with slip surfaces. J. Colloid Interface Sci., vol.171, pp.63-72.
Chiu, H. C.; Keh, H. J. (2016): Electrophoresis of a colloidal sphere with double layer polarization in a microtube. Microfluid. Nanofluid., vol. 20, no.64-1-13.
Chiu, H. C.; Keh, H. J. (2017): Diffusiophoresis of a charged particle in a microtube.Electrophoresis, vol.38, pp. 2468-2478.
Churaev, N. V.; Sobolev, V. D.; Somov, A. N. (1984): Slippage of liquids over lyophobic solid surfaces. J. Colloid Interface Sci., vol.97, pp.574-581.
Chwang, A. T.; Wu, T. Y. (1975): Hydrodynamic of low-Reynolds-number flow, Part 2.Singularity method for Stokes flows. J. Fluid Mech., vol.67, pp.787-815.
Dassios, G.; Hadjinicolaou, M.; Payatakes, A.C. (1994): Generalized eigenfunctions and complete semiseparable solutions for Stokes flow in spheroidal coordinates. Quart.Appl. Math., vol.52, pp.157-191.
Deo, S.; Datta, S. (2002): Slip flow past a prolate spheroid. Indian J. Pure Appl. Math. ,vol.33, pp.903-909.
Faltas, M. S.; Saad, E. I. (2011): Stokes flow past an assemblage of slip eccentric spherical particle-in-cell models. Math. Meth. Appl. Sci., vol.34, pp.1594-1605.
Felderhof, B. U. (1977): Hydrodynamic interaction between two spheres. Physica,vol.89A, pp.373-384.
Gluckman, M. J.; Pfeffer, R.; Weinbaum, S. (1971): A new technique for treating multi-particle slow viscous flow: axisymmetric flow past spheres and spheroids. J. Fluid Mech., vol.50, pp.705-740.
Gogte, S.; Vorobieff, P.; Truesdell, R.; Mammoli, A.; van Swol, F.; Shah, P.; Brinker,C. J. (2005): Effective slip on textured superhydrophobic surfaces. Phys. Fluids, vol.17,no.051701, pp.1-4.
Happel, J.; Brenner, H. (1983): Low Reynolds number hydrodynamics. Nijhoff, The Netherlands.
Hornbeck, R. W. (1975): Numerical Methods. Quantum Publishers, New York.
Hu, C. M.; Zwanzig, R. (1974): Rotational friction coefficients for spheroids with the slipping boundary condition. J. Chem. Phys., vol. 60, pp.4354-4357.
Keh, H. J.; Chang, J. H. (1998): Boundary effects on the creeping-flow and thermophoretic motions of an aerosol particle in a spherical cavity. Chem. Eng. Sci.,vol.53, pp.2365-2377.
Keh, H. J.; Chang, Y. C. (2007): Slow motion of a slip spherical particle in a circular cylindrical pore. Int. J. Multiphase Flow, vol.33, pp.726-741.
Keh, H. J.; Chang, Y. C. (2008): Slow motion of a slip spheroid along its axis of revolution. Int. J. Multiphase Flow, vol.34, pp.713-722.
Keh, H. J.; Chang, Y. C. (2010): Slow motion of a general axisymmetric slip particle along its axis of revolution and normal to one or two plane walls. CMES: Computer Modeling in Engineering & Sciences, vol. 62, pp.225-253.
Keh, H. J.; Chen, S. H. (1996): The motion of a slip spherical particle in an arbitrary Stokes flow. Eur. J. Mech., B/Fluids, vol.15, pp.791-807.
Keh, H. J.; Huang, C. H. (2004): Slow motion of axisymmetric slip particles along their axes of revolution. Int. J. Eng. Sci., vol.42, pp.1621-1644.
Keh, H. J.; Lee, T. C. (2010): Axisymmetric creeping motion of a slip spherical particle in a nonconcentric spherical cavity. Theor. Comput. Fluid Dyn., vol.24, pp.497-510.
Keh, H. J.; Shiau, S. C. (2000): Effects of inertia on the slow motion of aerosol particles.Chem. Eng. Sci., vol.42, pp.1621-1644.
Keh, H. J.; Tseng, C. H. (1994): Slow motion of an arbitrary axisymmetric body along its axis of revolution and normal to a plane surface. Int. J. Multiphase Flow, vol.20,pp.185-210.
Lee, T. C.; Keh, H. J. (2013): Slow motion of a spherical particle in a spherical cavity with slip surfaces. Int. J. Eng. Sci., vol.69, pp.1-15.
Lee, T. C.; Keh, H. J. (2014): Electrophoretic motion of a charged particle in a charged cavity. Eur. J. Mech. B/Fluids, vol.46, pp.183-192.
Li, C. Y.; Keh, H. J. (2017): Thermophoresis of a spherical particle in a microtube. J.Aerosol Sci., vol.113, pp.71-84.
Lu, S. Y.; Lee, C. T. (2002): Creeping motion of a spherical aerosol particle in a cylindrical pore. Chem. Eng. Sci., vol.57, pp.1479-1484.
Martini, A.; Roxin, A.; Snurr, R. Q.; Wang, Q.; Lichter, S. (2008): Molecular mechanisms of liquid slip. J. Fluid Mech., vol.600, pp.257-269.
Nir, A. (1976): Linear shear flow past a porous particle. Appl. Sci. Res., vol.32,pp.313-325.
Oberbeck, A. (1876): Uber stationare Flussigkeitsbewegungen mit Berucksichtigung der inner Reibung. J. Reine Angew. Math., vol.81, pp.62-80.
Palaniappan, D. (1994): Creeping flow about a slightly deformed sphere. Z. Angew.Math. Phys., vol.45, pp.832-838.
Payne, L. E.; Pell, W. H. (1960): The Stokes flow problem for a class of axially symmetric bodies. J. Fluid Mech., vol.7, pp.529-549.
Pit, R.; Hervet, H.; Leger, L. (2000): Direct experimental evidence of slip in hexadecane: solid interfaces. Phys. Rev. Lett., vol.85, pp.980-983.
Reed, L. D.; Morrison, F. A. (1974): Particle interactions in viscous flow at small values of Knudsen number. J. Aerosol Sci., vol.5, pp.175-189.
Saffman, P. G. (1971): On the boundary condition at the surface of a porous medium.Studies Appl. Math., vol.50, pp.93-101.
Senchenko, S.; Keh, H. J. (2006): Slipping Stokes flow around a slightly deformed sphere. Phys. Fluids, vol.18, pp.088104-1-4.
Sherif, H. H.; Faltas, M. S.; Saad, E. I. (2008): Slip at the surface of a sphere translating perpendicular to a plane wall in micropolar fluid. Z. Angew. Math. Phys.,vol.59, pp.293-312.
Stokes, G. G. (1851): On the effect of the internal friction of fluid on pendulums. Trans.Cambridge Phil. Soc., vol.9, pp.8-106.
Wan, Y. W.; Keh, H. J. (2009): Slow rotation of an axisymmetric slip particle about its axis of revolution. CMES: Computer Modeling in Engineering & Sciences, vol. 53,pp.73-93.
Wan, Y. W.; Keh, H. J. (2011): Slow rotation of an axially symmetric particle about its axis of revolution normal to one or two plane walls. CMES: Computer Modeling in Engineering & Sciences, vol. 74, pp.109-137.
Yeh, H. Y.; Keh, H. J. (2013): Axisymmetric creeping motion of a prolate particle in a cylindrical pore. Eur. J. Mech. B Fluids, vol.39, pp.52-58.
Ying, R.; Peters M. H. (1991): Interparticle and particle-surface gas dynamic interactions. Aerosol Sci. Technol., vol.14, pp.418-433.
Youngren, G. K.; Acrivos, A. (1975): Stokes flow past a particle of arbitrary shape: a numerical method of solution. J. Fluid Mech., vol.69, pp.377-403.
杂志排行
Computer Modeling In Engineering&Sciences的其它文章
- A Dimension-Reduction Interval Analysis Method for Uncertain Problems
- Computer-Based Modelling of Network Functions for Linear Dynamic Circuits Using Modified Nodal Approach
- Research on Instability Mechanism and Type of Ore Pillar based on the Fold Catastrophe Theory
- Numerical investigation of penetration in Ceramic/Aluminum targets using Smoothed particle hydrodynamics method and presenting a modified analytical model
- An Adaptive Load Stepping Algorithm for Path-Dependent Problems Based on Estimated Convergence Rates
- Performance of Compact Radial Basis Functions in the Direct Interpolation Boundary Element Method for Solving Potential Problems
