A Dimension-Reduction Interval Analysis Method for Uncertain Problems

J.C. Tang and C.M. Fu

1 Introduction

As the uncertainties widely exists in practical engineering problems, such as manufacturing errors, assembly errors and material parameters uncertainties, they may influence the analysis results and design strategies of structures and systems. Therefore, how to appropriately describe those uncertainties has become a significant part of the uncertainty problems.Probability model [Prékopa (1995); Haldar and Mahadevan (2000); Schuëller (2001);Spanos and Brebbia (2012)] is a useful tool to describe uncertainties in structures or systems and gradually becomes the main way to describe uncertainty in practical engineering problems. To establish a probability model, precise probability distribution should be obtained, which acquires abundant samples. However, in practical engineering problems, abundant samples are always difficult to be obtained due to the limitations of experiment conditions and high expenses. Moreover, inadequate samples may cause errors in the probability distribution function and even small errors existed in the probabilistic distribution function may lead to invalid probability analysis result [Ben-Haim and Elishakoff (2013)]. Therefore, it is significant to develop a feasible model which reduces the dependence on the samples to describe the uncertainty. As a result, interval model [Gurav, Goosen and Vankeulen (2005)] emerged as a beneficial supplement to the conventional probability model and gradually been accepted by many researchers and engineers.

Interval model is constructed by upper and lower bounds rather than probabilistic distribution function, thus fewer samples are required to construct interval model comparing to probability model. Afterwards, many interval analysis methods are proposed to calculate the bounds of function response with the uncertain variables described by interval model. The concepts of interval analysis method and interval arithmetic were first proposed by Moore[Moore (1963); Moore, Bierbaum and Schwiertz (1979)], and they were extended to solve the interval finite element problem [Kearfott (1996)]. Interval arithmetic can efficiently calculate the upper and lower bounds of interval function responses. However, the overestimation phenomenon [Neumaier (1993)] hinders the widely use of interval arithmetic in practical engineering problems. In last few decades, many interval analysis methods have been proposed and developed intending to efficiently and precisely calculate the interval function response. Muhanna and Mullen [Muhanna and Mullen (2001)] developed an element by element method to control the overestimation problem in the finite element problem. Dong and shah [Dong and Shah (1987)] proposed a vertex method to calculate interval function responses. Afterwards, the vertex method is employed to many practical engineering problems [Li, Huang and Guo et al. (2010); Qiu, Xia and Yang (2007)]. However,unfortunately, the vertex method is not applicable to the non-monotonic or nonlinear problems, and this method always suffers the “combination explosion” problem, especially in high-dimensional function problems [Khodaparast, Mottershead and Badcock (2011)]. Qiu and Wang [Qiu and Wang (2005)] applied perturbation method [Van Dyke (1964)] and interval arithmetic to evaluate the range of dynamic responses of structures. Chen et al [Chen,Lian, and Yang (2002)] proposed a first order Taylor interval analysis method to calculate uncertain static displacement problem with interval parameters, and it was extended to calculate dynamic response of structures [Chen and Wu (2004)]. Wang et al [Wang, Xiong and Wang et al. (2017); Wang and Wang (2015); Wang, Wang and Li (2016)] proposed a Newton iteration-based interval uncertainty analysis method to analyze the propagating effect of interval uncertainty in multidisciplinary systems, and extended interval analysis method to inverse problems.

Above mention methods allow to obtain interval bounds of response functions, and some of those methods have been important research directions in interval analysis field. However,those interval analysis methods are only limited to problems that the uncertainty level of the interval variables is relatively small. Thus, theoretically, they cannot be used to effectively solve the function responses with a relatively large uncertainty level. Moreover, in practical engineering problems, the variables with a large uncertainty level always existed in structures or systems, such as geometrical sizes of complex structures and systems, external loads. In order to address those mentioned problems, corresponding interval analysis methods with a large uncertainty level are proposed. Chen et al [Chen, Ma and Meng et al. (2009)] proposed an interval decomposition method based on second order Taylor expansion method to calculate the bounds of eigenvalues in structures analysis problems. Fujita and Takewaki[Fujita and Takewaki (2011)] developed two approaches called the fixed reference-point method and the updated reference-point method based on interval decomposition method to calculate interval function responses. The most widely used method is the subinterval method which is proposed by Qiu and Elishakoff [Qiu and Elishakoff (1998)], and this method divides large intervals into subintervals and analyzes all the combinations of subintervals to predict the function response interval. Zhou et al [Zhou, Jiang and Han (2011)] suggested an error estimation method for interval and subinterval analysis methods based on the secondorder truncation error of Taylor expansion, and provided advises for selecting subinterval strategy in large uncertainty level structure problems. Xia and Yu [Xia and Yu (2014)]developed a modified subinterval analysis method to solve the coupled acoustic and structure finite element problems with interval parameters. The results of above papers indicate that the subinterval method is a useful method to solve function interval responses. Wu et al [Wu,Zhang and Chen et al. (2013); Wu, Luo and Zhang et al.(2013)] developed a Chebyshev interval analysis method to reduce or eliminate the overestimation problems of interval arithmetic, and successfully extended this method to ordinary differential equation problems.Manson [Manson (2005)] developed an interval affine method and the key of this method was to decompose interval parameters into several normal intervals according to the coefficients of every two interval parameters. Sofi and Romeo [Sofi and Romeo (2016)]proposed a novel interval finite element method based on the extra unitary interval and applied it to solve linear–elastic structures problem. Xu et al [Xu, Du and Wang et al. (2017)]proposed a dimension-wise analysis method to overcome the potential limitations of overestimation and extended this method to interval structural-acoustic problems.

Overall, the research on interval analysis method of large uncertainty level is still on its primary stage, although there have been some progresses achieved in this field. Solving large interval uncertainty problems is much more complex than solving small uncertainty interval problems. There are two technical problems required to be settle in this area. First, some of interval analysis methods are only suitable to calculate interval response of specific functions.For examples, decomposition method [Chen, Ma and Meng et al. (2009)] was only applicable to monotonic function, because it applied vertex method to calculate interval response.Complex affine analysis method [Manson (2005)]was only suitable for the problems that correlation coefficients between two parameters were already known. More importantly,current large uncertainty interval analysis methods always encounter the low efficiency. Many of existing interval analysis methods suffers low efficiency problems. For examples. The“combination explosion” problem always exists in subinterval analysis method [Qiu and Elishakoff (1998)]. Many function calls are acquired to calculate coefficients of basic functions in Chebyshev interval method, especially in high-dimensional response functions.Therefore, it is crucial to develop an effective and feasible method according to the characteristics of nonlinear functions with relatively large uncertainty level variables.

In order to efficiently calculate lower and upper bounds of a response function with a large uncertainty level, this paper proposes a dimension-reduction interval analysis (DRIA) method.Firstly, the multi-dimensional function is transformed to multi one-dimensional functions by extending dimension-reduction method to interval analysis. Afterwards, second order Taylor expansion method is used to construct standard quadratic form function, based on which interval arithmetic method can be used to calculate interval function responses. The rest of this paper is organized as follows: Section 2 gives the problem statement of interval arithmetic. Section 3 gives the formulation of dimension-reduction interval analysis. Three numerical examples and an engineering application are used to verify the validity of the proposed method in Section 4. Finally, Section 5 gives briefly conclusion of this paper.

2 Problem statement

In most cases, interval response function of nonlinear structure or system can be established as follows [Qiu and Wang (2016)]:

As for the response interval, the upper and lower bounds can be given as:

In practical engineering problem, the response functions can be divided into two kinds:one is the explicit function, and the other is the implicit function. As for an explicit function, the response interval can be directly calculated by interval arithmetic. For two intervals numberfour arithmetic operations are defined as [7, 8]:

And as for an interval number, power function operation is defined as [7, 8]:

Interval function responses can be efficiently calculated by interval arithmetic, but simultaneously the existence of overestimation problem [Andrew (2002)] restricts the widely use of interval arithmetic. Three forms of a response function under an interval variable are used to illustrate the overestimation phenomenon:

Interval arithmetic is also used to calculate interval responses of three forms of a function as follows:

3 Dimension-reduction interval analysis method

It can be observed from the above analyses that interval arithmetic can efficiently calculate the function interval response and the overestimation problem restricts its widely use in practical engineering problems. In this section, a dimension-reduction interval analysis method is proposed to calculate the interval responses of structures or systems. The main strategy of DRIA is to transform the multi-dimensional nonlinear function to standard quadratic function where each variable only occurs once, thus interval power arithmetic can be carried out to calculate the interval response with restricted overestimation. First, dimension-reduction method is extended to the interval analysis problem to transform the multi-dimensional function into several onedimensional functions. Second, standard quadratic function is directly constructed by second order Taylor expansion method. Finally, interval power arithmetic is employed to calculate the interval function response. In general, DRIA method costs few function calls to obtain relatively accurate interval function responses.

3.1 Dimension-reduction interval model

In the stochastic uncertainty analysis problem, the multi-dimensional integrals are used to calculate statistical moments of function response to determine the probabilistic characteristics of random output when input uncertainties are characterized by probability density functions.As for the high dimension function problems, the efficiency to calculate a multi-dimensional integral is relatively low. Therefore, it is significant to develop an efficient integral method.Dimension-reduction integration method [Rahman and Xu (2004); Xu and Rahman (2006);Won, Choi and Choi (2009)] is an efficient probability analysis method to calculate multidimensional integral problems. Based on the level of reduction dimensions, dimensionreduction method can be categorized as univariate dimension-reduction method, bivariate dimension-reduction method and multivariate dimension-reduction method. In this section, only univariate dimension-reduction method is used to construct dimension-reduction function. The key of univariate dimension-reduction method is to transform multi-dimension function into multiple one-dimensional functions as follow:

Eq. (13) indicates that main residual error of dimension-reduction function lie in 4thor higher order, which means that the error of dimension-reduction method is relatively small. In this sense, the integral results obtained by dimension-reduction method is relatively accurate. Thus, this method is widely used in probability analysis problems and related fields [AIAA (2006); Huang, Du and Huang et al. (2006); Wei and Rahman(2007); Lee, Choi, Du and Gorsich (2008); Youn and Xi (2009); Samarbakhsh and Tuszynski (2010); Ristic Gunatilaka and Wang (2017)].

In order to improve the efficiency of interval analysis, dimension-reduction method is extended to interval analysis problem. Dimension-reduction interval function is constructed as:

where Dimension-reduction interval method transforms the multi-dimensional function to multiple one-dimensional functions.It should be noted that interval decomposition method [Chen, Ma and Meng et al. (2009)]can also obtain Eq. (15) by second order Taylor expansion methods. The residual error of the univariate dimension-reduction function can be expressed as:

It can be seen that the residual error of interval dimension reduction functions mainly lies in cross terms.

3.2 Bounds calculation

In order to efficiently calculate the upper and lower bounds of one-dimensional function, second order Taylor expansion method is used in this section to transform one-dimensional functions to standard quadratic functions by which upper and lower bounds of interval function responses can be obtained by interval power arithmetic with controlled overestimation. First, onedimensional functionsare expanded by second order Taylor method as:

Then, Eq. (17) is adjusted to standard quadratic form as:

Substituting Eq. (18) into Eq. (15), dimension-reduction interval function can be formulated as:

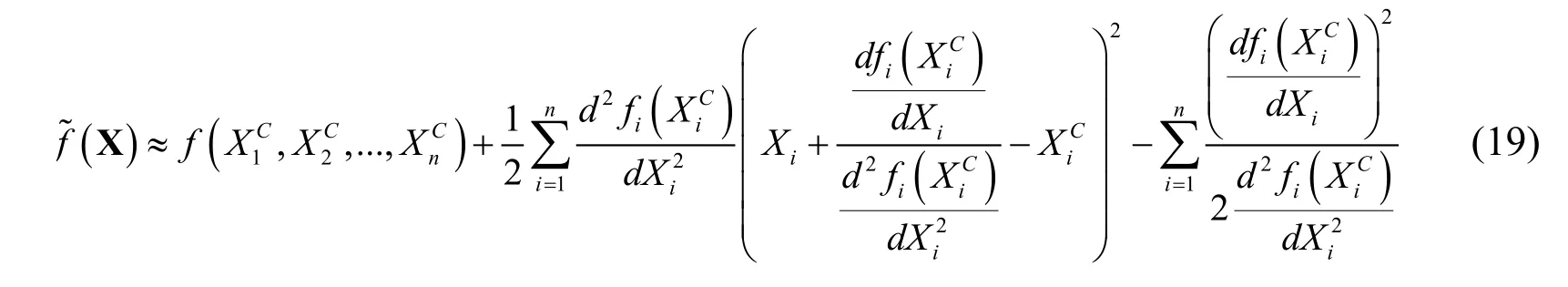
It is can be seen from Eq. (20) that each interval only occurs once, therefore interval power function [Moore (1963); Moore, Bierbaum and Schwiertz (1979)] can be employed to calculate the upper and lower bounds. The power function of i-th variablecan be solved by interval power operation as follows:

Comparing with first order Taylor expansion, DRIA considers second-order term of onedimensional functions. Thus, DRIA will be more applicable to nonlinear functions.Moreover, Dimension-reduction interval analysis method only needs the first order derivative and second order derivative of one-dimensional functions. As for the explicit function, those derivatives can be obtained by derivation, and as for implicit function those derivatives can be easily obtained by forward difference, backward difference or central difference method. In this paper, central difference method is selected to calculate the derivatives, and the first order and second order derivatives of the i-th onedimensional function can be obtained as follows:

Table 1: The function calls of interval analysis methods

4 Examples

In this section, four nonlinear examples including three numerical examples and an engineering application are used to demonstrate the validity of DRIA. The results obtained by Sequential Quadratic Program (SQP) optimization method [Gill, Murray and Saunders (2006)] are selected as reference solutions to verify the accuracy of DRIA.Moreover, first order Taylor expansion interval method [Chen, Lian, and Yang (2002)]and Chebyshev interval method [Wu, Zhang and Chen et al. (2013); Wu, Luo and Zhang et al.(2013)] are employed to predict upper and lower bounds of function responses for comparing to the results obtained by DRIA method. In all examples, central difference method is used to calculate function derivatives. In Chebyshev interval method, the order of Chebyshev polynomial expansion model is selected to be 3. The larger relative error between upper bound and lower bound is called larger relative error.

4.1 Example 1

Consider the two dimensions nonlinear response function:

While the uncertainty levels increase to 30%, interval variables are expanded to. The relative errors of lower bound and upper bound obtained by DRIA method are 2.81% and 6.20%, respectively. The relative error of lower bound obtained by Chebyshev interval method reaches to 24.04% and the relative error of upper bound obtained by first order Taylor expansion method reaches to 23.49%. While the uncertainty levels increase to 40%, interval variables are expanded toThe relative errors obtained by DRIA is 4.16%and 14.35%. The relative errors obtained by first order expansion are 25.45% and 37.47%.The relative errors obtained Chebyshev method are 40.26% and 3.84%, respectively. It reflects that DRIA method has better performance comparing to other two interval analysis methods at relatively large uncertainty level of 40%.

As shown in Fig. 1, the larger relative error obtained by three methods at the four uncertainty levels are depicted. It can be seen that larger relative errors of all the interval analysis methods increase with the increasing uncertainty level of interval variables.Among the three interval analysis methods, the larger relative errors obtained by Chebyshev interval method are larger than first order Taylor interval method and the proposed method. The larger relative errors obtained by first order Taylor method are near those obtained by Chebyshev method, and the larger relative errors obtained by proposed method are relatively lower than others two interval analysis methods. Based on the results, It can be concluded that DRIA method have good performance both in efficiency and accuracy compared with other two interval analysis methods at the four uncertainty levels.

Table 2: The function calls and relative errors obtained by three interval analysis at four different uncertainty levels

Figure 1: The larger bound errors of three interval analysis methods with increasing uncertainty levels

4.2 Example 2

Consider the follow response function with ten interval variables:

where the midpoints of all the interval variables are set to be 3, and the uncertainty levels are 50%，20%，20%，20%，20%，40%，30%，10%，10% and 10%, respectively.Table 3 shows the computing results of three interval analysis methods, the relative errors obtained by DRIA are 0.61% and 5.02% by 21 function calls. With the same function calls as DRIA method, the relative errors of first order Taylor expansion method reach to 38.41% and 14.72%. As for the Chebyshev interval method, it should be noted that in addition to 59049 function calls, Chebyshev interval method still need a large number of trigonometric function calls which is too time-consuming. In accuracy aspect, the results obtained by Chebyshev method are compared to the reference ones, and the relative error of lower bound is reach to 55.94%. Those results indicate that DRIA have good performance both in efficiency and accuracy for high-dimensional functions with larger uncertainty interval variables.

Table 3: The interval responses calculated by interval analysis methods in example 2

4.3 Example 3

A rotating disk [Chowdhury and Rao (2009)] is subjected to a relative fast angular velocityas shown in Fig. 2. The safety margin before an overstress condition occurs due to the stress on the part being too large for the material to withstand is defined as burst margin:

Figure 2: The rotating disk

Table 4: The midpoints and uncertainty levels of interval variables in rotating disk model

Table 5: The interval responses and relative errors obtained by three interval analysis methods in rotating disk model

4.4 Application to electronic wearable system of a smart watch

In this example, the proposed method is applied to an electronic wearable system of a smart watch as shown in Fig. 3. The thicknesses and Yong’s Modulus are interval uncertainty variables as shown in Table 6. In order to ensure the reliability of this watch,we choose one point on the screen as an experiment point to hit against with a steel ball.During the simulation test, maximum stressof the screen should not be higher than the allowable value. As shown in the Fig. 4, the FEM model is established to computer the performance function of maximum stress based on recent work [Huang, Jiang and Zhou et al. (2016)]. In order to improve computational efficiency, a quadratic response surface model is constructed by 65 FEM samples:

Three interval analysis methods are applied to calculate upper and lower bounds of the quadratic response function. As shown in Table 7, the relative errors obtained by DRIA method are 4.86% and 5.58%, and the relative errors obtained by first order Taylor interval method reach up to 72.47% and 9.47% by 13 function calls. The relative errors obtained by Chebyshev interval method reach to 47.57% and 21.01% by 486 function calls. Comparing with other two interval analysis methods, DRIA method is relatively efficient and accurate in this application.

Figure 3: The smart watch

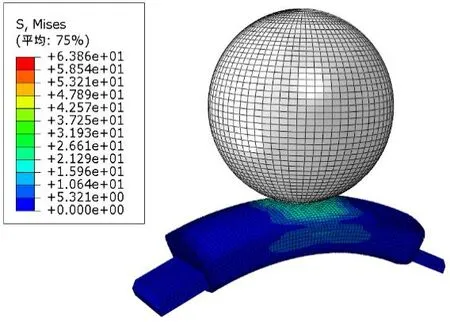
Figure 4: FEM model of the smart watch

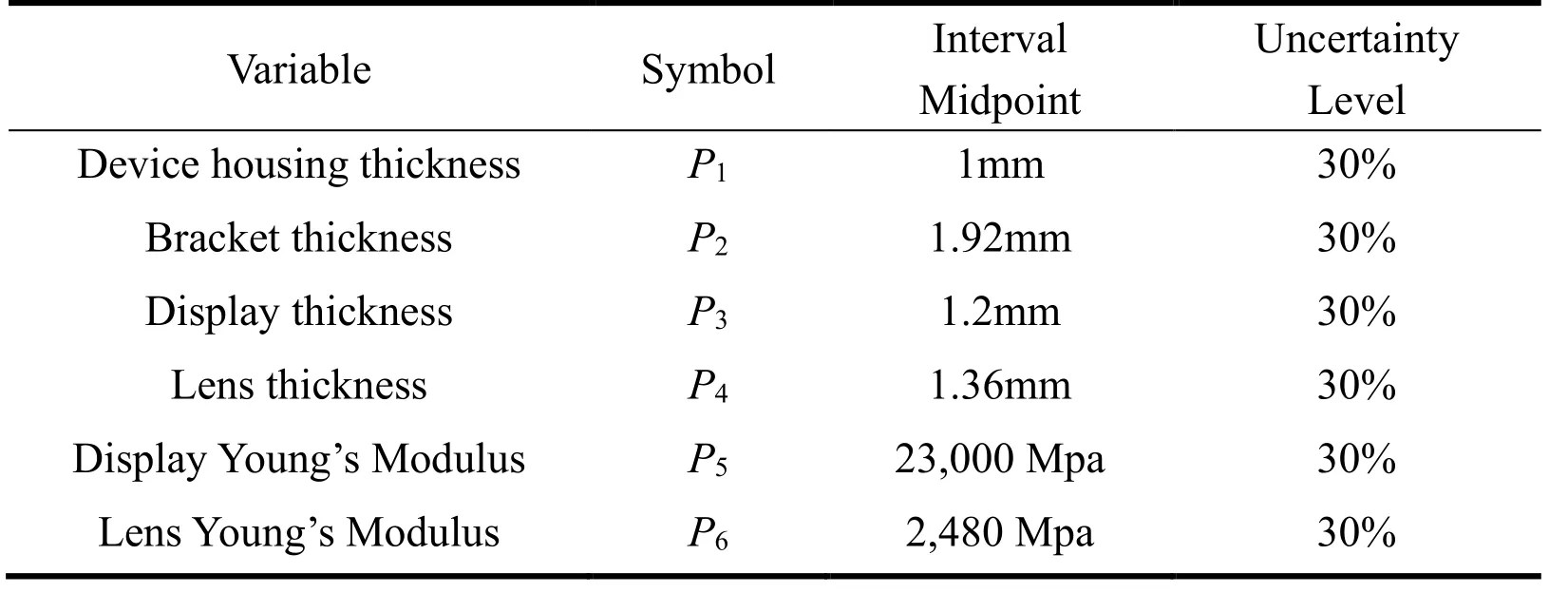
Table 6: The interval midpoint and uncertainty levels information in smart watch

Table 7: The interval responses calculated by interval analysis methods in smart watch

5 Conclusions

In this paper, a new interval method called dimension-reduction interval method (DRIA)is proposed to predict the interval responses of nonlinear structures or systems with interval variables. The key of this method is to transform a multi-dimensional function to a standard quadratic function, in which each variable is adjusted to appear only once. As a result, interval power arithmetic can be used to calculate interval response with controlled overestimation. DRIA method is compared with other two interval analysis methods. Through analyzing the results of four examples, it is found that the results obtained by DRIA method are very close to the ones of the SQP; the efficiency is as high as first order Taylor expansion interval method; the relative errors of computing results are smaller than the first order Taylor expansion interval method and Chebyshev interval method. Especially in example 3, the larger error obtained by the proposed method can be controlled within 10%, while first order Taylor expansion interval method and Chebyshev interval analysis method are 42.86% and 85.71% respectively. However, due to the shortness of dimension-reduction function, the result accuracy obtained by DRIA may decrease when dealing with the functions that cross terms have strong influences.Therefore, in the future, we will focus on this shortness and update DRIA method.

Andrew, A. M. (2012): Applied Interval Analysis: With Examples in Parameter a nd State Estimation, Robust Control and Robotics. KYBERNETES, vol. 31, no. 5,pp.117-123.

Chen, S.; Lian, H.; Yang, X. (2002): Interval static displacement analysis for structures with interval parameters. INT J NUMER METH ENG, vol. 53, no. 2, pp. 393-407.

Chen, S. H.; Ma, L.; Meng, G. W.; Guo, R. (2009): An efficient method for evaluating the natural frequencies of structures with uncertain-but-bounded parameters. COMPUT STRUCT, vol. 87, no. 9-10, pp. 582-590.

Chowdhury, R.; Rao, B. N. (2009): Assessment of high dimensional model repre sentation techniques for reliability analysis. PROBABILIST ENG MECH, vol. 24, n o.1, pp.100-115.

Chen, S. H.; Wu, J. (2004): Interval optimization of dynamic response for structures with interval parameters. COMPUT STRUCT, vol. 82, no. 1, pp. 1-11.

Dong, W.; Shah, H. C. (1987): Vertex method for computing functions of fuzzy variables. Fuzzy Sets & Systems, vol. 24, no. 1, pp. 65-78.

Fujita, K.; Takewaki, I. (2011): An efficient methodology for robustness evaluation by advanced interval analysis using updated second-order Taylor series expansion. ENG STRUCT, vol. 33, no. 12, pp. 3299-3310.

Gurav, S. P.; Goosen, J. F. L.; Vankeulen, F. (2005): Bounded-But-Unknown uncertainty optimization using design sensitivities and parallel computing: Application to MEMS. COMPUT STRUCT, vol. 83, no. 14, pp. 1134-1149.

Gill, P. E.; Murray, W.; Saunders, M. A. (2006): An SQP algorithm for large-scale constrained optimization. SIAM J OPTIMIZ, vol. 12, no. 4, pp. 979-1006.

Huang, B.; Du, X.; Huang, B.; Du, X. (2006): Uncertainty Analysis by Dimension Reduction Integration and Saddlepoint Approximations. J MECH DESIGN, vol. 128, no.1, pp. 1143-1152.

Huang, Z. L.; Jiang, C.; Zhou, Y. S.; Luo, Z.; Zhang, Z. (2016): An incremental shi fting vector approach for reliability-based design optimization. STRUCT MULTIDISCIP O, vol. 5, no. 3, pp. 522-543.

Kearfott, R. B. (1996): Interval computations: introduction, uses and resources. Euromath Bulletin, vol. 219 no. 96, pp. 95-112.

Khodaparast, H. H.; Mottershead, J. E.; Badcock, K. J. (2011): Interval model updating with irreducible uncertainty using the Kriging predictor. Mechanical Systems &Signal Processing, vol. 25, no. 4, pp. 1204-1226.

Lee, I.; Choi, K. K.; Du, L.; Gorsich, D. (2008): Inverse analysis method using MPP-based dimension reduction for reliability-based design optimization of nonlinear and multi-dimensional systems. Computer Methods in Applied Mechanics & Engineering, vol.198, no. 1, pp. 14-27.

Li, Y. P.; Huang, G. H.; Guo, P.; Yang, Z. F.; Nie, S. L. (2010): A dual-interval vertex analysis method and its application to environmental decision making under uncertainty.EUR J OPER RES, vol. 200, no. 2, pp. 536-550.

Manson, G. (2005): Calculating frequency response functions for uncertain system s using complex affine analysis. Journal of Sound & Vibration, vol. 288, no. 3, p p. 487-521.

Moore, R. E. (1963): Interval arithmetic and automatic error analysis in digital computing. Stanford University.

Moore, R. E.; Bierbaum, F.; Schwiertz, K. (1979): Methods and applications of interval analysis. SIAM,

Muhanna, R. L.; Mullen, R. L. (2001): Uncertainty in mechanics problems-Interv al-Based Approach. J ENG MECH, vol. 127, no. 6, 557-566.

Neumaier, A. (1993): The wrapping effect, ellipsoid arithmetic, stability and confidence regions. Springer Vienna.

Prékopa, A. (1995): Stochastic Programming. Springer Netherlands.

Qiu, Z.; Elishakoff, I. (1998): Antioptimization of structures with large uncertainbut-non-random parameters via interval analysis. Computer Methods in Applied Me chanics & Engineering, vol.152, no.3-4, pp.361-372.

Qiu, Z.; Xia, Y.; Yang, J. (2007): The static displacement and the stress analysis of structures with bounded uncertainties using the vertex solution theorem. Computer Methods in Applied Mechanics & Engineering, vol. 196, no. 49, pp. 4965-4984.

Qiu, Z.; Wang, X. (2005): Parameter perturbation method for dynamic responses of structures with uncertain-but-bounded parameters based on interval analysis. International Journal of Solids & Structures, vol. 42, no. 18, pp. 4958-4970.

Qiu, Z. P; Wang, L. (2016): The need for introduction of non-probabilistic interval conceptions into structural analysis and design. Science China Physics Mechanics &Astronomy, vol. 59, no. 11, pp. 114632.

Ristic, B.; Gunatilaka, A.; Wang, Y. (2017): Rao–Blackwell dimension reduction applied to hazardous source parameter estimation. SIGNAL PROCESS, vol.13, no.2, pp. 177-182.

Rahman, S.; Xu, H. (2004): A univariate dimension-reduction method for multi-di mensional integration in stochastic mechanics. PROBABILIST ENG MECH, vol. 21,no. 4, pp. 393-408.

Schuëller, G. I. (2001): Computational stochastic mechanics-recent advances. COMPUT STRUCT, vol. 79, no. 22–25, pp. 2225-2234.

Spanos, P. D.; Brebbia, C. A. (2012): Computational stochastic mechanics. Springer Science & Business Media.

Sofi, A.; Romeo, E. (2016): A novel Interval Finite Element Method based on the improved interval analysis. Computer Methods in Applied Mechanics & Engineering, vol.3, no. 11, pp. 671-697.

Samarbakhsh, A.; Tuszynski, J. (2010): Bayesian Approach for Structural Reliability Analysis and Optimization Using the Kriging Dimension Reduction Method. J MECH DESIGN, vol. 132, no. 5, pp. 51003.

Van Dyke, M. (1964): Perturbation Methods in Fluid Mechanics. Academic Press.

Won, J.; Choi, C.; Choi, J. (2009): Improved dimension reduction method (DRM) in uncertainty analysis using kriging interpolation. J MECH SCI TECHNOL, vol. 23, no. 5,pp. 1249-1260.

Wu, J.; Luo, Z.; Zhang, Y.; Zhang, N.; Chen, L. (2013): Interval uncertain method for multibody mechanical systems using Chebyshev inclusion functions. INT J NUMER METH ENG, vol. 95, no. 7, pp. 608-630.

Wei, D.; Rahman, S. (2007): Structural reliability analysis by univariate decomposition and numerical integration. PROBABILIST ENG MECH, vol. 22, no. 1, pp. 27-38.

Wang, L; Wang, X. (2015): Dynamic loads identification in presence of unknown but bounded measurement errors. Inverse Problems in Science & Engineering, vol. 23, no. 8,pp. 1313-1341.

Wang, L.; Wang, X; Li, X (2016): Inverse system method for dynamic loads identification via noisy measured dynamic responses. ENG COMPUTATION, vol. 33, no.4, pp. 1070-1094.

Wang, L.; Xiong, C.; Wang, R. X.; Wang, X. J.; Wu, D. (2017): A novel method of Newton iteration-based interval analysis for multidisciplinary systems. Science China Physics Mechanics & Astronomy, vol. 60, no. 9, pp. 94611.

Wu, J.; Zhang, Y.; Chen, L; Luo, Z. (2013): A Chebyshev interval method for nonlinear dynamic systems under uncertainty. APPL MATH MODEL, vol. 37, no.37, pp. 4578-4591.

Xia, B.; Yu, D. (2014): Modified interval and subinterval perturbation methods for the static response analysis of structures with interval parameters. J STRUCT ENG, vol. 140,no. 5, pp. 155-164.

Xu, M.; Du, J.; Wang, C.; Li, Y. (2017): A dimension-wise analysis method for the structural-acoustic system with interval parameters. Journal of Sound & Vibration, vol. 3,no. 94, pp. 418-433.

Xu, H.; Rahman, S. (2006): A generalized dimension‐reduction method for multi‐dim ensional integration in stochastic mechanics (Int. J. Numer. Meth. Engng 2004; 61:1992–2019). INT. J. NUMER METH ENG., vol. 65, no. 13, pp. 2292.

Youn, B. D.; Xi, Z. (2009): Reliability-based robust design optimization using the eigenvector dimension reduction (EDR) method. Structural & Multidisciplinary Optimization, vol. 37, no. 5,pp. 475-492.

Zhou, Y.; Jiang, C.; Han, X. Interval and subinterval analysis method of the structure analysis and their estimation. INT J COMP METH-SING, vol. 03, no. 2, pp. 229-244.