An Adaptive Load Stepping Algorithm for Path-Dependent Problems Based on Estimated Convergence Rates

M.T.C. Araújo Fernandes, C.O. Cardoso and W.J. Mansur

1 Introduction

In nonlinear finite element modelling, the use of robust and efficient solution algorithms is a fundamental step for the success of a reliable analysis. The main purpose of these algorithms is to solve a set of nonlinear algebraic equations. The solution algorithms are efficient when besides being reliable, the computational cost and the analyst effort are relatively low. In order to improve these two characteristics, robust adaptive solution algorithms are continuously presented in the literature [Bathe and Dvorkin (1983)].

Nonlinear structural problems solved by numerical algorithms may have multiple solutions (analyses with snap-through or snap-back buckling) or be path-dependent(analyses with material nonlinearities) [Bergan et al (1978)].

Different load incrementation strategies and parameters to define the increment size have been continuously developed to solve the aforementioned problems. Some of these strategies are: the current stiffness parameter [Bergan et al (1978)], the length of the equilibrium path [Riks (1979)], arc-length techniques [Crisfield (1981)], incremental schemes with error control [Abbo and Sloan (1996)] and scalar homotopy methods[Elgohary et al (2014)]. Other algorithms can be found in references [Schweizerhof and Wriggers (1986); Geers (1999); Sheng, Sloan and Yu (2000); Sheng and Sloan (2003);Ritto-Corrêa and Camotim (2008); Stull, Earls and Aquino (2008); Sheng, Nazem and Carter (2009); Lindgaard and Lund (2010); Labeas and Belesis (2011); Koohestani(2013); Hardyniec and Chraney (2015)].

However, in order to ensure robustness, the traditional arc-length method and its variations have complex implementations that include the monitoring of the eigenvalues of the Jacobian matrices and the use of additional constraint equations [Abbo and Sloan(1996); Elgohary et al (2014)]. For these reasons, the development of robust and simple to implement algorithms to solve nonlinear structural problems is still in progress.

In this paper, the path-dependent problems are treated in some detail. Fig.1, which shows a typical load displacement curve where it can be seen a drastic reduction on stiffness for the limit load, illustrates the degree of difficulty one may face when solving these kinds of problem.

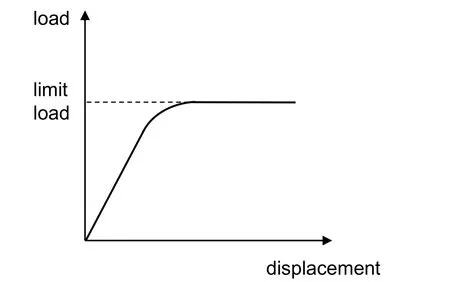
Figure 1: Limit load analysis considering material nonlinearity.

In this case, usual procedures to obtain the limit load, require the total external load to be divided into increments and the accuracy of the finite element solution is dependent of the size of each increment.

Additionally, in plasticity theory, infinitesimal deformations are considered and depending on the size of the chosen load increments, the calculation of displacements,strains and stresses can have significant errors. Therefore, one may be tempted to choose excessively small load increments, and pay the price: the analysis becomes too expensive,in some cases impossible to deal with when one has deadlines, or else one must abandon a desktop working station and use supercomputers. Thus, one must be aware when designing adaptive load stepping algorithms to analyze nonlinear problems that the size of the load increments can vary substantially during the analysis without accuracy loss.

Taking into account the above considerations, a new adaptive load stepping algorithm based on the estimated convergence rate of the nonlinear iterative process is presented.The algorithm is used together with the full Newton-Raphson method to solve the nonlinear finite element equations.

The convergence rate was considered as the control variable of the adaptive process due to its mathematical definition, which guarantees the robustness of the algorithm and was calculated based on a force norm during the incremental load process.

The new adaptive load stepping algorithm, the RCA (Rate of Convergence Algorithm)algorithm has been firstly applied to solve nonlinear elastoplastic problems. The RCA algorithm has been implemented in the in-house 2D and 3D finite element program AMG(Mechanical and Geomechanical Analysis) [Costa (1984); Cardoso (2005)]. Static and dynamic analyses with material and geometric nonlinearities can be performed by AMG.In the next section a brief discussion about the convergence rate of nonlinear iterative processes is presented. An estimation of the convergence rate for computational implementation is also discussed [Gustafsson and Soderlind (1997)]. The RCA algorithm is presented in Section 3. The solutions obtained with AMG/RCA are discussed in Section 4 and compared with the FEA commercial software ABAQUS® [Abaqus (2012)]. Finally, in Section 5, concluding remarks are drawn.

2 Rate of convergence of iterative processes

Firstly, the formal definition of the convergence rate of a general iterative process is given.

exists, and asymptotically the following equality is true:

At this point the following remarks are due:

1) In the full Newton-Raphson method, which is adopted in this paper, the quadratic order of convergence is not usually achieved in elasto-plastic problems. This occurs because the Jacobian matrix is not continuously differentiable when an element quadrature point changes its state from elastic to plastic or from plastic to elastic [Belytschko, Liu and Moran(2000)];

2) Commonly, iterative processes have three phases: nonlinear transient, linear transient and finally asymptotic [Gustafsson and Soderlind (1997)];3) In an iterative process, the rate of convergencewill only be representative if a considerable number of iterations have been performed, i.e., the asymptotic phase has been achieved.

In order to present the estimated convergence rate used in this paper, it is necessary to def ine the nonlinear algebraic equations (equilibrium equations) for nonlinear structural prob lems:

The estimated convergence ratepresented in this paper is a modification of the rate ba sed on vector norms presented in [Gustafsson and Soderlind (1997)]. Taking into account the equilibrium equations of nonlinear problems in an incremental notation, the new prop osed estimative foris given by:

where

Diverging increments can be detected using Eq. 5. This situation occurs when values ofare negative oris positive andIn both cases, the force norms and consequently the force residuals are not decreasing.

Generally, large positive values ofindicate a fast convergence of the iterative process.In other words, ifwill tend to infinity.

Similarly, small positive values ofindicate a slow convergence of the iterative proces s. In other words, ifwill tend to zero.

The idea behind Eq. 5 is to link the history of values of the variable, with the speed of convergence of the current load increment that will be used to calculate the size of the ne xt load increment.

3 Adaptive load stepping algorithms based on convergence rate

In this section, the new automatic load stepping algorithm, the RCA, is presented.Initially, it is necessary to define the incremental finite element equations that describe the response of a nonlinear structure in a static analysis due to a varying load:

The iterative process ends when the force norm (Eq. 6) and the displacement norm (Eq.9), are smaller than specified tolerances.

After the convergence check, the current load increment will be accepted or not. In both situations, the main objective of an adaptive load stepping algorithm is to define suitable load factorsfor each load increment based on the estimated convergence rate.

The speed of convergence of the incremental/iterative solution of Eq. 7 is related to the average values ofof each load increment. The average value is calledand is calculated at the end of each load increment.

The speed of convergence is classified as fast, constant or slow and grouped in regions(Fig.2). The definition of these convergence regions is based on statistical analysis of the valuesperformed in different analyses.

Fig.2 schematically shows how the different speeds of convergence are correlated with the values of.

Figure 2: Graphical representation of the speed regions and correlation with . Full circles represent punctual values of iterations for one load increment.

Regarding Fig. 2, the different regions are limited by thevalues. At the end of the convergence process, four different situations are considered in the algorithm:a) A load increment is classified as fast if(Eq. 14) is located in the fast region and if the maximum number allowed for iterations in the slow regionhas not been reached. In this case, the next load increment is increased by a factor

b) A load increment is classified as constant ifis located in the constant region and if the maximum number allowed for iterations in the slow region () has not been achieved. In this case, the next load increment remains constant:

c) A load increment is classified as slow ifis located in the slow region or if the maximum number allowed for iterations in the slow regionhas been achieved.In this case, the next load increment is decreased by a factor

d) Finally, a load increment is classified as divergent if a certain number of iterations,defined by user, with values oflocated in the divergence region has been achievedIn this case the load step is restarted and the load increment is decreased by a factor

Still regarding the parameters of the algorithm, if the load step is too small, the computational cost of the analysis can be very high. On the other hand, a large load step can lead either to non-convergence or to a great number of iterations to achieve equilibrium. For this reason, a maximum value formust be set to avoid a very large load increment in linear or nearly linear regions of the load path. Similarly, in order to stop the analysis and to prevent unnecessary calculations, a minimum value forshould also be defined.

Finally, the incremental procedure ends when the entire load is applied:

4 Applications

The elastoplastic analyses described next were performed with fixed and automatic load step incrementation (RCA algorithm). In the analyses with the RCA algorithm, the most critical parameter isFor this reason, different values ofwere tested. The results obtained with AMG/RCA were also compared with those by the FEA commercial software ABAQUS®.

4.1 Collapse of an end-loaded cantilever beam

The plastic collapse of an end-load cantilever beam is studied in the first example [Souza Neto, Peric and Owen (2008)]. Fig. 3 shows the cross-section, boundary conditions and applied load. Tab. 1 presents the parameters of the model.

Figure 3: Geometry of the end-loaded cantilever beam.

Table 1: Parameters of the end-loaded cantilever beam model.

The beam material is elastoplastic and represented by von Mises yield surface with isotropic hardening and plane stress state (Tab. 2).

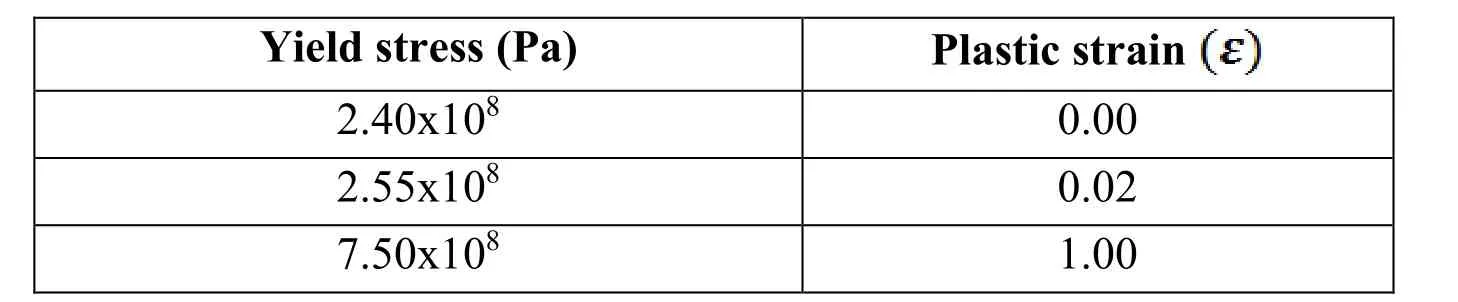
Table 2: Stress-strain data for isotropic hardening rule adopted.

One hundred sixty quadrilateral elements with eight nodes were used (forty elements along the length and four along the height) employing four (2x2) Gauss quadrature points.The tolerance for displacement and force residuals was set to 10-3.

For the analyses with fixed load steps, one hundred load increments of 0.4 kN were applied until reach the maximum collapse load.

Tab. 3 summarizes the parameters adopted in the RCA algorithm for the end-loaded cantilever beam.

Table 3: Parameters of the RCA algorithm.

The initial load step of the automatic analyses (AMG/RCA and ABAQUS®) was set to 0.01.

In the automatic analysis performed with ABAQUS®, the maximum load step was set to, associated with the default solver controls and full Newton-Raphson method.

Tab. 4 presents the number of load increments and collapse loads for different values ofThe objective is to evaluate the performance of the AMG/RCA algorithm and to compare it with the load increment history path obtained with ABAQUS®. The variableis the maximum collapse load calculated by the algorithms.

Table 4: Results for the end-loaded cantilever beam.

According to Tab. 4, the total number of load increments of AMG/RCA analyses is highly dependent of theparameter. In all AMG/RCA automatic analyses, a smaller number of load increments was necessary in comparison with the AMG fixed load step analysis.

The ABAQUS® analysis presented a number of load increments similar to the AMG/RC A analysis with

Fig. 4 shows the distribution of different types of iterations according to the speed regions giving a better understanding of the numerical computational effort.

Figure 4: Distribution of the iterations according to the speed regions.

In the analyses with reduced number of load increments,the percentage of iterations located in the constant region are the highest among all the analyses. It means that the increment size does not change unnecessarily during the analysis.

Fig. 5 gives the variation of the load factorsplotted for different automatic analyses in order to illustrate the previous statement.

Figure 5: Variation of the load factors for different values of .

Figure 6: Load-displacement curves of the end-loaded cantilever beam.

As it can be seen in Fig. 6, AMG/RCA successfully adjusted the increment size during the nonlinear stage of the analysis in a consistent way with ABAQUS®.

Finally, Fig. 7 shows the accumulative frequency history offor different values ofused to calibrate speed regions.

Figure 7: Histograms for the variable in different automatic analyses, showing speed regions for different values of .

Despite some minor differences in the initial tail (λslow＜0.0), the histograms showed a similar behavior for different values ofThe similar behavior of the histograms shows that the main difference between the analyses, in terms of the number of load increments, is related to the definition of the speed regions. As explained before, the analyses with reduced number of load increments have the highest proportion of constant iterations. If the constant region is not correctly defined by the values ofmore iterations are unnecessarily classified as slow or fast. In the analysis with for example, a large percentage ofvalues are in the slow regions andmore iterations are classified as slow. The load steps are successively diminished,increasing the nu mber of increments required to perform the analysis (see Fig. 5). On the other hand, forthe constant region is more adequately defined,requiring less increments to perform the analyses.

4.2 Strip-footing collapse

The bearing capacity of a rigid strip footing is analyzed using fixed load increments,AMG/RCA and compared with FEA commercial software ABAQUS®. Fig. 8 gives the geometry of the problem.

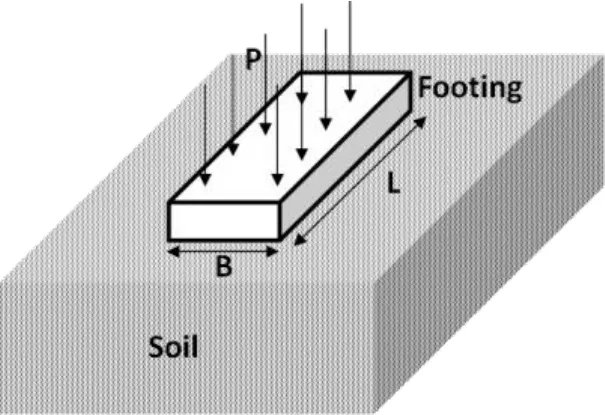
Figure 8: Geometry of the rigid strip-footing.

Table 5: Parameters of the rigid strip-footing model.

Fig. 9 shows the adopted mesh, comprised of 3697 nodes and 1184 eight-noded quadrilaterals elements with four (2x2) Gauss quadrature points.

Figure 9: Finite element mesh of rigid the strip-footting.

The tolerance for displacement and force residuals was set to 10-3.

For the analyses with fixed load step, one hundred load increments of 6.0x10-4m were applied. The average pressure p is calculated dividing the total reaction on the footing by the width B.

The adopted parameters of the RCA algorithm are shown in Tab. 6.

Table 6: Parameters of the RCA algorithm.

The initial load step of the automatic analyses (AMG/RCA and ABAQUS®) was set to 0.01.In the automatic analysis performed with ABAQUS®, the maximumload step was set to 0.05 associated with the default solver controls and full Newton-Raphson method.

Tab. 7 presents the number of load increments and collapse pressures. The variable “”is the maximum pressure calculated in the algorithm and “ ” is the limit pressure predicted by Terzaghi´s solution [Lambe and Whitman (1979)].

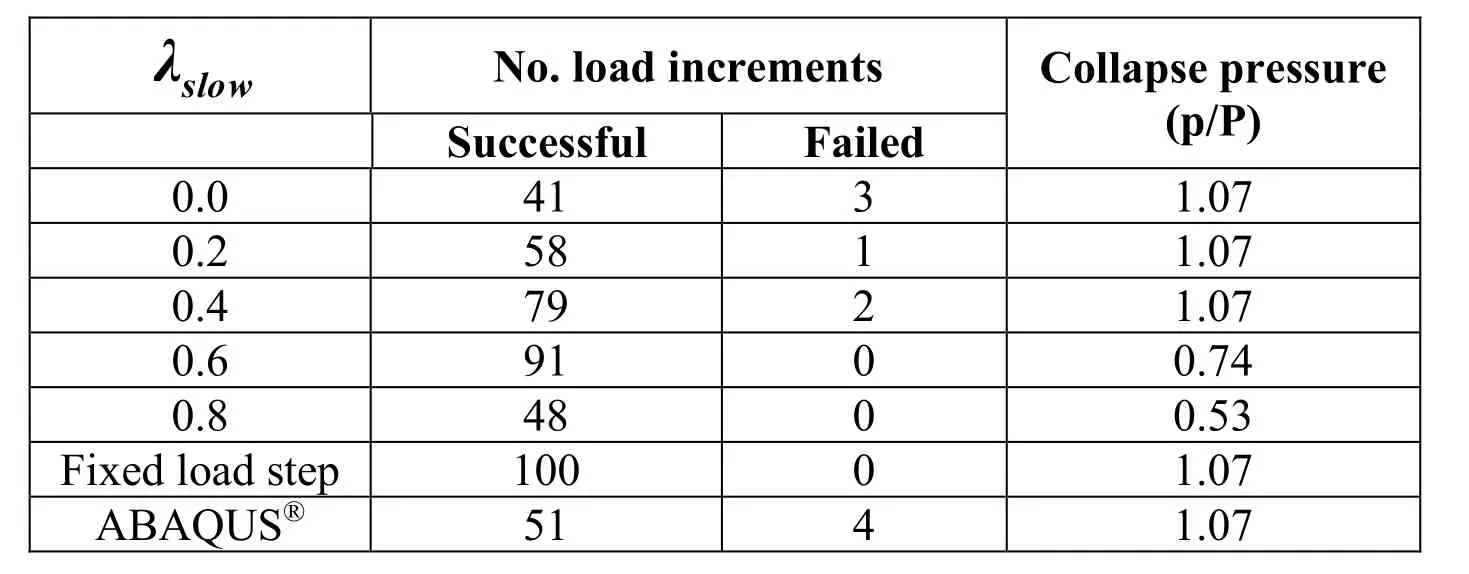
Table 7: Results for the rigid strip-foundation.

Similar to the first example, for all automatic analyses, the number of load increments showed dependence on λslowand a smaller number of load increments was necessary in comparison with the fixed load step analysis.

The relatively small number of increments for λslow=0.8is explained by the early interruption of this analysis, as it can be seen in Tab.7 by the low value of pressure obtained.

The analysis with AMG/RCA presented an improved performance in comparison with ABAQUS® in the analysis with λslow=0.0. For this case, the number of load increments in AMG/RCA represents 80% of the number of load increments obtained with ABAQUS® for the same collapse pressure.

Fig. 10 gives the distribution of different types of iterations from the AMG/RCA versus the parameter λslow.

Figure 10: Distribution of the iterations accordingly to the speed regions.

The higher percentage of iterations classified in the region with constant speed of conver gence is associated with the reduced number of load increments, similarly to the cantileve r beam example. The small discrepancy presented in the analysis with λslow=0.8is expl ained by the early interruption of this analysis.

The variation of load factors Δδplotted for the AMG/RCA automatic analyses (Fig. 11),also shows that the best performances in terms of number of load increments are obtained with λslow=0.0and 0.2, in these cases the load factors do not change frequently during the analysis compared with the higher values of λslowtested.

Figure 11: Variation of the load factors for different values of λslow.

Fig. 12 shows the pressure-displacement curves for AMG fixed step, AMG/RCA withABAQUS® with automatic step and Terzaghi’s analytical solution [Lambe and Whitman (1979)].

Figure 12: Pressure-displacement curves of the rigid strip-footing problem.

The AMG/RCA with λslow=0.0was able to adjust the load increment size close to the limit load with less effort than ABAQUS® (see Tab.7). The limit pressure calculated in all different numerical analyses, have a good match reaching values close to the Terzaghi’s analytical solution.

Fig. 13 gives the accumulative frequency history offor different values of.

Figure 13: Histograms for the variable λkin different automatic analyses.

The histograms presented in Fig. 13, show a similar behavior observed in the cantilever beam example for different values of λslow. The values of λslowand λfastconsidered suitable for application in the solution of a large number of nonlinear analyses with reduced number of load increments, must present a high proportion of constant iterations to optimize the automatic load incrementation process.

5 Concluding remarks

The objective of this paper is to show a new algorithm, called RCA, based on the estimated convergence rate of a nonlinear iterative process. The algorithm is relatively simple to implement, robust and presents a better performance when compared with fixed load step approaches. The performance of the RCA algorithm in the analysis of the rigid strip-footting presented here had also a better performance than the load incrementation algorithm of the FEA commercial software ABAQUS®.

Through the study of the histograms of the estimated convergence rate, it was possible to calibrate a set of parameters of the algorithm to be used in different nonlinear analyses.

Although the RCA algorithm was successfully employed in path-dependent nonlinear problems, it can also be used for different types of nonlinearities due its robustness ensured by the generality of the estimation of the convergence rate.

Acknowledgement: The authors wish to thank Petrobras and the Brazilian research funding agencies CNPq, FAPERJ and CAPES for their support to this work.

ABAQUS, Inc. (2012): Version 6.12-3, Providence, RI 02909–2499.

Abbo, A. J.; Sloan, S. W. (1996): An automatic load stepping algorithm with error contr ol. International Journal for Numerical Methods in Engineering, vol. 39, pp. 1737-1759.Bathe, K. J.; Dvorkin, E. N. (1983): On the automatic solution of nonlinear finite eleme nt equations. Computers & Structures, vol. 17, pp. 871-879.

Belytschko, T.; Liu, W. K.; Moran, B. (2000): Nonlinear finite elements for continua a nd structures. John Wiley & Sons.

Bergan, P. G.; Horrigmoe, G.; Krekeland, B.; Søreide, H. (1978): Solution techniques for non-linear finite element problems. International Journal for Numerical Methods in Engineering, vol. 12, pp. 1677-1696.

Cardoso, C. O. (2005): Methodology for analysis and project of high pressure/temperatu re (HPHT) pipelines by application of finite element method (in Portuguese) (DSc-Thesi s), Federal University of Rio de Janeiro.

Costa, A. M. (1984): An application of computational methods and rock mechanics princ iples in design and analysis of underground excavations intended for the underground mi ning (in Portuguese). DSc Thesis, Federal University of Rio de Janeiro.

Crisfield, M. A. (1981): A fast incremental/iterative solution procedure that handles “sna p-throug”. Computers & Structures, vol. 13, pp. 55-62.

Elgohary, T. A.; Dong, L.; Junkins, J. L.; Atluri, S. N. (2014): Solution of post-buckli ng & limit load problems, without inverting the tangent stiffness matrix & without using arc-length methods. Computer Modeling in Engineering & Sciences, vol. 98, pp. 543-563.

Geers, M. G. D. (1999): Enhanced solution control for physically and geometrically non-linear problems. Part I – The subplane control approach. International Journal for Nume rical Methods in Engineering, vol. 46, pp. 177-204.

Gustafsson, K.; Soderlind, G. (1997): Control strategies for the iterative solutions of nonline ar equations in ODE solvers. SIAM Journal on Scientific Computing, vol. 18, pp. 23-40.

Hardyniec, A.; Chraney, F. (2015): A new efficient method for determining the collaps e margin ratio using parallel computing. Computers & Structures, vol. 148, pp. 14-25.

Koohestani, K. (2013): A hybrid method for efficient solution of geometrically nonlinear structures. International Journal of Solids and Structures, vol. 50, pp. 21-29.

Labeas, G. N.; Belesis, S. D. (2011): Efficient analysis of large-scale structural problems with geometrical non-linearity. International Journal of Non-Linear Mechanics, vol. 46,pp. 1283-1292.

Lambe, T. W.; Whitman, R. V. (1979): Soil mechanics, SI version. John Wiley & Sons.

Lindgaard, E.; Lund, E. (2010): Nonlinear buckling optimization of composite structur es. Computer Methods in Applied Mechanics and Engineering, vol. 199, pp. 2319-2330.

Luenberger, D. G. (1989): Linear and nonlinear programming. Addison-Wesley.

Ortega, J. M.; Rheinboldt, W. C. (1970): Iterative solution of nonlinear equations in se veral variables. Academic press.

Riks, E. (1979): An incremental approach to the solution of snapping and buckling probl ems. International Journal of Solids and Structures, vol. 15, pp. 529-551.

Ritto-Corrêa, M.; Camotim, D. (2008): On the arc-length quadratic control methods: Es tablished, less known and new implementation procedures. Computers & Structures, vol.86, pp. 1353-1368.

Schweizerhof, K. H.; Wriggers, P. (1986): Consistent linearization for path following m ethods in nonlinear FE analysis. Computer Methods in Applied Mechanics and Engineeri ng, vol. 59, pp. 261-279.

Sheng D.; Nazem, M.; Carter, J. P. (2009): Some computational aspects for solving dee p penetration problems in geomechanics. Computational Mechanics, vol. 44, pp. 549-561.

Sheng, D.; Sloan, S. W.; Yu, H. S. (2000): Aspects of finite element implementation of critical state models. Computational Mechanics, vol. 26, pp. 185-196.

Sheng, D.; Sloan, S. W. (2003): Time stepping schemes for coupled displacement and po re pressure analysis. Computational Mechanics, vol. 31, pp. 122-134.

Souza Neto, E. A.; Peric, D.; Owen, D. R. J. (2008): Computational methods for plastic ity. John Wiley & Sons.

Stull, J. S.; Earls, C. J.; Aquino, W. (2008): A posteriori initial imperfection identificati on in shell buckling problems. Computer Methods in Applied Mechanics and Engineering,vol. 198, pp. 260-268.