动力学中临界问题的教学设计

陈光才

(江苏省南京市第二十九中学，江苏 南京 210036)

·教学研究·

动力学中临界问题的教学设计

陈光才

(江苏省南京市第二十九中学，江苏 南京 210036)

本节课是在认知理论指导下，结合高一学生认知特点设计而成.在牛顿第二定律应用的教学设计中，考虑到临界问题本身较为抽象，学生理解起来有一定难度，所以在问题情景的选择上，选择高一学生熟悉的、容易接受的简单情景.整节课师生互动流畅，达到了学生自主学习、高效学习的目的.

认知理论；牛顿第二定律；临界问题

1 设计思路

从本质来说，教学是学生在教师指导下认识客观世界，使自身得到发展的实践形式.临界问题在高中物理学习中属于难度较大的内容，需要较强的逻辑思维能力和想象能力.涉及的教学内容也比较多，比如牛顿运动定律、圆周运动、能量、电磁场等.在高一刚学完牛顿第二定律时，来讲临界问题，如何才能让学生较轻松地学习？在设计本节课时，笔者力图充分发挥学生的主观能动性，体现学生的主体地位.由于临界问题本身就很难，所以在选择知识的情景时就要考虑到学生的认知能力，从简单的情况着手，这样可以增强学生的自我效能感，使学生坚信自己能够成功.因此，选择简单的情景，对知识的学习由易到难，稳扎稳打，可以有效增强学生的自我效能感，提高学习效率.

笔者认为分步骤、分层次教学不失为一种较为有效的教学方法，所谓分步骤就是从易到难、步步为营.对于本课来说，可以分为以下四步来实施课堂教学：首先，对于临界问题的概念给学生一个直观的认识，要求学生在解决临界问题时，能有发现临界状态的意识，有分析临界条件的思路，有解出临界值的方法；第二，发现临界状态.给出几个含临界状态的例题，让学生去寻找，在寻找过程中再次认识临界现象的概念.经过几个例题的训练，能使大部分学生能迅速找到临界状态.第三，分析临界条件.临界状态找到了，那么要达到这样的临界状态需要满足什么样的条件？引导学生从力、加速度、速度等角度去思考分析，找到相关的等量、不等量关系.第四，解出临界值.由临界条件列出方程或方程组，联立方程求解临界值.

2 教学目标

2.1 知识与技能

(1) 知道临界问题的概念，会分析、求解临界问题.

(2) 能熟练找出问题中隐含的临界问题，能发现临界状态.

(3) 会应用牛顿第二定律分析临界问题的条件，掌握求解临界问题的基本方法.

2.2 过程与方法

(1) 通过对临界问题的实例分析，渗透理论联系实际的观点，提高学生分析和解决问题的能力．

(2) 帮助学生学会运用实例，总结、归纳相关问题的解题规律.

2.3 情感、态度与价值观

(1) 通过对几个实例的分析，使学生明确具体问题必须具体分析，理解物理与生活的联系，学会用合理、科学的方法解决问题.

(2) 培养学生主观能动性，争做课堂的主人.

3 教学过程

3.1 复习引入，认识临界问题

高中物理知识多而繁杂，前后知识点联系紧密，逻辑性强.在学生进行新知识学习的同时，也要引导学生如何对旧知识进行复习、归纳和分类.让学生通过回忆，理解知识点之间的横、纵向联系.学会根据具体实例通过抽象形成理论知识，并用实践检验之.

通过前面的学习，学生已经可以熟练地应用牛顿第二定律求解常见的动力学问题：根据运动求力和根据力求运动，在这两类问题中牛顿第二定律都起到了关键的作用.

问题1：牛顿第二定律的内容是什么?

生:物体加速度的大小跟作用力成正比，跟物体的质量成反比，加速度的方向跟作用力的方向相同.

师：我们知道物体所受合外力与物体的加速度是瞬时对应关系，对于物体在某个运动过程中的任一状态F和a都是时刻对应的.

当物体由一种状态变为另一种状态时，可能伴随着受力或者加速度的变化，可能存在一个过渡的转折点，这时物体所处的状态通常称为临界状态，与之相关的物理条件则称为临界条件.

如何发现物理过程中隐含着临界状态？怎样分析临界状态满足的物理条件？这是我们这节课要学习的主要内容.

在许多临界问题中，题干常用“恰好”“最大”“至少”“不脱离”等词语对临界状态给出了明确的暗示，审题时一定要抓住这些特定的词语，挖掘其内涵，找出临界条件.

有些问题中并不显含上述常见的“临界术语”，但审题时发现某个物理量在变化过程中会发生突变，比如力、加速度、速度等，则该物理量突变时物体所处的状态即为临界状态.

3.2 进入新课，寻找临界状态

本着充分体现学生学习主体地位的原则，教师在教学活动中要发挥相应的引导作用.对于临界状态的寻找主要由学生来完成，为了充分提高课堂效率，让学生的自我效能感发挥重要作用，模型的选取也应从易到难、层层推进.

师：临界状态是介于两种状态之间过渡的转折点，通常伴随着物体从静止变为运动、从运动变为静止，物体的某个物理量从无到有或从有到无.

下面给大家举几个例子，来说明物体的运动过程，请大家找出这个过程中的临界状态.

如图1所示，在粗糙的水平地面上放一个物体B，在B上施加一个水平向右的力F，已知F从零开始逐渐变大，我们发现物体B前一段时间始终静止，后来运动起来，而且运动得越来越快.

图1

问题2:这个过程中存在临界状态吗?如果存在，是哪个状态?

生:有，是刚刚运动的那个状态.

师：很好，大家发现物体由静止变为运动了，而临界状态恰好是静止过程的终止状态，同时又是运动过程的开始状态，是从静止过渡到运动的一个转折点.

如图2所示，在粗糙的水平地面上放一个物体B，在B上放另一物体A，A与B之间有摩擦.在B上施加一个水平向右的力F，已知力F从零开始逐渐变大，我们发现物体B和A在前一段时间始终静止，后来一起运动起来，而且运动得越来越快.再后来发现A运动得没有B快了，他们之间发生了相对滑动.

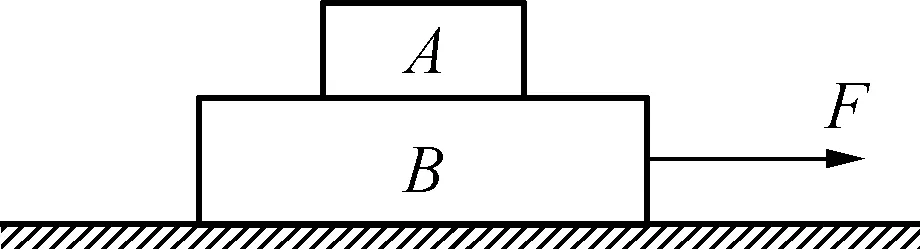
图2

问题3:请同学来找找这个过程的临界状态.

生1:在B刚相对地面运动的那个状态.

生2:在A刚相对于B运动的那个状态.

师：通过这两个例子的学习，大家应该知道如何寻找临界状态了，临界状态往往伴随着物体从静止变为运动或从运动变为静止.如图3所示，请大家来说说这个过程可能存在的临界状态.

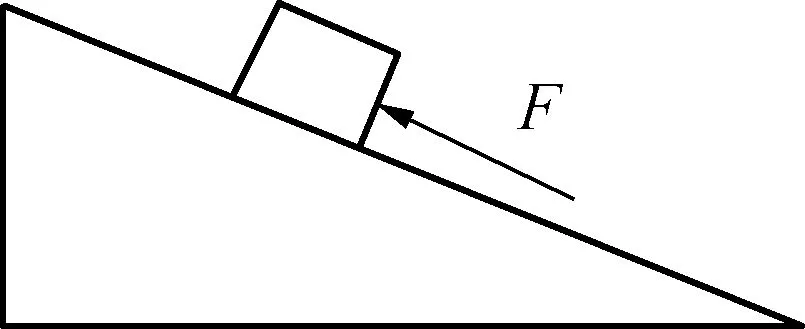
图3

生1:如果有F的时候物体是静止的，那么当F逐渐变小时，物体可能相对斜面下滑.在下滑的那个瞬间即为临界状态.

生2:如果F逐渐变大，物体可能相对斜面上滑.在上滑动那个瞬间即为临界状态.

师：大家说得很好，考虑得很全面.通过上面几个例子我们发现:可能隐含临界状态的特征是物体从静止变为运动(含相对运动)，当然如果物体从运动变为静止也往往隐含着临界状态.

如图4所示，当力F逐渐变大时，物体会被拖离地面，那么在离开地面的那个瞬间即为临界状态.

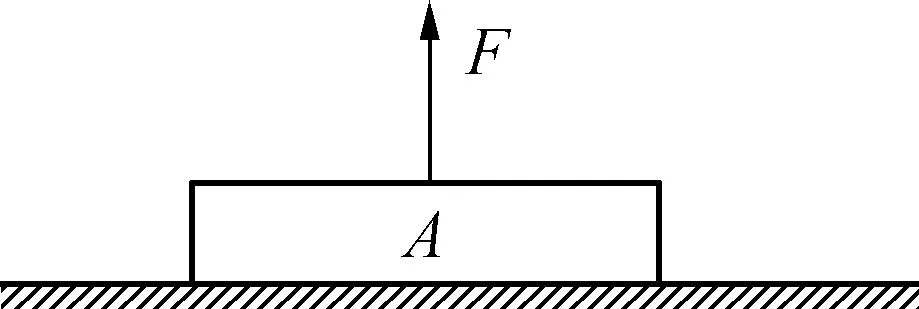
图4

如图5所示，当物体质量逐渐变大时，绳子会突然断裂，那么在断裂的那个瞬间即为临界状态.

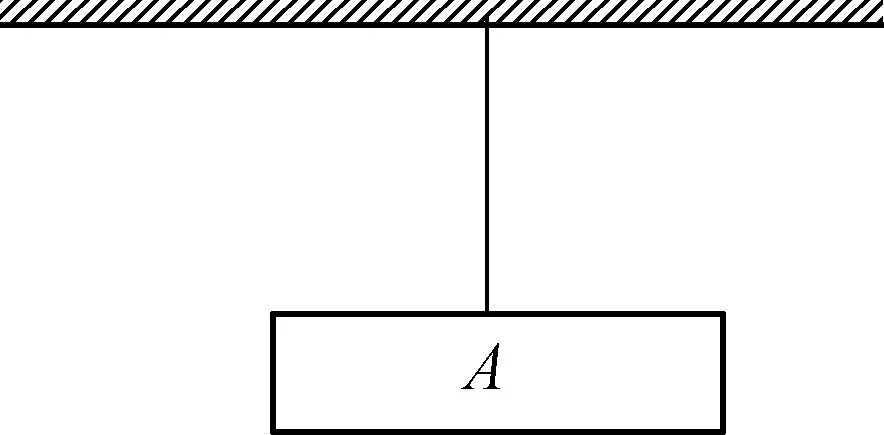
图5

如图6所示，斜面向右加速运动的加速度大到一定值后，小球会脱离斜面“飞”起来.刚“飞”的那个瞬间即为临界状态.

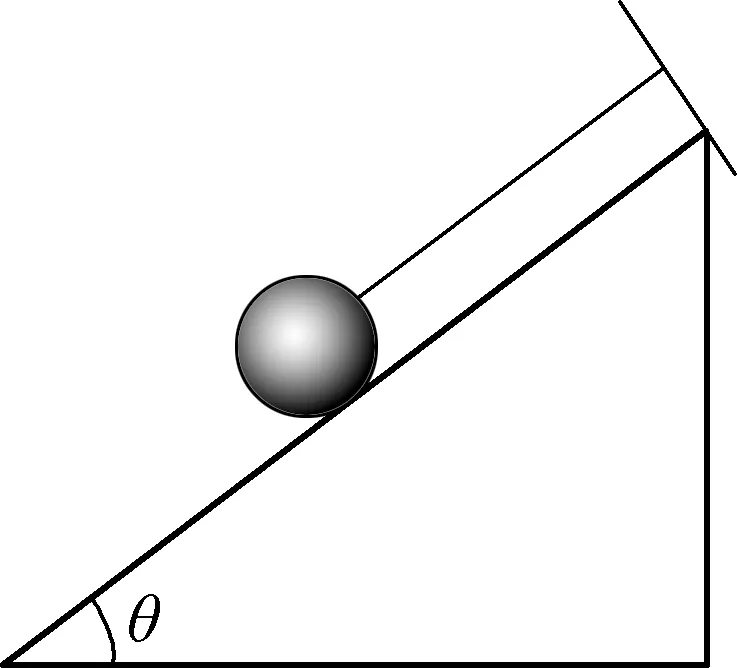
图6

通过这几个例子我们发现:可能隐含临界状态的特征是物体间发生分离.

1.3 渐入佳境，分析临界条件

高中生注意的集中性和稳定性有了很好的发展，有意注意已占主要地位，能够有意识地调控自己的注意，使之指向和集中于需要学习的事物中.在学生寻找临界状态的环节，已经获得十足的成就感，正信心百倍、迫不及待地希望解决新问题.在这种情况下分析临界条件，学生会积极参与，把课堂气氛推向高潮.

解答临界问题的关键是找临界条件，临界问题常常有这样几类临界条件：

(1) 存在静摩擦的连接系统，相对静止与相对滑动的临界条件是静摩擦力达最大值，即f=fm.

(2) 绳子断裂的临界条件是绳中张力达到最大值，即T=Tmax.

(3) 相互接触的两物体脱离的临界条件是相互作用的弹力为零，即FN=0.

在图1所示情景中，临界条件为B与地面间的摩擦力达到最大静摩擦力.

在图2所示情景中，临界条件为B与地面间的摩擦力达到最大静摩擦.另一个临界状态满足的条件是A与B之间的摩擦力达到最大静摩擦力.

在图3所示情景中，临界条件为物体与斜面间的摩擦力达到最大静摩擦力.

在图4所示情景中，临界条件为地面对A的支持力为零.

在图5所示情景中，临界条件为绳子对A的拉力达到绳子所能承受的最大拉力.

在图6所示情景中，临界条件为斜面对小球的支持力为零.

3.4 及时巩固，演练临界问题

高中生的思维具有更高的抽象概括性、反省性和监控性，他们一般能摆脱具体事物的限制，运用概念、提出假设、检验假设来进行抽象思维；能够用理论做指导，综合分析各种材料，不断加深对事物发展规律的认识，抽象逻辑思维趋向理论型.此时，进行适当的强化，以达到熟能生巧、触类旁通、举一反三的效果.

例1:如图2所示，物体A放在物体B上，物体B放在光滑的水平面上，已知mA=2kg，mB=6kg，A、B间最大静摩擦力为8N，则当F=16N拉B时，求A、B的加速度各为多少?

例2:如图6所示，一质量为0.2kg的小球静止在光滑的倾角为53°的斜面上，斜面静止时，小球紧靠在斜面上，细绳与斜面平行，当斜面以10m/s2加速度水平向右作匀加速直线运动时，求细绳对小球的拉力和斜面对小球的弹力.

4 教学反思

应用牛顿定律解决动力学问题的过程中，当物体运动加速度不同时，物体有可能处于不同的状态，特别是题目中出现“最大”“至少”“刚好”等词语时，往往伴随临界现象.临界问题通常具有一定的隐蔽性，解题灵活性较大，审题时应力求准确把握题目的物理情景，抓住临界状态的特征，找到正确的解题方向.

对于高一学生，临界问题显得有点抽象，所以在设计本课时，着眼点在如何才能让学生轻松接受，不至于产生畏难情绪.知识载体很重要，本文所选择的案例都是学生所熟知而且比较简单的物理模型，这样学生可以把注意力放到分析临界问题上.文中所选示例从易到难安排，教学时可以根据学生实际情况略作调整，对于基础一般的班级可以考虑删掉较难的例子，可以花工夫把简单的例子分析透彻，这样效果会更好.

[1] 周玉玲.高中生物新课改如何适应了高中生认知特点[J].北方文学，2010，(11).

[2] 吴建.高中生的心理转型及有效引导[J].教育科学论坛，2008，(6).