基于主断面参数的车身结构刚度链快速求解

刘子建+饶俊威+刘瑜+秦欢

摘 要：在刚度链计算模型中直接利用真实主断面参数快速求解，是车身结构刚度链设计方法必须解决的关键问题.在建立和完善轿车车身弯曲静刚度链计算模型的基础上，以刚度链节点参数可控和工程化为目标，建立了刚度链节点参数与主断面截面属性参数的对应关系，研究了利用极坐标法控制真实主断面形状的参数化方法，以及由单一变量控制的复杂截面属性计算方法，实现了刚度链节点属性的参数化计算和刚度链模型计算参数的工程化，为基于真实主断面结构形状的车身静刚度优化分配研究打下了基础.最后用一个车身轻量化优化计算实例验证了研究方法的可行性.

关键词：车身结构静刚度链；主断面；参数化；刚度优化分配

中图分类号：U463.82 文献标志码：A

Fast Calculation for Stiffness Chain of Vehicle-body

Structure Based on Parameters of Main Section

LIU Zijian，RAO Junwei，LIU Yu，QIN Huan

（State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body， Hunan University， Changsha 410082， China）

Abstract：The fast calculation of stiffness chain model by directly using the parameters of real main section is the key problem which should be solved in the design of vehicle-body stiffness chain. Taking the control and engineering on the parameters of stiffness chain nodes as the target， this paper evaluated the relationship between the parameters of stiffness chain nodes and the parameters of main section property. Furthermore， the parameterized method of controlling the real shape of the main section was studied by using the polar coordinate method and computing method of complex section properties that considers single variable control theory based on an established and improved computing model for static stiffness chain of vehicle body. It achieves the targets of parameterized calculation for the stiffness chain nodes and the engineering for the parameters in stiffness chain model， which provides a foundation for the investigation on the optimal distribution of static stiffness based on real main section structure and shape. Finally， the proposed method was verified by a numerical example of a light-weight of vehicle body.

Key words：static stiffness chain of vehicle-body structure； main section； parameterization； stiffness optimum distribution

汽车正向开发流程的车身工程设计阶段分为概念设计和详细设计.概念设计是车身结构设计的前期阶段，任务是为详细设计提供结构可行的方案.车身的整体结构及性能都取决于概念设计的结果，一旦留下设计缺陷，在后续流程中将难以弥补.现代轿车的车身一般采用承载式结构，车身需抵御汽车行驶的复杂载荷，因此，车身的刚度性能尤为重要.车身主断面是分布在车身各个重要位置，用以描述车身结构细节的横截面，它既是控制车身结构和性能的关键点，也是描述车身结构概念设计方案的重要工具.车身主断面的形状及尺寸是影响车身刚度性能的重要因素，因此，主断面设计是车身结构概念设计的重要内容.国内外学术界和工业界对汽车车身结构概念设计方法和车身刚度性能的研究高度重视.如本田汽车公司的Fujii等人[1]研究了基于拓扑优化技术的车身概念设计方法；福特汽车公司的工程师研究了一种基于重要零部件刚度性能的车身框架结构，建立了车身概念模型，并详细与有限元模型的静刚度和动刚度进行了分析对比，评估了概念设计模型的可靠性[2-3]；常伟波等人[4]提出了正面碰撞性能主导的轿车车身正向概念設计流程和方法；侯文彬等人[5]针对客车车身概念设计的特点，开发了客车车身结构概念设计与优化系统，等等.上述研究针对车身结构概念设计的某些具体问题提出了解决方法，然而，关于主断面优化与性能主导的正向概念设计方法关系的讨论还不多见.

本文在建立和完善轿车车身刚度链计算模型的基础上，以刚度链节点参数可控和工程化为目标，建立了节点参数与主断面截面属性参数的对应关系，研究了截面形状控制的参数化方法和对应的截面属性计算方法，提出了基于真实主断面结构形状的白车身刚度优化分配方法.论文最后以一个车身轻量化优化计算的实例，验证了以静刚度性能为主导的车身结构正向概念设计刚度链方法的可行性.

1 车身刚度链建模

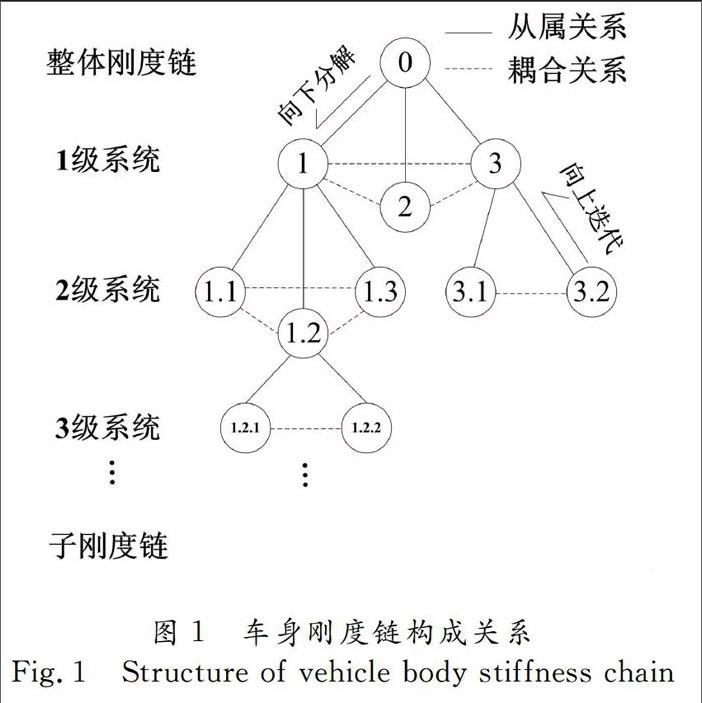
由车身的结构形式、材料特性、动静载荷所决定的车身整体刚度及其各部分刚度的作用关系，称为车身结构刚度链[6].车身刚度链以主断面、接头等为节点沿载荷传递路径分布，准确描述结构与材料、载荷与变形，以及节点之间的相互关系.依据刚度链概念，可以将车身结构分解成为多个子系统，每个子系统对应于一个子刚度链，形成树状层次结构的完整车身刚度链，如图1所示.如轿车车身总体上可分为横梁系统、左侧围系统、右侧围系统和底板系统等.依据构成关系和设计要求，以两前车轮轴中心点为原点，X轴水平向后，Z轴垂直向上建立整车设计坐标系S0.进一步建立梁单元表示的车身结构简化几何模型，确定主断面的数量和位置，按照构成关系对节点编号，获得某车型1/2车身的具有18个主断面的车身刚度链几何模型如图2所示.利用对称性，不难得到整个车身的刚度链几何模型.

以如图3所示的车身弯曲工况[7]为例，讨论图2所示刚度链的静刚度分析模型.按照车身刚度测试规范，在车身后悬架位置处约束X，Y，Z方向的平动自由度，前悬架位置处约束Y，Z方向的平动自由度，在座椅安装点左右对称施加垂直向下的力F=1 000 N，车身整体的弯曲刚度由车身底架处最大垂直挠度来评价.

首先讨论车身侧围刚度链分析模型.左侧围的受力及单元划分情况如图4所示，其中0，1，2，…，15为多个梁单元相交的节点；①，②，…，B17为主断面所在处的梁单元；共有16个节点和17个单元，添加约束和外载荷如图4所示.

侧围刚度链的组成单元及其所对应的主断面编号如表1所示.依据表1中主断面与单元的对应关系，设与某一主断面对应的组成单元具有相同的截面属性，可以将17个单元的横截面特性用9个截面属性集合来描述，即主断面属性，记为C（i）={A Iy Iz}（i），其中i为主断面编号，取值分别为1，4，5，8，9，10，12，13和15，与图2中主断面编号一致；A为主断面面积；Iy，Iz为主断面惯性矩.

以图5（a）所示的子刚度链1为例讨论刚度链计算模型.子刚度链1主要是由前纵梁、门槛梁以及后地板纵梁组合而成，为了真实地模拟刚度链1的受力情况，在节点0和节点7处添加铰链约束，将整体视为一个简支连续梁结构，且各个组成单元可以具有不同的截面属性.在节点2处添加竖直向下的集中载荷F，在耦合点1，3，6处添加未知状态向量，故可以推导出节点0和节点7的状态向量，以及节点1-6的载荷向量.

对连续梁结构求解状态向量时，可以利用传递矩阵法[8-9]建立数学模型.子刚度链1所对应的连续梁结构，可以离散成7个单元，单元编号依次为①，②，…，⑦，其中单元①的抗拉刚度、抗弯刚度、抗剪切刚度分别为EA（1），EI（1） ，GA（1）/μ（下标为单元对应的主断面编号，下同）；单元②，③，④的抗拉刚度、抗弯刚度、抗剪切刚度分别为EA（10），EI（10） ，GA（10）/μ；单元⑤，⑥，⑦的抗拉刚度、抗弯刚度、抗剪切刚度分别为EA（12），EI（12） ，GA（12）/μ；单元长度依次为l（1），l（2），…，l（7）.如图6所示.

根据传递矩阵法可求出最右端状态向量Sr（7）和最左端状态向量Sl（1）的递推关系如下：

Sr7=T7Sl7

Sl7=F6Sr6

Sr6=T6Sl6

Sl6=F5Sr5

Sr2=T2Sl2

Sl2=F1Sr1

Sr1=T1Sl1 （1）

式中：T（i）为单元i的场矩阵；F（i）为节点i的载荷向量.如：节点0处为铰接约束，只有径向约束剪力Ql以及平面内的转角φl，节点0的状态向量为Sl（1）={0，Ql，0，0，0，φl}T（1） ；在节点2处只承受有垂直向下集中载荷F，节点2处的载荷向量为F2={0，F，0，0，0，0}T（2），等等.

将方程组（1）从下往上迭代，可确定最右端节点状态向量Sr（7）和最左端节点状态向量Sl（1）的关系式，即传递方程：

Sr7=[∏6i=1（T8-i×F7-i）]×

T1×Sl1（2）

除单元⑤和单元⑥之外，其他单元的局部坐标系均与整车设计坐标系S0平行，它们的场矩阵T（i）表达式为：

Ti=

1000000100000li1000-liEAi001000-l3i6EIi-μliGAil2i2EIi01li0-l2i2EIi-liEIi001 i≠5，6 （3）

單元⑤和⑥的局部坐标系与整车设计坐标系S0之间存在一个夹角，通过坐标变换有：

Tk=λ-1kkλk（4）

式中：T（k）为单元k在S0坐标系中的场矩阵；（k）为单元k在局部坐标系Sk中的场矩阵.

对图5中的子刚度链2和子刚度链3也可以进行类似的讨论.

设节点2处在集中载荷F作用下竖直向下变形量Δz为基本未知量，利用静平衡条件和传递方程（2）可以求得子刚度链1的弯曲变形量Δz与各主断面截面属性集合C（i）的关系表达式：

f1C1，C10，C12，Δz=0（5）

子刚度链1与子刚度链2在节点1和节点6处耦合，建立两者的耦合方程：

Sl（2）-Sl（8）=0

Sl（7）-Sl（15）=0 （6）

同理，可得出子刚度链2和子刚度链3的数学模型及子刚度链间的耦合方程.将上述3个子刚度链数学模型简单记为f1，f2和f3，耦合方程分别记为Q1（2），Q1（3）和Q2（3）.

由上述讨论可得如下方程：

f1=0

f2=0

f3=0

Q1（2）=0

Q1（3）=0

Q2（3）=0（7）

方程组（7）即为车身左侧围的静态刚度链数学模型，记为F1，同理可得车身右侧围和9个横梁的刚度链模型，分别记为F2，F3，F4，…，F11.子系统刚度链i与子系统刚度链j的耦合方程记为Gi（j），则车身整体刚度链模型为：

F1，F2，…，F11T=0

G1（3），G1（4），…，G1（11），G2（3），

G2（4），…，G2（11）T=0 （8）

根据方程组（8）可以求得节点2竖直向下的变形量Δz与各主断面属性C（i）之间的函数关系式：

Δz=f（C1，C2，…，C18）（9）

式中：变形量Δz由18个主断面的截面属性集合（即54个变量）表示，如果直接对这些参数进行优化，将会遇到优化变量太多且优化出来的数据无法对主断面具体形状进行描述等问题.因此，有必要对主断面形状参数化和截面属性计算方法进行研究.

2 主断面属性计算及形状参数化方法

车身主断面是由若干钣金件焊接而成的形状复杂的封闭截面，图7（a）所示为某车门槛梁主断面实物图.由于主断面的形状、面积、惯性矩等截面属性是决定车身刚度、强度、加工工艺性等的关键因素，因此，准确求取各种形状主断面的截面属性，并根据车身性能设计要求优化匹配多个主断面的属性参数，是实现车身优化设计必须解决的关键问题.现有的处理方法是将主断面简化成为矩形或圆形等简单形状进行计算[10]，求解结果与实际情况差距较大.由式（8）所示刚度链计算模型和车身弯曲变形计算公式（9）可知，只要建立车身实际主断面形状属性参数的计算方法，就可以利用刚度链方法对实际车身结构进行分析优化，大幅提高设计质量，具有重要意义.

2.1 主断面属性参数计算

基于真实主断面形状的截面参数计算仍需要进行少量简化，简化原则如下：

1） 忽略加工工艺要求的小结构，如小圆角、小倒角等，将其简化为一个点；

2） 曲率不大的曲线段，在尊重原断面形状的前提下，用直线代替.

如图7（b）所示为简化后的门槛梁主断面形状，它是由多条直线段经结点连接而成的封闭图形.

设主断面由n条直线连接构成，将其分成n个区段.设第i个区段的长度为Li，板厚为ti，如图8所示（图中数字表示结点编号），则由弗拉索夫薄壁杆件理论[11]可推导出用分段法求取主断面实体部分面积和惯性矩的计算公式如式（10），（11）和（12）所示.

2.2 主断面形状参数化方法

车身主断面由外板、内板和加强板组成.主断面形状不仅取决于刚度、强度、工艺、碰撞安全等车身性能的需求，而且与整车外观造型、总布置和内饰设计密切相关，在车身结构设计中经常变化.针对2.1节讨论的主断面属性参数计算公式，进一步研究一种简单有效的主断面形状参数化生成方法，是利用刚度链模型进行车身刚度优化设计必不可少的重要环节.

文献[12]提出了一种基于极坐标的截面形状计算公式如式（13）所示.

r′i=（π-dv-δik×π+1）ri （13）

式中：（ri，δi）（δi的单位为弧度）为截面实体部分上点的极坐标；k为形状变化程度控制系数，通常可取k=2；dv（dv∈（0，2π））为极坐标控制参数.下面讨论利用式（13）实现主断面形状控制的方法.设已知图8所示主断面，以截面参考坐标系原点o为极点，z轴正方向为极轴，建立极坐标系，如图9所示，则可计算出该主断面所有结点的极坐标值（ri，δi）.在此基础上，对应于一个给定的dv值，由式（13）计算出一组新结点的极坐标值（r′i，δi），依次连接这些新结点，即可获得与原截面形状类似的新截面.当dv-δi>π时，计算点的极径ri将减小，反之将增大，从而对截面形状进行连续的控制，极径ri的变化程度取决于dv和k的取值.

利用式（13）控制图8所示主断面形状时须特别注意外板的处理.图8中结点1至结点8表示的车身外板部分的形状是车身设计流程已经冻结的A级面确定的，不允许进行修改，故形状参数化设计的主要对象是内板和加强板.另外，在确定参数化结点和参数变化区间时还需考虑冲压工艺和装配要求等因素，如防止出现冲压负角等.图9为针对结点9，10，14，15，16，17应用式（13）控制门槛梁主断面形状变化的情况，此时dv的取值为1.5，k的取值为2.

2.3 dv控制的主断面属性计算

下面继续以门槛梁为例介绍基于形状控制参数dv的主断面属性计算步骤.

第一步是將门槛梁原始主断面的结点坐标转换为极坐标.其二是确定k值，并给定一个dv值，代入式（13），逐个计算出变形后新主断面各结点的极坐标值.其三是将新结点的极坐标值换算成为oxyz坐标系下的直角坐标值.最后利用式（10），式（11）和式（12）计算新主断面属性值.表2为设计变量dv分别取1.1，1.2，1.3，1.4，1.5时计算所得门槛梁主断面属性值.

上述直接利用式（10）至式（12）计算截面属性的方法不仅步骤较多，需频繁地进行坐标换算，而且是逐点求解，计算效率难以提高.为了适应主断面优化设计中高效迭代求精计算的需求，依据表2数据拟合只有一个变量dv的门槛梁主断面属性近似计算公式：

A=106.4×dv+289.7 （14）

Iyy=62 640×dv2+ 87 800×dv+82 140 （15）

Izz=11 900×dv2-7 236×dv+13 680 （16）

同理，利用上述方法可以拟合出其他主断面属性关于形状控制参数dv的函数关系，在此不再一一赘述.

可以通过对比分析验证所拟合公式的准确性.如将公式（11）计算出来的Iyy精确值与公式（15）计算出来的Iyy拟合值进行对比，分析结果如表3所示.

结果表明拟合计算的最大的误差为3%.同样可以对A和Izz进行类似的计算误差分析，可以认为拟合公式具有较好的计算精度.调整和优化dv的取值方式还可以进一步减少计算误差.

上述方法可将车身的某一主断面形状由一个参数dv来控制，并且主断面的所有截面属性均是关于dv的函数，因此在进行主断面属性参数优化匹配时，每个主断面只需对一个参数进行优化，在大大减少优化计算难度，提高优化效率的同时，可以直接获得与工程设计要求吻合度很高的主断面，从而为车身设计精度提供保障.

3 主断面驱动的车身刚度优化分配

下面将主断面形状和截面属性的参数化设计方法与车身刚度链计算模型相结合，进一步研究基于刚度链方法的车身结构优化设计问题，目的是实现主断面属性驱动的车身刚度优化分配.讨论弯曲工况下车身主断面的优化问题.选取的设计变量为18个主断面属性参数：

X=[X1，X2，…，X18]T（17）

式中：

Xi={dv（i），t（i）}T （18）

式中：dv（i）（dv（i）∈（0，2π））和t（i）为第i个主断面的截面属性参数，dv（i）的初值设为1.为了减少计算量，取相同板厚t（i）=0.8 mm，所以需要进行优化的设计变量共有18个.

考虑车身的弯曲工况和设计要求，在节点2处添加竖直向下的载荷F=1 000 N，约束条件为加载处竖直向下位移Δz≤1 mm，由式（9）有：

Δz=f（C1，C2，…，C18）≤1 mm （19）

车身的整体刚度表达式为：

k弯=2F/Δz （20）

在满足车身弯曲刚度的条件下须使车身的质量最小，因此建立车身轻量化设计的目标函数为：

min f（m）=ρ∑18i=1（A（i）l（i）） （21）

式中：A（i）为第i根梁的截面面积，其值是关于dv（i）的函数；ρ为已知的材料密度；l（i）为第i根梁的结构长度，其值可以通过车身简化几何模型（图2）得到.

由上述设计变量、目标函数和约束条件决定的优化计算模型得：

X=[X1，X2，…，X18]T

min f（m）=ρ∑18i=1（A（i）l（i））

s.t. 0≤Δz≤1 mm （22）

求解式（22）时，首先根据产品研发要求和设计经验确定一组原始主断面，编写刚度链计算和各主断面属性拟合的MATLAB程序，并调用适当的优化计算模块完成优化计算.表4是采用遗传算法[13]，经过160步迭代使目标函数收敛后求得的车身侧围主断面形状控制参数dv的优化结果（其他主断面的优化结果不再一一列出），此时，在满足弯曲刚度约束条件下，白车身的最轻质量为0.212 5 T，弯曲刚度为3 260 N/mm.

根据得到的dv优化值进一步计算各主断面的结点坐标，利用拟合公式计算优化后截面属性，如表5所示.图10为门槛梁主断面形状优化前后的对比图，其中实线为优化前的主断面形状，虚线为优化后形状的变化部分.

为了验证刚度链设计方法的可行性，本文利用車身详细有限元模型，加载弯曲工况后模型如图11所示，该模型包括461 942个单元、465 722个节点、17 925个焊点.将上述模型用刚度链方法优化所得主断面形状赋予有限元模型的相应部位，进行计算，并对两个模型计算所得的弯曲刚度和车身质量大小进行对比分析，结果如表6所示.

根据表6数据可得到刚度链设计方法计算出的弯曲刚度与修改后有限元模型计算出的弯曲刚度误差仅为1.3%，表明刚度链方法与传统有限元方法的误差在合理的范围内，将刚度链方法优化出来的主断面形状赋予有限元模型，修改后的有限元模型的弯曲刚度（3 218 N/mm）明显高于初始有限元模型（3 112 N/mm）且质量越轻（减少了1.4%）.

4 结 论

本文依据车身结构刚度链构成关系，在分别建立各子刚度链和耦合方程的基础上，采用传递矩阵法建立了车身静刚度链计算模型，并明确了刚度链节点参数与主断面截面属性参数的对应关系；以真实主断面形状为对象，利用极坐标法建立了形状参数化控制方法，以及由单一变量dv控制的截面属性计算方法，并验证了计算方法的准确性；本文的研究实现了刚度链节点属性的参数化计算和刚度链模型计算对象的工程化，为基于真实主断面结构形状的车身刚度优化分配研究打下了基础.最后以一个车身轻量化优化计算实例验证了研究方法的可行性和优越性.

本文仅对弯曲工况下主断面进行了优化.如何结合刚度链方法综合考虑车身NVH、安全、工艺等多学科因素，完成车身所有主断面的优化设计，是值得深入研究的问题.

参考文献

[1] FUJII T，SHIBUYA S，SATO Y，et al.New body in white concept through topology optimisation[J].VDI-Berichte，2004，1846：603-616.

[2] PRATER G， SHAHHOSSEINI A M， KUO E Y， et al. Finite element concept models for vehicle architecture assessment and optimization[R]. Washington DC：SAE International，2005.

[3] TORSTENFELT B，KLARBRING A.Conceptual optimal design of modular car product families using simultaneous size， shape and topology optimization[J]. Finite Elements in Analysis and Design，2007，43（14）：1050-1061.

[4] 常伟波，张维刚，崔杰，等. 基于正面碰撞的轿车车身正向概念设计的研究[J]. 汽车工程，2012，34（5）：447-451.

CHANG Weibo， ZHANG Weigang， CUI Jie， et al. A research on the forward concept design of car body for frontal crash[J]. Automotive Engineering，2012，34（5）： 447-451.（In Chinese）

[5] 侯文彬，张红哲，徐金亭，等. 基于概念设计的客车车身结构设计与优化系统[J]. 湖南大学学报：自然科学版， 2013，40（10）：58-63.

HOU Wenbin，ZHANG Hongzhe，XU Jingting，et al. System of design and optimization system for bus body structure based on concept design[J].Journal of Hunan University： Natural Sciences， 2013，40（10）：58-63. （In Chinese）

[6] 田海豹. 基于剛度链方法的车身概念设计研究[D]. 长沙：湖南大学机械与运载工程学院， 2013.

TIAN Haibao. Study on conceptual design of car body using stiffness chain[D].Changsha：College of Mechanical and Vehicle Engineering， Hunan University，2013. （In Chinese）

[7] 季枫，王登峰，陈书明，等. 轿车白车身隐式全参数化建模与多目标轻量化优化[J]. 汽车工程，2014，36（2）：254-258.

JI Feng， WANG Dengfeng， CHEN Shuming， et al. Implicit parameterization modeling and multiobjective lightweight optimization for a cars body in white[J].Automotive Engineering，2014，36（2）：254-258. （In Chinese）

[8] 刘庆潭，倪国荣. 结构分析中的传递矩阵法[M].北京：中国铁道出版社，1997：1-12.

LIU Qingtan，NI Guorong.The transfer matrix method in structure analysis[M].Beijing：China Railway Publishing House，1997：1-12. （In Chinese）

[9] 闫仙丽，李青宁. 曲线箱梁桥的空间传递矩阵[J]. 哈尔滨工程大学学报，2014，35（10）：1-5.

YAN Xianli， LI Qingning.The spatial transfer matrix of curved box-girder bridge[J]. Journal of Harbin Engineering University，2014，35（10）：1-5. （In Chinese）

[10]刘子建，周小龙，田海豹，等. 基于主断面刚度优化分配的车身正向概念设计[J]. 中国机械工程，2015，26（6）：837-843.

LIU Zijian，ZHOU Xiaolong，TIAN Haibao，et al.Forward concept design of car body using stiffness optimal allocation of main sections[J].China Mechanical Engineering，2015，26（6）：837-843.（In Chinese）

[11]MURRAY N W. Introduction to the theory of thinwalled structure[M].Oxford：Oxford University Press，1984：120-124.

[12]蔡世民. 概念车身智能化CAE分析—1D梁截面优化研究[D].长春：吉林大学汽车工程学院，2007.

CAI Shiming.Concept auto body intellectualized CAE analysis—research of 1D beam section's optimization[D].Changchun：College of Automotive Engineering， Jilin University，2007.（In Chinese）

[13]玄光男，程润伟.遗传算法与工程优化[M].北京：清华大学出版社，2009：21-30.

XUAN Guangnan，CHENG Runwei.Genetic algorithms and engineering optimization[M].Beijing：Tsinghua University Press，2009：21-30.（In Chinese）