考虑励磁调节作用及发电机饱和的静态稳定性

郭 帅，康锦萍，许国瑞，张志坚

(1.华北电力大学 电气与电子工程学院，北京 102206；2．国网北京电力公司，北京 100031)

考虑励磁调节作用及发电机饱和的静态稳定性

郭 帅1，康锦萍1，许国瑞1，张志坚2

(1.华北电力大学 电气与电子工程学院，北京 102206；2．国网北京电力公司，北京 100031)

为了研究发电机饱和及励磁调节共同作用时对其静态稳定性的影响,提出了计及励磁调节器作用的功角曲线有限元算法，对比分析了发电机饱和及励磁调节作用对发电机极限功率和极限功角的影响。将用该方法计算的功角曲线用于小扰动后励磁调节器放大倍数的极限值和发电机运行极限的确定。结果表明，励磁调节器作用时发电机的静稳极限要增大，但若同时考虑同步发电机饱和作用，静稳极限要有所减小；发电机受到小扰动后，考虑同步发电机饱和作用时励磁调节器的放大倍数范围明显减小，发电机励磁电流调节量增大。研究结果为励磁调节器的参数整定与系统动态仿真提供必要的理论基础。

汽轮发电机；磁场饱和；有限元；功角曲线；静态稳定性

0 引 言

励磁调节器对于发电机的静态稳定性起着至关重要的作用，而同步电机饱和作用又影响着发电机的运行行为，因此需要研究同步电机饱和及励磁调节共同作用下的静态稳定性。

传统的静态稳定分析以系统在某一确定运行 点处的线性化模型为基础，通过特征分析法对发电机的静态稳定性进行计算[1]。这种方法通常不考虑发电机运行点处磁场饱和作用的影响。在发电机运行过程中，磁场饱和作用比较复杂。已有研究表明发电机在运行时发电机内存在磁路饱和，磁场畸变，交叉磁化等多个非线性因素的共同作用[2-4]。因此为了更加准确的分析法发电机的静态稳定性，有必要对同步发电机饱和作用进行深入研究。

在传统的静态稳定分析理论中，以发电机功角特性曲线作为辅助方程以推导发电机线性化模型，考虑励磁调节作用后的发电机功角曲线常采用发电机暂态电势E′q及发电机端电压UG为恒定时的功角曲线,其中功角曲线一般采用解析法计算，不能有效地反映同步发电机饱和作用的影响。

为了研究同步发电机饱和与励磁调节共同作用对静态稳定性的影响，本文以发电机单机无穷大系统为例，提出了计及励磁调节器作用的功角曲线有限元算法，计算了保持发电机电势恒定、发电机暂态电势恒定及发电机机端电压恒定时的功角曲线；然后通过与解析法计算结果进行对比，研究了同步发电机饱和作用对静态稳定性的影响，并对小扰动后励磁电流的调节量进行了比较。最后根据发电机的静态稳定判据计算了励磁调节器放大倍数的最大极限值和发电机的运行极限，对比了解析法与时步有限元法计算结果的差异。研究结果为考虑发电机饱和作用下的静态稳定性分析提供必要的理论基础。

1 励磁调节作用下的功角曲线计算

本文以单机无穷大系统为例来计算励磁调节作用下的发电机功角曲线。系统模型如图1所示，其中xe为联系电抗，U为系统电压，UG为发电机机端电压。发电机的负载相量图如图2所示。

图1 发电机单机无穷大系统Fig.1 Model of one machine infinite-bus system

图2 负载时发电机相量图Fig.2 Vector diagram of loading generator

1.1 功角曲线的有限元计算方法

对于电力系统中稳定运行的发电机而言，其运行工况主要是由发电机的定子电压、定子电流和发电机功角(或功率因数)决定[5]。在有限元计算中常采用上述状态变量作为端点量进行迭代计算。文献[5]采用端电压和功角作为端点量进行迭代，计算了不考虑励磁调节作用的发电机功角特性曲线。由于励磁调节器的作用，发电机受到小扰动后的励磁电流不再是恒定值，采用端电压和功角作为端点量不能唯一确定发电机状态，从而无法进行迭代计算。本文针对此问题，提出了发电机3个端点量迭代的基于有限元法的功角特性计算方法。下面以保持发电机暂态电势恒定时的功角特性计算说明迭代过程。

1.2 3个端点量的迭代算法

在保持励磁电流If、相角λ不变的情况下，使电枢电流I有一个微增量ΔI并进行磁场非线性迭代得到新的端点量，利用数值差分的方法得到新端点量对I的变化率，记作

同样分别给定励磁电流If和相角λ一个微增量，进行磁场非线性迭代可以得到新的端点量对If、λ的变化率，分别记作

设ΔI、Δλ、ΔIf为修正量，将上面的系数带入公式(1)：

(1)

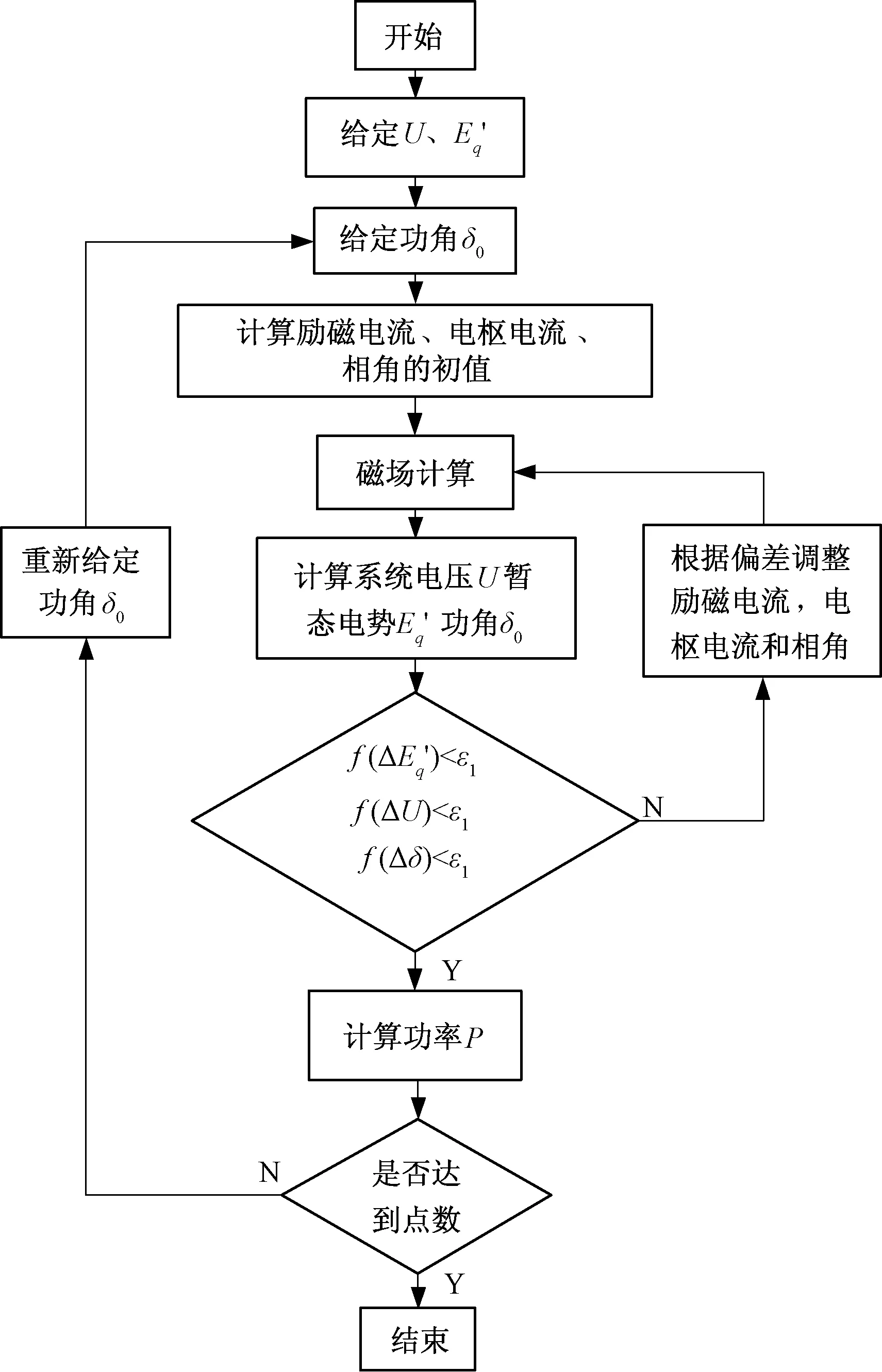
图3 功角特性计算流程图Fig.3 Flowchart of calculating power-angle curve

1.3 功角曲线的解析计算方法

以发电机空载电势Eq和电抗xd表示发电机，由图2可得

(2)

其中xdΣ=xd+xe， 将式(2)带入功率表达式

(3)

得到以发电机空载电势Eq表示的有功功率达式为

(4)

(5)

(6)

以发电机端电压UG和联系电抗xe表示发电机，可得此时的功角特性为

(7)

其中δG为UG与U之间的夹角。

(8)

1.4 基于功角曲线的发电机静态稳定判据

本文采用比例式调节器为例进行分析，发电机配置直流机励磁系统[1]，其简化传递函数如图4，放大系数为KA，本文不考虑励磁机时间常数的影响，设TE=0，得到励磁系统传递函数为

(9)

图4 励磁系统框图Fig.4 Diagram of excitation system

根据文献[1]对发电机实用模型方程和功率方程进行线性化处理得到了发电机动态方程如下：

(10)

其中

消去代数方程及非状态变量，求得发电机状态方程如下

(12)

根据发电机状态方程可以得到对应的特征方程。通过胡尔维茨判别法，即可获得保持系统稳定的条件[1]。进一步对稳定条件进行分析可以得到发电机静态稳定判据如式(13)所示:

式中：KAmax，KAmin分别为放大系数最大值和最小值。

为了充分考虑同步电机的饱和作用，发电机稳定判据中的系数应取饱和参数进行计算。根据定义系数SEq、REq、SE′q、RE′q、Sug、Rug由功角曲线分别对功角和对应电势求导得到。由于基于有限元法计算的功角曲线无法直接进行求导计算，本文采用差分法对功角曲线求取稳态运行点处的各系数。不计同步发电机饱和作用时的系数，通过功角曲线解析法公式直接求导得到。

2 同步发电机饱和及励磁调节共同作用下静态稳定极限

以300MW汽轮发电机为例，分别运用解析法和有限元法计算发电机功角特性曲线，其中解析法不考虑饱和作用，采用1.3节中的解析法公式计算，发电机电抗取不饱和值；有限元法计算考虑饱和作用1.1节中的方法。采用发电机参数见表1所示。

表1 300 MW汽轮发电机参数

2.1 发电机电势恒定的功角曲线

发电机额定励磁下，采用两种方法计算的有功功角特性如图5所示。

图5 发电机功角曲线Fig.5 Turbine generator power-angle curve

从图5中可以看出解析法和有限元法的计算结果很接近，发电机的极限功率和极限功角相差都很小，这是由于计及饱和与不计饱和时的发电机励磁功率近似相等。文献[5]中就发电机饱和作用对功角曲线的影响进行了详细分析。

表2给出了额定励磁电流下，不同系统电压时的发电机极限功角及极限功率的比较。从表2中可以看出同步发电机计及饱和后，发电机功率极限有所减小，在正常运行工况下，减小量不超过4.31%，在非正常工况下，系统电压变为1.2时，减小量不超过6%。可见发电机饱和对发电机的极限功率影响不大。

2.2 发电机暂态电势恒定的功角曲线

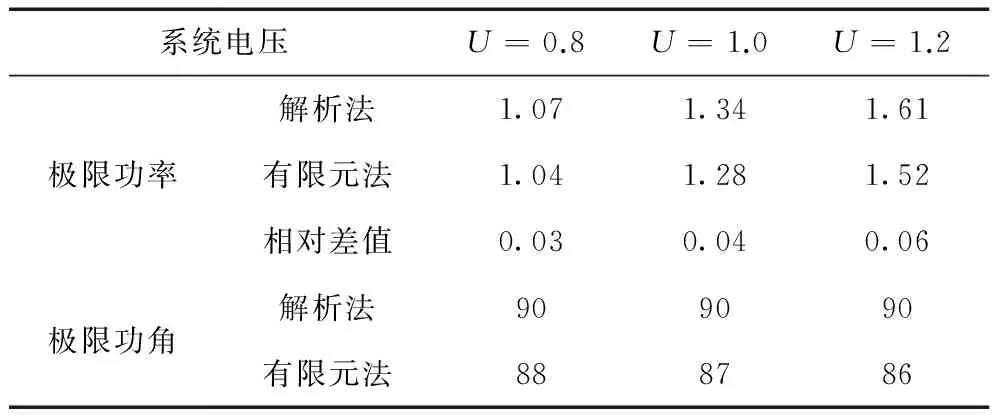
表2 额定励磁下的极限功率和极限功角

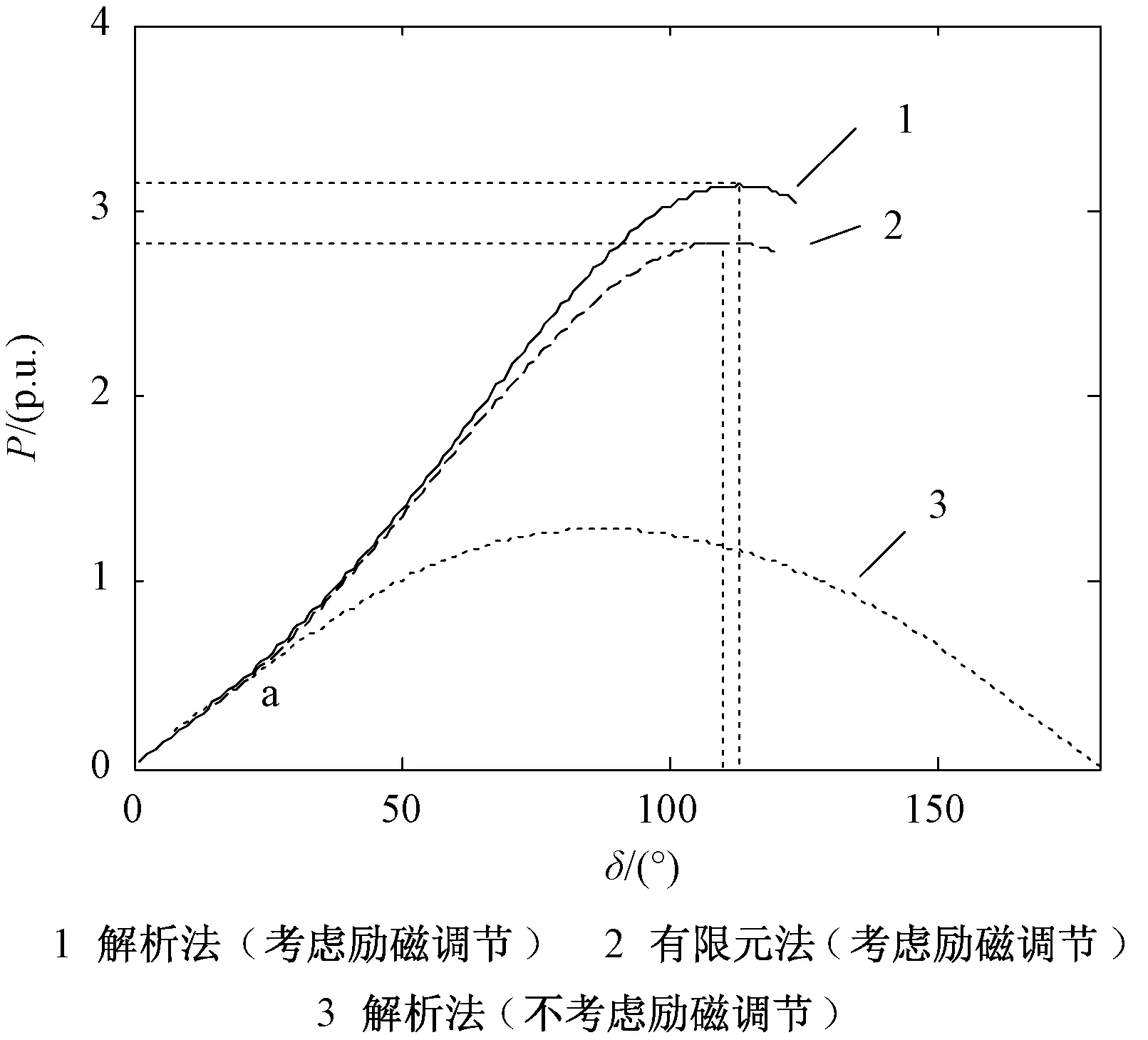
图=c的功角曲线Fig.6 Power-angle curves of =c

图6中的1、3曲线表明考虑励磁调节器作用的发电机静态稳定性明显增加。在励磁调节器的作用下，不计发电机饱和时，发电机的极限功率为3.13,极限功角为113°。文献[8]对某一300MW机组进行励磁系统控制实验，说明装设励磁调节器后发电机的极限功率出现在功角δ>90°处，进入人工稳定区，增大了静态稳定区域的范围。从1、2曲线中可以看出计及发电机饱和后极限功率变为2.82，减少了14%，极限功角变为110°。

2.3 发电机端电压恒定的功角曲线

仍以图5中的a点作为发电机的初始运行状态。发电机发生小扰动后，由于励磁调节器作用可保持发电机端电压恒定不变，运用1.1节中的有限元计算方法，对发电机端电压、发电机功角及系统电压进行迭代，计算机端电压保持恒定的功角曲线如图7所示。计算时发现利用有限元法计算时功角大于107°之后已经不再收敛。这主要是因为此时发电机功角较大，处于满载状态，励磁调节器的放大倍数太大，使得系统阻尼转矩系数小于零，系统产生了负阻尼转矩，从而引起了系统的振荡失稳。当发电机功角较小，发电机在轻负荷运行时，此时的系统阻尼转矩系数大于零，不会因为励磁调节器的投入而失步，功角特性可以收敛[9,10]。

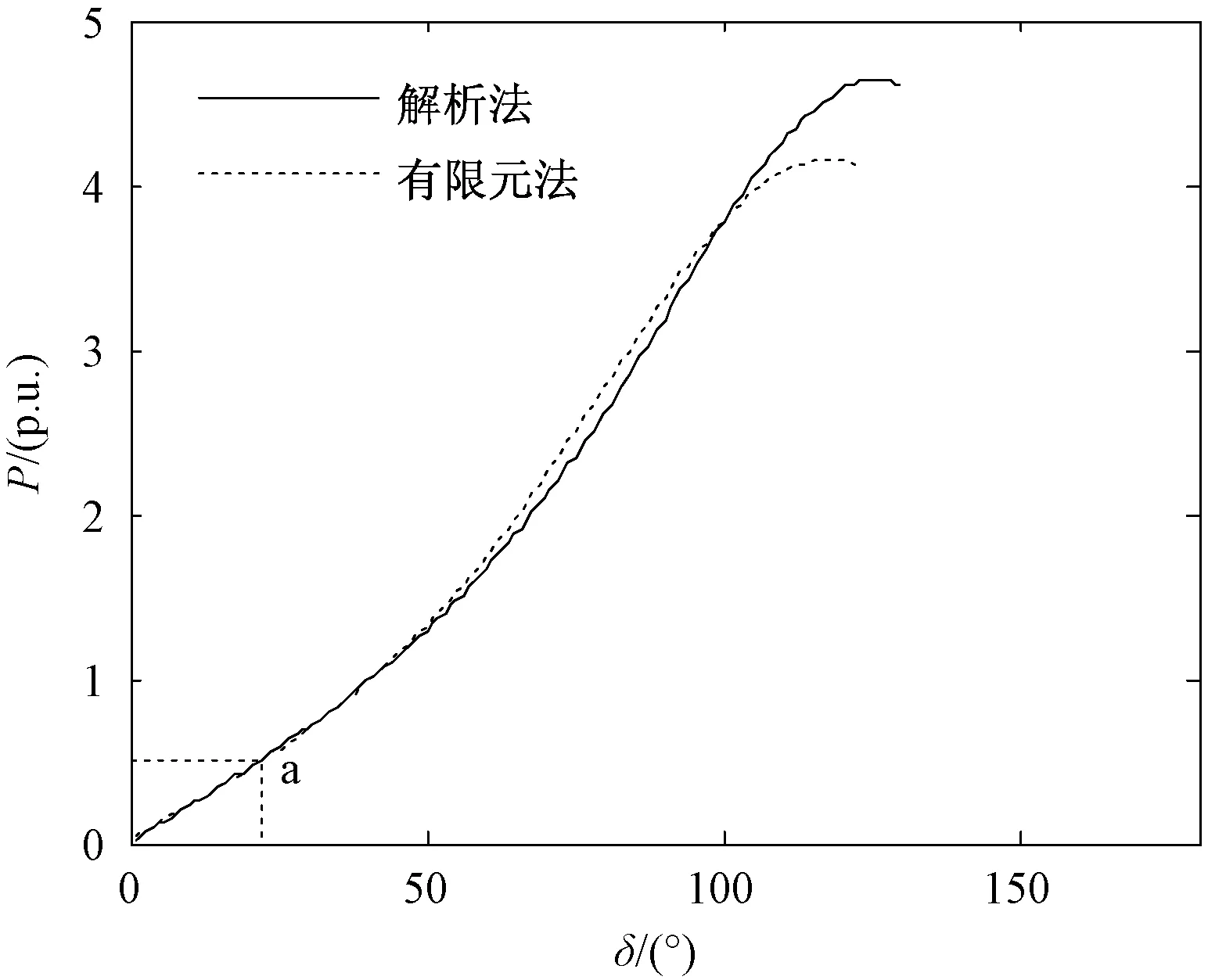
图7 UG=c的功角曲线Fig.7 Power-angle curve of UG=c

由图7可以看出在励磁调节器的作用下，计及发电机饱和后极限功率、极限功角均减小，发电机静态稳定性降低。

3 算例分析

3.1 同步发电机饱和对励磁电流调节量的影响

以图5中的a点作为发电机初始状态，此时的有功功率P=0.5，当发电机受到10%的有功功率扰动后，励磁调节器作用调节励磁电流以保持发电机暂态电势为恒定值，此时的发电机运行点由图6中的a点过渡到暂态功角曲线上。表3给出了扰动前后励磁电流的变化情况并与解析法计算结果进行了比较。

表3 小扰动后励磁电流调节量

从表3中可以看出计及同步发电机饱和作用后励磁电流的调节幅度更大，扰动前后差值达到6.17%，不计同步发电机饱和作用时差值只有3.7%。为了进一步分析不同运行状态时同步发电机饱和对励磁电流调节量的影响，计算了发电机满载时P=1.0，发电机受到10%的有功功率扰动后励磁电流的调节量，此时发电机运行与图5中的b点。由表3可以看出当发电机满载时,计及同步发电机饱和作用后，发电机的励磁电流调节量变大，扰动前后的相对差值达到6.36%。不考虑同步发电机饱和作用后，扰动前后励磁电流的相对差值减小到4.14%。

3.2 同步发电机饱和对励磁调节器放大系数的影响

根据式(13)推导的发电机静态稳定判据，利用1.4节中的方法分别计算计及与不计及同步发电机饱和作用时的励磁调节器放大倍数，结果如图8所示。

图8 放大系数最大允许值与运行角的关系Fig.8 The relation of power angle and maximum allowable value of amplification of excitation regulator

从图8中看出计及发电机饱和之后，在发电机功角δ>50°，励磁调节器出现了最大允许的放大倍数；不计饱和时在发电机功角δ>60°，励磁调节器出现了最大允许的放大倍数。为了说明放大系数最大允许值KAmax对发电机小扰动特性的影响，采用Prony[11,12]分析法得到了KAmax选取饱和值与不饱和值时的小扰动特性，并进行对比。图9给出了发电机初始功角δ0=80°，励磁调节器放大系数取KAmax时的小扰动特性指标。表4为通过Prony分析法得到的自然振荡频率和阻尼比等小扰动特性指标。从图9中可以看出当KAmax取不饱和值时发电机失去稳定，取饱和值时发电机处于临界失稳状态。说明传统解析法整定的放大系数极值偏大。表4的分析结果与图9的结果一致，KAmax取不饱和值时，系统状态方程的特征值出现正实部系统失去稳定。

图9 放大系数饱和值对小扰动角速度的影响Fig.9 Angular velocity with and without saturation of amplification of excitation regulator

表4 小扰动特性

3.3 同步发电机饱和对发电机运行极限的影响

以图5中的a点作为发电机初始状态，首先整定比例式励磁调节器的放大系数。根据文献[13]整定保证发电机暂态电势恒定时的励磁调节器的放大系数为KA=6.02。以KA=6.02作为励磁调节器放大系数的最大临界值，从图8中可以得到此时KA对应的极限功角，从图6中可以得到极限功角对应的极限功率。表4给出了计及与不计及饱和作用的发电机运行极限。

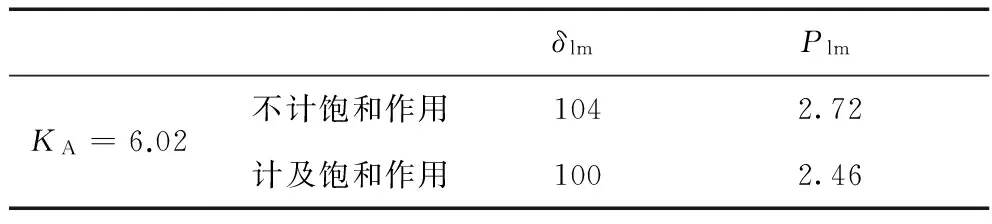
表5 发电机运行极限

从表4中可以看出计及饱和作用后的发电机运行极限变小，极限功角由104°变为100°，极限功率由2.72变为2.46，下降了9%。

综上所述，发电机饱和对励磁调节器的参数整定及发电机运行极限均有一定影响，在对发电机的静态稳定性进行研究时应当给予充分考虑。

4 结 论

本文提出了发电机3个端点量迭代的基于有限元法的功角特性计算方法，对比研究了同步发电机饱和及励磁调节共同作用下的静态稳定性。并得到以下结论：

(1)计及励磁调节器作用的发电机静稳极限要增大，但若同时考虑发电机饱和作用，静稳极限要有所减小。在励磁调节器保持暂态电势不变、初始功角为22°的情况下，计及与不计及发电机饱和作用后的极限功率相差14%，有限元法所得静态极限功角为110°，比解析法计算结果低3°。

(2)通过对比研究发电机发生小扰动后不同因素下励磁电流的调节量，得到发电机饱和及励磁调节器共同作用的励磁电流调节量要比不计饱和时的调节量大。当发电机满载、发生10%的有功功率扰动时，两者共同作用的励磁电流调节量达到了6.36%，不考虑发电机饱和时，调节量为4.14%。

(3)考虑发电机电机饱和后，运用有限元法计算的励磁调节器放大系数范围以及发电机运行极限均有所减小，发电机静态稳定域的范围减小。在对发电机的静态稳定性进行研究时应当充分考虑饱和作用的影响。本文以比例式励磁调节器作为励磁系统，没有考虑电力系统稳定器的作用，考虑更为详细的励磁系统模型后，发电机饱和作用对其静态稳定性的影响尚需进一步研究。

[1] 刘取. 电力系统稳定性及发电机励磁控制[M].北京:中国电力出版社,2007.

[2] 罗应立,张新丽,康锦萍,等. 汽轮发电机非线性特征的机理及其与运行条件的关系[J]. 中国电机工程学报,2008,28(17):144-150.

[3] 罗应立,蒙亮,刘晓芳,等. 汽轮发电机双因素非线性特性的研究[J]. 电工技术学报,2005,20(6):1-5.

[4] 康锦萍,刘晓芳,罗应立,等. 汽轮发电机磁路饱和与磁场畸变共同作用对运行的影响[J]. 中国电机工程学报,2010,30(36):41-45.

[5] 康锦萍. 考虑饱和与磁场畸变的汽轮发电机运行行为的研究[D]. 北京：华北电力大学,2010.

[6] 晁晖,李志强,罗应立,等. 同步电机场路耦合端点量迭代新算法[J]. 中国电机工程学报,2009,29(30):63-69.

[7] 李志强,胡笳,祝丽芳,等. 同步发电机有限元磁场计算中端点量迭代的改进算法[J]. 电工技术学报,2008,23(12):35-41.

[8] 陈为贤. 300MW机组励磁控制简介及其进相运行分析[J]. 江苏电机工程,2007,26(3):64-66.

[9] 吴学苹,江宁强. 交直流电力系统暂态过程中同步发电机阻尼转矩系数的计算[J]. 电气技术,2015,16(8):11-14+33.

[10] 丁建顺,王青,马世英,等.发电机叠加型低励限制对电力系统动态稳定影响机制[J].电力系统自动化,2016,40(8):78-84+91.

[11] 许国瑞,刘晓芳,罗应立,等. 汽轮发电机转子阻尼系统对小扰动特性的影响[J]. 华北电力大学学报(自然科学版),2014,41(2):20-27.

[12] 曹维,翁斌伟,陈陈. 电力系统暂态变量的Prony分析[J]. 电工技术学报,2000,15(6):56-60.

[13] 何仰赞,温增银. 电力系统分析(下)[M]. 武汉:华中科技大学出版社,2002.

Static Stability of Synchronous Generator Considering Generator Saturation and Excitation Regulation

GUO Shuai1，KANG Jinping1，XU Guorui1，ZHANG Zhijian2

(1.School of Electrical and Electronic Engineering，North China Electric Power University，Beijing 102206，China；2.State Grid Beijing Electric Power Company，Beijing 100031，China)

In order to research the influence of generator saturation and excitation regulation on static stability of synchronous generator, this paper presents a new finite element algorithm of power-angle curve with the effect of excitation regulator. The effect of generator saturation and excitation regulation on limit power of generator and limit power-angle has been analyzed. The power-angle curve calculated by the proposed algorithm can be used to determine the limit value of the amplification of excitation regulator after small disturbance and the operation limit of generator. The results show that the limit of static stability will increase with the effect of excitation regulator; however, it will decrease when generator saturation is also taken into consideration. If there is small disturbance, amplification of excitation regulator will decrease significantly with the consideration of synchronous generator saturation. And the regulating quantity of exciting current will increase. The results provide necessary theoretical foundation for parameter tuning of excitation regulator and system dynamic simulation.

turbine generator; magnetic saturation; finite element; power-angle curve; static stability

10.3969/j.ISSN.1007-2691.2017.01.09

2016-05-10.

国家自然科学基金资助项目(51307049).

TM311

A

1007-2691(2017)01-0058-07

郭帅(1992-)，男，硕士研究生，研究方向为发电机磁场数值分析计算。