分数阶双二次型导抗函数的无源综合

荆永明，梁贵书，赵海成

(1.华北电力大学 电气与电子工程学院, 河北 保定 071003； 2.山西耀光煤电有限责任公司，山西 晋中 031100)

分数阶双二次型导抗函数的无源综合

荆永明1，梁贵书1，赵海成2

(1.华北电力大学 电气与电子工程学院, 河北 保定 071003； 2.山西耀光煤电有限责任公司，山西 晋中 031100)

无源网络综合一直是备受关注的研究课题，近几年，随着分数阶微积分的广泛应用，人们开始研究含有分数阶阶次的策动点函数综合。基于三口纯电阻网络与两个分数阶储能元件的连接，提出了分数阶双二次型导抗函数最少储能元件无源综合方法。推导了其实现的充分必要条件。此外，对于无法用电阻矩阵表示三口电阻网络的情况，通过相应的串并联电路得到其实现条件及对应元件值。当两个分数阶阶次均为1时，所提方法可退化为传统双二次型导抗函数综合，因而具有更广的应用范围，最后，通过数值例子验证了所提方法的准确性。

分数阶双二次导抗函数；三口电阻网络；网络综合

0 引 言

近些年，分数阶电路和系统已广泛应用于不同实际工程中。分数阶电子电路的研究包括其稳定性分析[1]、时域响应分析[2]、频域响应分析[3]、能源效率分析[4]、共振条件分析[5]和灵敏度分析[6]。对于分数阶电路的综合，传统思路是通过整数阶方法逼近分数阶系统，再对其进行物理实现[7,8]。然而，因整数阶元件不能直接体现分数阶阶特性，逼近时所需元件数较多，结构复杂。目前，已有不同方法搭建分数阶电容器和电感器[9,10]，基于这些电子元件，分数阶系统可以简单精确地实现[11]。因此，研究基于分数阶元件的无源网络综合具有至关重要的意义。然而，分数阶网络函数很难有一般的实现方法，文献[12]通过RLC双口网络与分数阶电容连接，在一定条件下可以综合分数阶策动点阻抗函数。

(1)

1 一般分数阶策动点导纳函数的实现

1.1 电路结构

欲通过三口电阻网络与分数阶储能元件的连

接实现如式(1)分数阶双二次导纳函数。因不同类型储能元件的连接可实现更广的网络函数，所以采用一个分数阶电容和一个分数阶电感与三口电阻网络的连接方式进行综合，如图1所示。

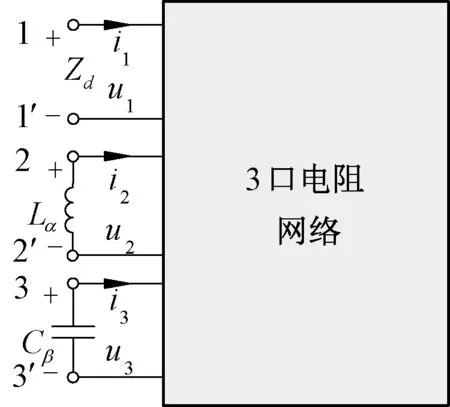
图1 三口电阻网络与分数阶储能元件连接Fig.1 Three port resistive network connected with fractional energy storage elements

纯电阻网络为基本网络，端口2接α阶电感，端口3接β阶电容。三口纯电阻网络电阻矩阵为

(2)

(3)

(4)

其中，

将R矩阵转换可得X矩阵，转变过程如式(5)

(5)

其中，X为半正定矩阵，且

(6)

则式(3)可以转化为式(4)。

1.2 分数阶策动点导纳函数实现

给定如式(1)策动点导纳函数，首先需转换为式(4)含有X系数的导纳函数，得到半正定矩阵X，再转为式(3)含有Rij(i,j=1,2,3)系数的导纳函数，得到Paramount矩阵R。最后，根据Tellegen电路实现矩阵，根据k，b确定分数阶电容和分数阶电感值，即可得到图1电路结构。

1.2.1 导纳函数系数应满足的条件

定理1：根据文献[13]定理4的思路可得，给定一般的分数阶策动点导纳函数如式(1)所示，其可以转换为式(4)的条件为

(7)

(8)

(9)

X3=a0X2

(10)

(11)

(12)

d1≥a1

(13)

a0d1-d0a1≥0

(14)

a0≥a1a2

(15)

(16)

(17)

1.2.2 导纳函数的实现

式(4)对应的系数为X矩阵，当且仅当其可以转化为式(3)，且对应R为Paramount矩阵[13]，k>0，b>0，才能通过图1的方式实现。下面讨论式(4)应满足的条件。

文献[13]中的引理1和引理2介绍并证明了半正定矩阵X转换为Paramount矩阵R应满足的条件，本文不再赘述。

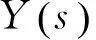
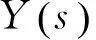
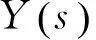
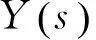
1.2.3 综合示例

考虑式(18)分数阶双二次型导纳函数的实现。

(18)

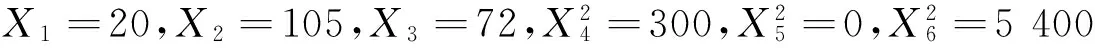
(19)

(20)

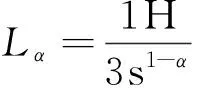
图2 式 (18)电路实现结构Fig.2 Circuit for equation (18)

2 特殊分数阶策动点导纳函数的实现

上文给出了采用两个分数阶元件和电阻组成网络实现策动点导纳函数的一般实现方法，对于符合相应条件的导纳函数，可按照上述流程进行综合。然而，当三口Tellegen电路(如图3所示)的某一元件值为无穷大时，式(2)电阻矩阵R无法表示，上述方法失效。尽管可用其对偶矩阵G求解，本文针对特殊情况提出了更简单综合方法。

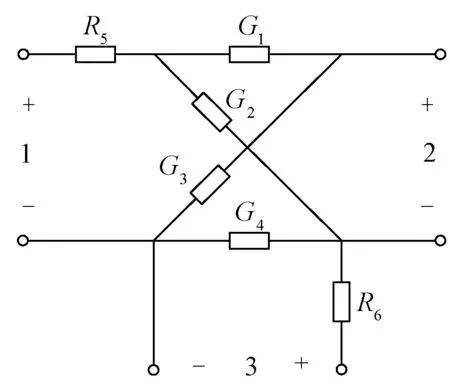
图3 电阻R矩阵对应Tellegen电路Fig.3 Tellegen circuit corresponding to matrix R

2.1 特殊网络结构分类

图3中，为了不短接端口2的分数阶电感，G1和G2不能同时为无穷大；为了不短接端口3的分数阶电容，G4不能为无穷大。因此，特殊情况的串并联电路可分为两大类，8种对应电路，如表1所示。

表1 不能用R矩阵表示三口电阻网络

Tab.1 Three port resistive circuits which cannot be expressed by matrixR

特殊三口电路结构分类G1=∞,G2=0①G3=G4=0②G3=0,0

2.2 特殊结构实现的充分必要条件

针对每种电路，推导了其实现的充分必要条件及相应元件值，以②号电路为例，过程见定理5。

(21)

图4 G1=∞、G2=0、G3=0、0

其他7种策动点导纳函数所对应的电路结构及其可以实现的充分必要条件汇总如表2(见附录)。

2.3 综合示例

考虑式(22)分数阶双二次型导纳函数的实现。

(22)

图5 式(22)的电路实现结构Fig.5 Circuit for equation (22)

3 结 论

本文提出了分数阶双二次型导抗函数的最少储能元件综合方法，即通过三口电阻网络与分数阶电容和分数阶电感连接进行实现，推导了其实现的充分必要条件。此外，对于无法用电阻矩阵表示三口电阻网络的情况，通过相应的串并联电路得到其实现条件及对应元件值。最后通过示例验证了所提方法的准确性。当阶次α=β=1时，此方法可退化为传统双二次导抗函数的综合，因而具有更宽的应用范围，为分数阶无源网络综合提供了新方法。

[1]RADWANAG,Stabilityanalysisofthefractional-ordercircuit[J].FractionalCalculusAppl,2012,3(1): 1-13.

[2]JACYNTHOLA,TEIXEIRAMCM,ASSUNCAOE,etal.Identificationoffractional-ordertransferfunctionsusingastepexcitation[J].CircuitsandSystemsII:ExpressBriefs,IEEETransactionson, 2013, 62(9): 896-900.

[3]GALVORKH,HADJILOUCASS,KIENITZKH,etal.Fractionalordermodelingoflargethree-dimensionalRCnetworks[J].CircuitsandSystemsI:RegularPapers,IEEETransactionson, 2013, 60(3): 624-637.

[4]HARTLEYTT,VEILLETTERJ,ADAMSJL,etal.Energystorageandlossinfractional-ordercircuitelements[J].Circuits,Devices&Systems,IET, 2013, 9(3): 227-235.

[5]RADWANAG.Resonanceandqualityfactorofthefractionalcircuit[J].EmergingandSelectedTopicsinCircuitsandSystems,IEEEJournalon, 2013, 3(3): 377-385.

[6]DIAOLJ,ZHANGXF,CHENDY.Fractional-ordermultiplecircuit[J].ActaPhysicaSinica, 2014,63(3): 038401.

[7]MAIONEG.Closed-formrationalapproximationsoffractional,analoganddigitaldifferentiatorsintegrators[J].EmergingandSelectedTopicsinCircuitsandSystems,IEEEJournalon, 2013, 3(3): 322-329.

[8]MAIONEG.Laguerreapproximationoffractionalsystems[J].ElectronicsLetters, 2002, 38(20): 1234-1236.

[9]KRISHNAMS,DASS,BISWASK,etal.Fabricationofafractionalordercapacitorwithdesiredspecifications:Astudyonprocessidentificationandcharacterization[J].ElectronDevices,IEEETransactionson, 2011, 58(11): 4067-4073.

[10]MONDALD,BISWASK.PackagingofSingleComponentFractionalOrderElement[J].DeviceandMaterialsReliability,IEEETransactionson, 2013, 13(1): 73-80.

[11]TAVAZOEIMS,TAVAKOLI-KAKHKIM.Minimalrealizationsforsomeclassesoffractionalordertransferfunctions[J].EmergingandSelectedTopicsinCircuitsandSystems,IEEEJournalon, 2013, 3(3): 313-321.

[12]SARAFRAZMS,TAVAZOEIMS.RealizabilityofFractional-OrderImpedancesbyPassiveElectricalNetworksComposedofaFractionalCapacitorandRLCComponents[J].CircuitsandSystemsI:RegularPapers,IEEETransactionson, 2013, 62(12): 2829-2835.

[13]CHENMZQ,SMITHMC.Electricalandmechanicalpassivenetworksynthesis[M].RecentAdvancesinLearningandControl.SpringerLondon, 2008: 35-50.

[14] 王锴, 陈志强. 双二次阻抗函数的低复杂度实现问题 [C].第 24 届中国控制与决策会议论文集. 2012.

附录

Passive Synthesis of Fractional Biquadratic Immittance Function

JING Yongming1， LIANG Guishu1，ZHAO Haicheng2

(1.School of Electrical and Electronic Engineering, North China Electric Power University, Baoding 071003,China;2.Shanxi Yaoguang Coal & Power Limited Liability Company, Jinzhong 031100,China)

Passive network synthesis is a research topic which has been a focus one. In recent years, with the wide application of fractional calculus, researchers began to study and analyze the driving-point function synthesis containing fractional order. The passive synthesis method which contains minimal energy storage element for fractional biquadratic immittance function is proposed based on the connection of three-port pure resistive network and two fractional order storage elements. The necessary and sufficient conditions for the realization of the proposed method are deduced. In addition, if the three-port pure resistive network cannot be represented by resistance matrix, the realization condition and corresponding component values can be obtained by relevant series-parallel circuit. When the both orders are equal to 1, the proposed method degenerates into traditional biquadratic immittance function synthesis, which indicates it has wider application. At last, the proposed method is verified by numerical examples.

fractional biquadratic immittance function; three-port resistive network; network synthesis

表2 特殊分数阶双二次策动点导纳函数的实现结构、实现条件及对应元件值

Tab.2 Synthesis structure, realization condition and component values for special fractional biquadratic driving-point admittance function

编号对应网络函数实现结构元件值与系数间关系满足条件①Ys()=CsβEsα+β+Gsβ+HLα=EC,Cβ=CH,R6=GCC、E、H>0,G≥0,当G=0时,R6=0②Ys()=Csβ+DEsα+β+Fsα+Gsβ+HLα=EC,Cβ=CH-DGH2,G4=DH,R6=GHCH-DGC、D、E、F、H>0,G≥0DE=CF,CH-DG>0,当G=0时,R6=0③Ys()=Asα+β+Csβ+DEsα+β+Gsβ+HLα=EHCH-DG,Cβ=CH-DGH2,G3=DH,R6=FGAH-BGA、C、D、E、H>0,G≥0,AH=DE,CH-DG>0AH-BG>0,当G=0时,R6=0④Ys()=Asα+β+Bsα+Csβ+DEsα+β+Fsα+Gsβ+HLα=F2DF-BH,Cβ=DF2G-BEGH-BCFGCF2H,G3=BFG4=DF-BHHF,R6=CF2DF2-BEH-BCFA、C、D、E、H>0,G≥0ABFH2+BDEFH+BDF2G=ADF2H+B2EH2+2B2FGHDEFH+DF2G=CF2H+BEH2+DF2GDF2G-BEGH-BCFG>0,DF-BH>0DF2-BEH-BCF>0,当G=0时,R6=0⑤Ys()=Asα+β+Bsα+Csβ+DEsα+β+FsαLα=FD,Cβ=AD-BCDF,G4=BF,R6=EFAF-BEA、B、D、F>0,C、E≥0DE=CF,AF-BE>0,AD-BC>0当C=E=0时,R6=0⑥Ys()=Asα+β+Csβ+DEsα+β+FsαLα=FD,Cβ=AF,R6=EAA、D、F>0,C、E≥0DE=CF,当C=E=0时,R6=0⑦Ys()=Asα+β+Csβ+DEsα+β+Fsα+Gsβ+HLα=FD,Cβ=AF,G3=DH,R6=FGAHA、C、D、F、H>0,E、G≥0AEH2+DEFG=CF2G,FG=HE当E=G=0时,R6=0⑧Ys()=Asα+β+Bsα+Csβ+DEsα+β+Fsα+Gsβ+HLα=F2DF-BH,Cβ=AH-BGHFG3=DF-BHHF,G4=BF,R6=FGAH-BGA、C、D、F、H>0,E、G≥0AEH2+DEFG=BEGH+CF2G,FG=HEAH-BG>0,DF-BH>0当E=G=0时,R6=0

10.3969/j.ISSN.1007-2691.2017.01.07

2016-05-16.

国家自然科学基金资助项目(51177048)；河北省自然科学基金资助项目(E2012502009).

TN711.1

A

1007-2691(2017)01-0046-06

荆永明(1987 -)，男，博士研究生，研究方向为电网络理论及其在电力系统中的应用；梁贵书(1961 -)，男，教授，主要研究方向为电网络理论及其应用，电力系统电磁兼容和电力信息分析与处理等。