车辆磁流变半主动悬架模糊滑模控制★

王 瑞

(1.合肥工业大学机械工程学院，安徽 合肥 230009； 2.安徽交通职业技术学院，安徽 合肥 230051)

车辆磁流变半主动悬架模糊滑模控制★

王 瑞1，2

(1.合肥工业大学机械工程学院，安徽 合肥 230009； 2.安徽交通职业技术学院，安徽 合肥 230051)

为提高半主动悬架减振效果，将结合模糊控制理论的滑模控制算法应用于磁流变半主动悬架控制中，并通过Matlab/Simulink建立了磁流变阻尼器及悬架动力学模型，同时进行了仿真分析，结果表明，采用模糊滑模控制策略优于传统控制策略。

磁流变，半主动控制，半主动悬架，滑模控制，模糊控制

0 引言

主动悬架结构复杂，成本高，而半主动悬架结构简单，成本低，控制效果接近主动控制悬架，故在近些年得到广泛关注[1-3]。磁流变阻尼器是一种以磁流变液为减振液的半主动阻尼器，可改变控制电流使阻尼适应路况的变化，从而改善悬架的减振效果。

为准确描述磁流变阻尼器的动态特性，在Matlab/Simulink中建立磁流变阻尼器的Bingham模型。将天棚控制方法、滑模控制方法及模糊滑模控制方法应用到磁流变半主动悬架控制中，在Matlab/Simulink中建立磁流变半主动悬架控制模型并进行仿真，对比验证了模糊滑模控制方法在半主动悬架控制中的优越性。

1 磁流变阻尼器动力学模型

1.1 磁流变阻尼器的Bingham模型

Stanway提出的非线性Bingham模型，可用于描述磁流变阻尼器的动态特性[4]。

(1)

对式(1)进一步推导可得阻尼力—位移关系式。

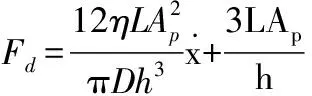
(2)

其中，L为活塞有效长度；D为缸体内径；Ap为活塞有效面积；h为孔道直径；τy为与磁场强度有关的磁流变液屈服应力。

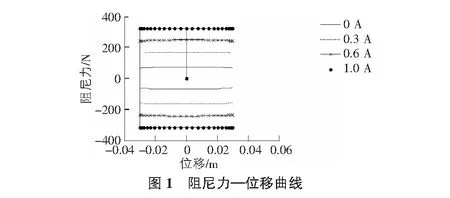
在Simulink中对式(2)进行建模，采用正弦激励，阻尼器力—位移曲线及阻尼力—速度曲线如图1，图2所示。仿真结果表明，MR阻尼器阻尼力随电流增大而增大，阻尼力与速度具有非线性关系。由图可看出阻尼器刚度不可调，阻尼器阻尼为变化值，即阻尼系数可调。

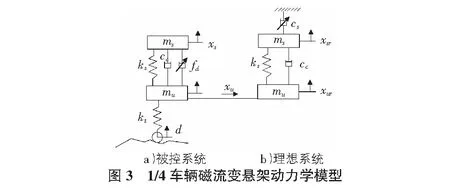
1.2 磁流变半主动悬架模型

如图3所示，建立2自由度1/4车辆磁流变悬架动力学模型[5]，动力学方程为：

(3)

2 控制系统模型

2.1 天棚控制

根据天棚控制理论[6]，其阻尼力大小为：

(4)

2.2 理想控制模型

以簧下质量状态作为理想控制模型的输入，动力学方程为：

(5)

其中，

(6)

2.3 滑模控制器设计

使系统簧上质量运动跟踪理想模型簧上质量运动，定义误差矢量：

(7)

状态方程：

(8)

取滑模面：

s=c1e1+e2

(9)

进一步得到：

(10)

取等速趋近律：

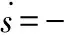
(11)

控制率为：

fdeq=-kse1+(msc1-cc)e2+c0xr2+msεsgn(s)

(12)

故半主动悬架控制力为：

(13)

2.4 模糊滑模控制器设计

上述滑模控制器中采用等速趋近律，参数ε取恒定值，系统距离滑模面较远时，若ε增大，有助于系统能够快速的到达滑模面，而当系统距离滑模面较近时，若ε减小，有助于防止系统抖振的发生。即：

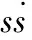
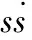
3 仿真分析

为验证模糊滑模控制器的控制效果，在Matlab/Simulink中对悬架控制系统进行了数值仿真，以正弦信号作为输入信号，簧上质量位移仿真结果见图6，图7，簧上质量振动加速度仿真结果如图8，图9所示。由图6，图7可以看出，磁流变半主动控制悬架的减振效果比被动悬架减振效果更好，天棚控制由于利用开环控制，没有对阻尼力的误差进行反馈控制，导致减振效果与理想控制模型效果相差较多，使被控系统簧上质量运动跟踪理想模型簧上质量运动的滑模控制悬架，采用了闭环控制，对阻尼器的误差进行了反馈弥补，故控制效果接近于理想模型。从图8，图9可以看出，磁流变阻尼器半主动悬架的簧上质量加速度明显低于被动悬架簧上质量加速度，且模糊滑模控制悬架由于对趋近参数ε进行了模糊控制，降低了系统到达滑模面时的抖动，故模糊滑模控制簧上质量加速度更小，控制效果更好。

4 结语

在Matlab/Simulink中建立了磁流变阻尼器半主动控制悬架的天棚控制、滑模控制、模糊滑模控制模型，设计了简单易于实现的模糊滑模控制器。数值分析表明，采用模糊滑模控制的半主动减振系统的车身振动位移、振动加速度都得到了有效的抑制，控制效果明显，且克服了滑模控制系统到达滑模面时易抖动的缺点。

[1] 王其东，王祺明，陈无畏.磁流变半主动悬架变论域模糊控制研究[J].机械工程学报，2009,22(5):512-518.

[2] Wang D H, Liao W H. Magnetorheological fluid dampers: a review of parametric modelling[J].Smart Materials & Structures,2011,20(2):439-445.

[3] 廖昌荣,余 淼,陈伟民,等.汽车磁流变减振器设计原理与实验测试[J].中国机械工程,2002,13(16):1391-1394.

[4] Stanway.R, Sproston J L. Nonlinear Modeling of an Electrorheological Vibration Damper[J].Journal of Electrostatics,1987(2):167-184.

[5] 姚嘉凌,郑加强,蔡伟义.车辆半主动悬架模型参考滑模控制[J].农业机械学报,2008,39(4):5-8.

[6] Karnopp D, Crosby M J, Harwood R A. Vibration control using semi-active force generators[J].Journal of Engineering for Industry,1974(96):619-626.

[7] 具有非线性时滞的汽车磁流变悬架系统自适应模糊滑模控制[J].振动与冲击，2009,28(11):55-60.

[8] 石辛民，郝整清.模糊控制及其MATLAB仿真[M].北京：清华大学出版社，北京交通大学出版社，2008:149-165.

Advanced fuzzy sliding mode control of automobile semi-active suspension with magneto-rheological dampers system★

Wang Rui1,2

(1.MechanicalEngineeringSchool,HefeiUniversityofTechnology,Hefei230009,China; 2.AnhuiCommunicationsVocational&TechnicalCollege,Hefei230051,China)

To improve the performance of vibration isolation of automobile semi-active suspension, models of semi-active suspension and magnetorheologicaI damper are built by Matlab/Simulink. The advanced fuzzy sliding mode logical theory is applied on semi-active suspension．The results of analysis and comparison imply that advanced fuzzy sliding mode strategy is better than others.

magnetorheological, semi-active control, semi-active suspension, sliding mode, fuzzy control

1009-6825(2017)03-0221-02

2016-11-15

王 瑞(1986- )，男，硕博连读研究生，助教

U464.12

A

★：安徽省教育厅《高等职业教育创新发展行动计划(2015—2018)》项目，项目类别：XM-01，项目名称：工程机械运用技术