流化床内颗粒与流体间传热研究进展*
2017-03-15王伟文谢建照董纪鹏张自生
王伟文,谢建照,董纪鹏,张自生**
(1.青岛科技大学 化工学院,山东 青岛 266042;2.青岛科大隆腾科技发展有限公司,山东 青岛 266042)
从第一台流态化工业装置Winkler煤气化炉出现至今,对流态化技术的研究已有近百年历史。流化床因气-固两相接触面积大、传热传质速率快、温度梯度小,被广泛应用于干燥、制粒、药物包衣、多晶硅制备等领域[1-4]。流化床内的传热研究始于20世纪50年代,流化床内的传热一般包括四个方面:从床层到内浸表面(包括床壁面及内构件表面)的传热;流体与固体颗粒间的传热;固体颗粒内的传热;颗粒与颗粒间的传热。近年来,在床层与内浸面传热领域的研究有大量文献发表[5-7],但是颗粒与流体间传热的实验研究仍停留在20世纪70年代水平。
在流化床反应与流化床干燥过程中,颗粒与流体间的传热过程显得尤为重要。如刘安源[8]使用离散相模型进行流化床内部传热数值模拟时发现,颗粒与流体间的传热量约占颗粒总传热量的66%。Rantz[9]根据大量的实验数据得出单个颗粒的气-固传热系数关联式,Kunii[10]等研究者也得到了不同形式的颗粒与流体间的表观传热系数(以床层内所有颗粒表面积为有效传热面积计算得到的传热系数)关联式。但Kunii[10]进行粗颗粒的流化床实验时发现,当颗粒雷诺数大于100时,流化床中颗粒与流体间的表观传热系数大于Rantz[9]关联式给出值;对于颗粒雷诺数远小于100的细颗粒,在流化床中颗粒与流体间的表观传热系数远小于单个颗粒的气-固传热系数的理论最小值。由于不同研究者得出的流化床中颗粒与流体间传热系数实验结果差异甚大,而且流化床中的表观传热系数远低于单颗粒的气-固传热系数理论最小值,研究者也试图从传热机理上寻求解释。作者综述了目前研究者进行颗粒与流体间传热研究时采用的实验方法、形成的传热机理和数值模拟中常采用的传热关联式。
1 研究方法
1.1 稳态传热实验方法
在稳态传热实验方法中,通常假设气体和颗粒温度在起始时都是均匀的,穿过床层的气体为活塞流,通过壁面的传热或添置新鲜冷(热)颗粒来保持床层的热稳定状态,固体颗粒在床层中为理想混合,径向上颗粒保持均一的温度。此时,除了气体入口周围一个很小区域外,床层其它区域均处于同一温度,因此,采用这种方法的研究者[11]常常测定邻近床层入口处气体温度的变化,来求取传热系数。通常情况下,流体温度可采用裸露或带隔离固体颗粒细网的热电偶测定,固体颗粒温度的测定一般采用间接估计的方法,如置于塌落床层的裸露热电偶测定。
设固体颗粒在床层中理想混合,并不计热损失,对床高为dl的微元进行气体的热衡算得到:
-cpgGgdT=ha(T-ts)dl
(1)
式中,cpg为气体比热容,J/(kg·K);Gg为气体表观质量流速,Gg=uρg,kg/(m2·s);T为气体温度,K;h为传热系数,W/(m2·K);a为床层颗粒比表面积,m2/m3;ts为颗粒温度,K。
在气体活塞流、固体颗粒全混流的假设条件下,积分式(1)得:
(2)
式中,在半对数坐标系中,由该温度函数对床高的关系曲线的斜率可求得传热系数h。
1.2 非稳态传热实验方法
采用非稳态传热实验方法的研究者[12]考虑到床层温度处处均一,出口处的温度随时间变化,通过测得气体在进、出口处的温度,根据床内气、固热量衡算可得到颗粒在任何时间的温度,在忽略热量损失的条件下,气体通过床层失去的热量等于颗粒获得的热量,求得床层平均传热系数,整个床层的热衡算有:
cpgGg(Tin-Te)=haL(T-ts)
(3)
在不稳定状态下,流化床进口气体温度已知,出口温度则随时间改变,假定气体在床层内完全混合,气体为返混流。若不计气体累积热,对床层任一微元高度dl作热衡算得到:

(4)
式中,dω为微元dl中固体颗粒的质量,kg。
微分式(3)代入式(4)消去ts,然后积分得到:
(5)
在颗粒与流体的传热实验中,基于返混流的非稳态实验结果极为分散,且随床高有一系统性的趋向;而基于活塞流假设的稳态传热实验结果,则有一致的趋势,并可关联成经验关联式。这表明在流化床内颗粒与流体传热的分析中,气体活塞流假设较返混流假设更有意义。
1.3 热频率响应实验方法
流化床中不同颗粒与流体间传热的实验结果差异大,其原因除传热面积的界定较为困难外,颗粒与流体温度测量不精确且方法各异,尤其是颗粒温度的测量。因为流化床内置热电偶指示的温度不能确定是颗粒温度还是气体温度,随着颗粒对热电偶前端碰撞频度不同,在两个温度之间不稳定地变化,使得传热实验结果有较大误差。由于热响应实验方法,无需测量床层及颗粒温度,从而可以避免因温度测量不精确带来的实验误差。即采用气体温度脉冲(正弦式[13-14]、方波式[15]和脉冲式[16]等)来激发系统的动态特性,通过测定表征动态特性的系统瞬态温度响应,来研究系统的传热。
1.4 数值模拟法
目前对流化床内部传热规律的研究尚不充分,不能满足工业设计要求。随着计算机运算速率的大幅提高和流体力学数值模拟方法在多相流领域的应用,研究者[17-19]使用考虑了颗粒与颗粒间及颗粒与流体间相互作用的离散相模型对流化床内气固两相流动、传热和反应过程进行数值模拟。离散单元方法充分考虑了颗粒运动规律(平动和转动)、颗粒与流体间作用力和颗粒之间碰撞,并且模拟过程可进行颗粒水平的能量、动量分析,而这些参数在气固两相流实验中是不能精确测量的。其中,数值模拟过程中颗粒与流体间的传热模型多基于Kunii模型[10]。刘安源[8]在模拟密相流化床内传热过程的研究中发现:示踪颗粒在流化床内具有较高的传热系数,与示踪颗粒与周围颗粒碰撞次数有关,但与示踪颗粒在流化床内的位置无关;在颗粒与床层传热总量中,颗粒碰撞传热量约占1/3,与周围流体的对流传热量约占2/3。
2 颗粒与流体间的传热机理
对于流化床内不同颗粒与流体间传热实验研究结果差异甚大和传热系数远远低于单颗粒的传热系数理论最小值的现象,研究者给出了多种传热机理予以解释。
Zabrodsky[20]提出的微隙模型认为,超出临界流化需要量以外的剩余气体,短路通过一排或数排固体颗粒,然后再与穿过床层的气体完全混合,在气体通过床层时,此过程不停重复进行。由于流化床内颗粒的不稳定团聚(分子力或静电力所致),减弱了连续相和非连续相之间气体交换强度,使气体在通过颗粒后达不到完全的径向混合,气体温压也大为降低,从而导致很小的颗粒与流体间的传热系数。
Pfeffer[21]则提出了一种自由表面模型,以及基于该模型的能量方程。模型假设颗粒与流体系统是由许多“微元”组成的随机系统,每一个 “微元”均含有由流体包络环绕的颗粒及相同的流体。“微元”是一个外表面无摩擦或有自由表面的球体,假设“微元”边界的温度为流体温度。基于这一模型的能量方程的求解结果表明,颗粒床层的平均努赛尔数是空隙率和普朗特数的函数。
Kunii和Levenspiel[10]提出的流化床模型指出,在满足u>2umf(umf为流化床的最小流化气速)的条件下,流化床可分为气泡相和乳化相两个区域。乳化相处于临界流化状态,气泡相中基本没有固体,只有迅速运动的气泡被气泡晕和相随而来的尾涡所包围,气泡晕和尾涡中夹带的颗粒以及气泡在上升汇并的过程增加了与颗粒的接触,造成了气体与颗粒间的传热。
在各种传热模型中,只是强调了不同参数或基于不同的假设,借以分析颗粒与流体间传热过程。然而实际的传热过程要复杂的多,流化床的结构及床内流动状态对传热的影响又不可忽略,因而还没有一个模型将已有的实验数据统一起来成为普遍化的关联。同时,对流化床内颗粒与流体间流动特性的深入研究是分析传热机理的基础,可视化检测技术(如正负电子成像技术[22]、核磁共振成像[23-24]和过程层析成像技术[25-26]等)在流化床研究中的应用与发展,使对流化床内颗粒运动探测更加准确,有助于提高对流化床中传热机理的认识。
3 传热系数关联式
处理实验数据不同的模型假设及颗粒温度测定困难,导致颗粒与流体间传热的实验结果差异很大,难以获得统一的关联式。对于密相流化床中的传热,应用较为广泛的关联式有以下几种[27-29]。
Kunii和Levenspiel[10]假设流化床中气体与颗粒混合完全,气体运动为活塞流,将单颗粒与气体的传热关联式应用到流化床中,通过实验数据检验回归得到:
Nui=0.03Rei1.3
0.1 Re>100 (7) 根据Kunii和Levenspiel的建议,b=0.5;根据流化床的操作情况数值a=0.6~1.8。此传热模型在基于欧拉-拉格朗日方法的气固两相流数值模拟中得到了广泛应用,在不同的离散相数值模拟中a设定在约1.2[30]。 在此基础上,Kato等[31]进一步考虑到床高对气、固之间运动与传热的影响,把流化床沿高度分为若干段,然后逐段进行回归,得到如下关联式: Nui=0.59Rei1.1(di/Lb)0.9 (8) 式中,Lb是流化床床层高度。 Gunn[32]采用热响应实验方法,通过研究床层对脉冲式温度变化的动态响应,提出床层空隙率在0.35~1,固定床和流化床颗粒与流体间表观传热系数表达式: (9) 此关联式与Wakao[33]等在固定床中得到的实验数据吻合,在基于欧拉-欧拉模型的气固两相流数值模拟中,多采用考虑了床层空隙率的气固传热模型。 Gelperin-Einstein[34]气固传热系数模型与Guun模型的共同点是也包含了空隙率: 郭雪岩等[35]采用欧拉-欧拉模型对GeldartD类颗粒气固流化床的非定常传热过程模拟中,比较了Gunn模型在内的6种不同气固传热系数模型。基于这6种气固传热模型得出的平均壁面传热系数与文献[28]中实验关联式给出值基本一致,但是6种模型给出的局部气固传热系数呈现较大的差别,由于没有局部尺度的实验数据对照,对使用不同气固模型的模拟结果难以评估。 对于颗粒与流体间的传热过程,国内外学者由大量实验数据已检验回归出多种颗粒与流体间的传热系数关联式,并应用到数值模拟及工业设计过程中。但对流化床内部传热规律的研究仍不充分,因此,十分必要寻求准确反映流化床气固流动与传热的新准则数。有关流化床气固传热的实验研究仍停留在20世纪70年代水平,实验方法及手段有待改进。在颗粒的运动规律以及区域颗粒运动对颗粒与流体间传热的影响的研究方面主要为数值模拟,相关的实验研究鲜有报道。随着先进可视化测试技术的发展,对颗粒运动的观测成为可能,流化床内颗粒运动规律研究有助于更深入地认识颗粒与流体间传热机理。 [1] 韩树晓,向飞,王月,等.煤的内热流化床干燥实验研究[J].煤炭转化,2014,37(1):28-31. [2] 杨佳静,杨云松,李银,等.胃苏颗粒流化床制粒工艺的研究[J].现代中药研究与实践,2015,29(6):41-42. [3] 王文喜,朱淼,高捷,等.多索茶碱脉冲微丸的制备及释药机制研究[J].浙江工业大学学报,2016,44(3):346-350. [4] 李超杰,王伟文,张自生.流化床法制备多晶硅过程研究进展[J].当代化工,2015,44(9):2235-2238. [5] 张瑞卿.涵盖不同流型的气固床层与壁面换热研究[D].北京:清华大学,2014. [6] 晁俊楠,吕俊复,杨海瑞,等.流化床内自由移动石墨球表面的传热系数[J].化工学报,2014,42(8):2869-2875. [7]ABDELMOTALIBHM,YOUSSEFMAM,HASSANAA,etal.Heattransferprocessingas-solidfluidizedbedcombustors:Areview[J].InternationalJournalofHeatandMassTransfer,2015,89:567-575. [8] 刘安源.流化床内流动-传热及燃烧特性的离散颗粒模拟[D].北京:中国科学院工程热物理研究所,2002. [9]RANZW,MARSHALLW.Evaporationfromdrops[J].ChemicalEngineeringProgress,1952,48:141-146. [10]KUNIID,LEVENSPIELO.Fluidizationengineering[M].Amsterdam:Elsevier,2013:257-274. [11] 刘彬,原如冰,张强,等.发酵柑桔皮渣流化干燥传热传质分析[J].农业工程学报,2011,27(7):353-357. [12]SUNKOORIN.KAPARTHIR.Heattransferstudiesbetweenparticlesandliquidmediuminafluidizedbed[J].ChemicalEngineeringScience,1960,12:166-174. [13]BRODKEYR.Fluidtoparticleheattransferinafluidizedbedandtosingleparticles[J].InternationalJournalofHeatandMassTransfer,1991,34:2327-2337. [14]LINDAUERGC.Heattransferinpackedandfluidizedbedsbythemethodofcyclictemperaturevariations[J].AIChEJournal,1967,13(6):1181-1187. [15]LITTMANH,STONEAP.Gas-particleheattransfercoefficientsinfluidizedbedsbyfrequencyresponsetechniques[C].London:BritishChemicalEngineering,1965,10:260. [16]GUNND.NARAYANANP.Particle-fluidheattransferanddispersioninfluidizedbeds[J].ChemicalEngineeringScience,1981,36:1985-1995. [17]BELMILOUDIA.Heattransfer-mathematicalmodeling,numericalmethodsandinformationtechnology[M].Vienna:InTechVienna,2011:383-408. [18]YANGWJ,ZHOUZY,YUAB.Particlescalestudiesofheattransferinamovingbed[J].PowderTechnology,2015,281:99-111. [19]HOUQ,GANJ,ZHOUZ,etal.Chapterfour-particlescalestudyofheattransferinpackedandfluidizedbeds[J].AdvancesinChemicalEngineering,2015,46:193-243. [20]ZABRODSKYS.Heattransferbetweensolidparticlesandagasinanon-uniformlyaggregatedfluidizedbed[J].InternationalJournalofHeatandMassTransfer,1963,6:23-31. [21]PFEFFERR.HAPPELJ.AnanalyticalstudyofheatandmasstransferinmultiparticlesystemsatlowReynoldsnumbers[J].AIChEJournal,1964,10(5):605. [22]WANGZL,DINGYL,GHADIRIM.Flowofagas-solidtwo-phasemixturethroughapackedbed[J].ChemicalEngineeringScience,2004,59(15):3071-3079. [23]BOYCECM,RICENP,DAVIDSONJF,etal.Magneticresonanceimagingofgasdynamicsinthefreeboardoffixedbedsandbubblingfluidizedbeds[J].ChemicalEngineeringScience,2016,147:13-20. [24]BOYCECM,RICENP,OZELA,etal.Magneticresonancecharacterizationofcoupledgasandparticledynamicsinabubblingfluidizedbed[J].PhysicalReviewFluids,2016,1(7):74-201. [25]GER,YEJ,WANGH,etal.Investigationofgas-solidsflowcharacteristicsinaconicalfluidizedbeddryerbypressurefluctuationandelectricalcapacitancetomography[J].DryingTechnology,2016,34(11):1359-1372. [26]SUTKARVS,DEENNG,SALIKOVV,etal.Experimentalandnumericalinvestigationsofapseudo-2Dspoutfluidizedbedwithdraftplates[J].PowderTechnology,2015,270:537-547. [27] 郭慕孙,李洪钟.流态化手册[M].北京:化学工业出版社,2008:328-359. [28] 金涌.流态化工程原理[M].北京:清华大学出版社,2001:294-332. [29] 李佑楚.流态化过程工程导论[M].北京:科学出版社,2008:68-87. [30]ZHOUZY,YUAB,ZULLIP.Particlescalestudyofheattransferinpackedandbubblingfluidizedbeds[J].AIChEJournal,2009,55(4):868-884. [31]KATOK.Gas-particalheattransferinpackedfluidizedbed[J].JournalofChemicalEngineeringofJapan,1979,12:403-405. [32]GUNND.Transferofheatormasstoparticlesinfixedandfluidizedbeds[J].InternationalJournalofHeatandMassTransfer,1978,21:467-476. [33]WAKAON.KAGUCIS.Effectoffluiddispersioncoefficientsonparticle-to-fluidheattransfercoefficientsinpackedbeds[J].ChemicalEngineeringScience,1979,34:325-336. [34]GELPERINNI,EINSTEINVG.Heattransferinfluidizedbeds[M].London:AcademicPress,1971:471-568. [35] 郭雪岩,柴辉生,晁东海.大颗粒流化床传热数值模拟与气固传热模型比较[J].上海理工大学学报,2012(1):81-87.

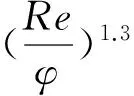
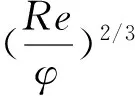
4 结束语
