基于模糊粗糙集和SVM的航空发动机故障诊断*

2017-03-15曹愈远李艳军张丽娜

振动、测试与诊断 2017年1期

关键词：约简粗糙集故障诊断

曹愈远，张建，李艳军，张丽娜

(南京航空航天大学民航学院南京， 211106)

基于模糊粗糙集和SVM的航空发动机故障诊断*

曹愈远，张建，李艳军，张丽娜

(南京航空航天大学民航学院南京， 211106)

随着航空产业的发展，航空发动机故障诊断逐渐向智能化、精确化方向发展，针对这一趋势结合模糊聚类、粗糙集以及支持向量机理论，提出了一种航空发动机故障诊断方法。首先，运用模糊C-均值聚类算法将连续数据离散化；然后，运用粗糙集的知识发现理论，在保持决策表的决策属性和条件属性之间的依赖关系不发生变化的前提下对决策表进行约简；最后，利用支持向量机适用于小样本数据处理的特性对样本进行学习得到最优超平面决策函数从而进行故障诊断。对航空发动机性能参数实例的验证结果表明，该方法对航空发动机故障具有较强的诊断能力，在不影响诊断率的基础上大大缩短了运算时间。因此，提出的算法具有较好的实用性和准确性。

航空发动机；故障诊断；模糊聚类；粗糙集；支持向量机

引言

航空发动机结构复杂、价格昂贵、工作环境恶劣且可靠性难以保证，为故障多发部件，是影响飞行安全的重要因素，对其进行健康监测具有非常重要的意义[1]。传统的故障诊断方法是将发动机监测数据与按照标准模型计算得到的数据进行比较，根据差的大小和决策规则判别发动机是否有故障[2]。

由于航空发动机的复杂性，神经网络等常见方法在实际运用中存在一定的不足，如神经网络存在网络结构选择、容易陷入局部极值、专家系统存在知识不完整和适应性差等问题。依据统计学理论建立而备受关注的支持向量机[3](support vector machines ，简称SVM)可以解决小样本、非线性问题，具有很高的推广性。

虽然支持向量机能解决高维问题，但是随着维数的增加，其计算速度将降低，对计算机的要求变高。航空发动机性能监测参数很多，将所有参数作为输入将是庞大的数据量，实现较为困难，因此提出用粗糙集方法对性能参数进行关键参数提取，但是粗糙集只能处理离散数据，目前离散化方法较多,如等距离划分算法和等频率划分算法等,这些算法使用起来较繁琐。模糊集理论对于模糊、不确定问题具有较好的处理能力,适合进行连续属性值的离散处理。因此笔者采用模糊聚类算法先对原始数据先进行离散化预处理。

1 理论简介

1.1 总体介绍

笔者提出的基于模糊粗糙集和支持向量机的航空发动机故障诊断流程如图1所示。首先，利用模糊聚类方法对性能参数数据进行分类和离散；然后，采用粗糙集算法进行特征参数约简，提取关键参数[4]；最后,用支持向量机算法通过训练学习得到分类模型然后进行故障诊断。

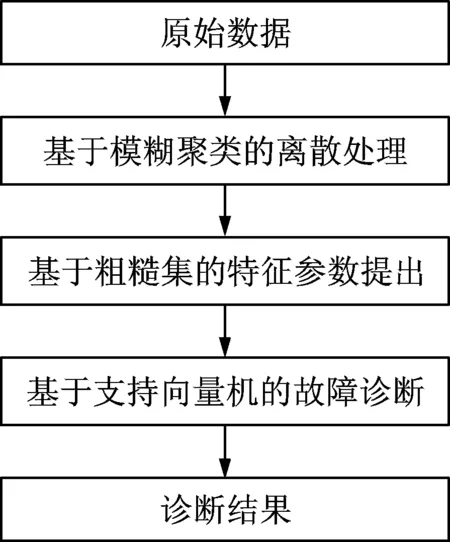
图1 基于模糊粗糙集和支持向量机故障诊断流程Fig.1 The fault diagnosis process based on fuzzy rough set and SVM

1.2 模糊聚类

模糊聚类概念是由Ruspini于1969年首次提出的[5]，系统论述了模糊聚类算法,也有学者相继提出了基于相似关系和模糊关系的聚类方法，目前应用最广泛的是基于目标函数的聚类方法。该方法具有应用范围广和设计简单等优点，本质上可归结为优化问题[6]。基于目标函数的模糊聚类方法的典型代表是由Dunn于1974年首次提出的模糊 C-均值算法(fuzzy c-means algorithm，简称FCMA或FCM)。Bezdek又对该方法进行扩展，建立了较为完善的模糊聚类理论。

1.3 粗糙集

粗糙集(rough set, 简称RS)理论是由Pawlak[7]提出的一种用于处理不完整不精确知识的数学方法。该方法不要求任何先验知识,能有效分析和处理各种不完备数据,并发现其中隐含的信息，揭示其潜在的规律。该理论具有很强的实用性,近年来日益受到重视,方法日趋成熟,在很多领域产生了一些令人关注的应用。Wang等[8]通过对粗糙集的研究,成功开发了一个从历史诊断记录中提取最简规则，并能够对可能发生的故障进行优先级排序的故障分级系统。文献[9]对基于粗糙集的属性约简方法做了研究。

1.4 支持向量机

支持向量机是建立在统计学习理论VC维理论和结构风险最小化原理基础上的机器学习方法[10]，具有坚实的理论基础。简单明了的数学模型在处理小样本、非线性和高维模式识别问题时显示出特有的优势，且在很大程度上克服了“过学习”和“维数灾难”等影响算法性能的关键问题。因此，在模式识别、回归分析、函数估计和时间序列预测等领域都得到了较好的发展[11]。在故障诊断运用方面，万书亭等[12]将SVM 用于滚动轴承故障诊断。曹冲锋等[13]用改进的SVM模型进行旋转机械故障的诊断。沈志熙等[14]提出基于SVM的柴油机故障诊断方法。董明等[15]将SVM用于大型电力变压器的故障诊断。徐启华等[16]将SVM用于航空发动机故障诊断。

2 故障诊断方法

2.1 故障诊断模型

在航空发动机故障诊断模型构建时，性能参数选择的优劣会对发动机故障诊断能力造成重大影响，因此应选择物理意义明确、分辨力强、代表性好的性能参数作为表征航空发动机性能状态的指标。故障诊断模型可表示为以下非线性方程

y=f(X1,X2,…,Xn)

(1)

其中：y为输出值，y=1表示发动机正常工作，y=0表示发动机出现故障；X1,X2,…,Xn为发动机性能状态参数。

假设T=(U,S,C,D)表示一个发动机故障信息系统,其中：U为发动机论域，即故障数据记录的集合；C为连续的条件属性集；D为离散的决策属性集；S=C∪D为属性集[5]。

2.2 基于模糊算法的离散化处理

笔者采用的模糊C-均值聚类算法的步骤[17-18]如下。

1) 初始化：定义模糊加权指数m，聚类类别数C(2≤C≤n，n为样本个数)，迭代停止阈值ε，初始聚类中心P(0)以及迭代次数l，初始状态l=0。

2) 计算划分矩阵U(l):首先，计算表示样本点xk与第i类的聚类中心Pi之间的距离范数dik，其表征样本点与聚类中心的相似度，计算方法为

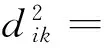
(2)

其中：A为s×s阶的对称正定矩阵，I为单位矩阵；当A=I时，dik为欧氏距离，当A≠I时,dik为马氏距离。

(3)

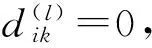
3) 更新聚类中心值

(4)

4) 若‖P(l+1)-P(l)‖<ε，则算法停止；否则转到步骤2。

2.3 基于粗糙集的特征参数提取

基于粗糙集理论的知识发现，其原理是在保持决策表决策属性和条件属性之间的依赖关系不发生变化的前提下对决策表进行约简。假设R表示一族等价关系，如果存在r∈R，使得ind(R)=ind(R-|r|)，则称r为R中不必要的；否则称r为R中必要的。其中：ind(R)表示基于属性R的不可分辨关系。如果每一个r∈R都为R中必要的,则称R为独立的;否则称R为依赖的。若R为独立的,P∈R，则P也是独立的。设Q∈R，若Q为独立的,且ind(Q)=ind(P)，则称Q为P的一个约简。显然，P可以有多个约简[19]。

对离散化的数据进行属性约简,步骤为:a.删除表中相同的规则；b.删除表中多余的条件属性；c.删除分类规则中不必要的属性，简化决策规则；d.利用得到的决策规则进行决策活动。

2.4 基于支持向量机的故障诊断

假设样本集表示为{(xi,yi)}ni=1(其中：输入xi∈Rd，输出yi∈{-1,1})，超平面方程为WTx+b=0,其中：w为可调的权值向量;b为偏值。其优化问题为在满足

yi(WTx+b)≥1 (i=1,2，…,n)

(5)

的约束条件下求

(6)

的最小值。

引入Lagrange乘子法将其转化为对偶问题来解决，即在

；i=1,2，…,n)

(7)

约束条件下求

(8)

的最大值。

(9)

对于非线性不可分模式，通过引入核函数将样本空间映射到高维特征空间，使其线性可分，并在高维特征空间构造最优分类超平面，从而实现分类。引入核函数K(x,y)后的最优分类函数[13]为

(10)

常用的核函数有

多项式核函数K(x,y)=(xTy+1)d

Sigmoid核函数K(x,y)=tanh(β0xTy+β1)

3 实例验证

3.1 诊断模型

以项目组与某航空公司合作获得的某型发动机监测数据为例，选取地面定检加力状态的10组正常数据和10组故障数据为样本数据，选取以下性能参数构建故障诊断模型：低压转子转速N1；高压转子转速N2；进口温度T1；涡轮后燃气温度T4、滑油压力pM、发动机机匣振动值B、风扇进口导向器叶片角度α1、高压压气机可调静子叶片转角α2。样本数据如表1所示，其中:S表示航空发动机状态;1为正常工作;0为出现故障。

表1 性能参数样本

3.2 离散化处理

取性能参数样本点的个数n=20，模糊加权指数m=2，聚类的类别数C=2，迭代停止阈值ε=0.5，初始的聚类中心值P(0)=(0,0,0,0,0,0,0,0)，迭代次数l=50。

3.3 属性约简

约简后的最小决策表如表3所示。这只是诸多最小属性约简中的1种，且约简后的最小决策表中的任何1个属性都不能删除[20]。

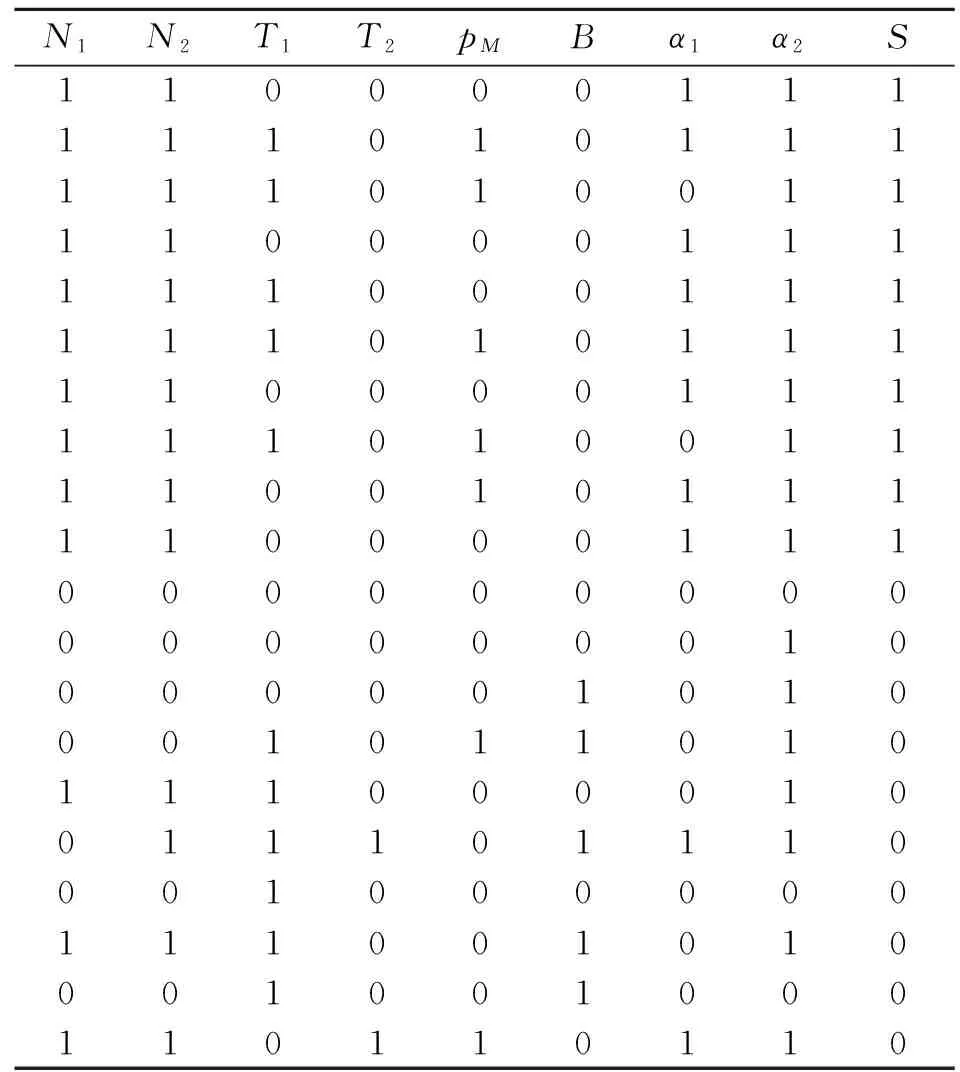
表2 离散化后的决策表

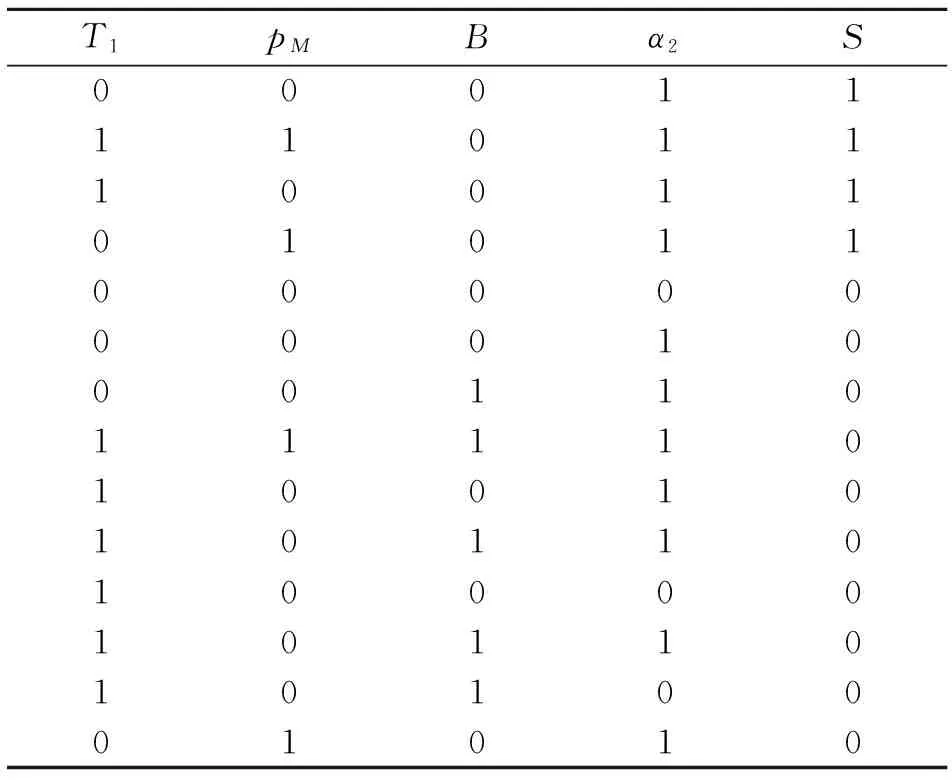
表3 约简后的最小决策表

由约简结果知，原来的8个特征参数利用粗糙集进行约简后只需要4个特征参数即可表征。

3.4 故障诊断

选取地面定检加力状态的100组正常数据和50组故障数据作为样本数据，以60%作为训练样本，40%作为检测样本。以(N1,N2,T1,T2,pM,B,α1,α2)和(T1,pM,B,α2)构建样本空间。

对应的原始值进行归一化处理

(11)

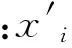
用故障检测率t和误报率f两个指标来衡量诊断的有效性。

故障检测率为

(12)

其中：Ft为故障样本中被检测出的故障个数；Ff为故障样本中被检测出的正常个数。

误报率为

(13)

其中：Tt为正常样本中被检测出的正常个数；Tf为正常样本中被检测出的故障个数。

选取径向基函数作为支持向量机核函数，分别用8个特征向量和约简后的4个特征向量进行向量机训练，运用成熟的支持向量机进行故障诊断结果如表4所示。可以看出：基于模糊粗糙集优化的支持向量机方法能在降低特征参数维数的基础上实现对航空发动机故障的诊断，准确率高达95%，误报率为2.5%，满足适航标准中对航空发动机故障诊断率的要求且计算时间较短，有效提高了计算速度。

表4 航空发动机故障诊断结果

4 结论

1) 基于模糊聚类、粗糙集约简以及支持向量机的特性，提出了一种航空发动机故障诊断方法。

2) 运用模糊C-均值聚类算法将航空发动机连续数据离散化处理，用粗糙集对离散化的数据进行约简，在不影响诊断效果的前提下降低了输入数据的维数，最后用支持向量机对约简后的数据进行故障诊断。

3) 经实例验证，提出的基于模糊粗糙集和支持向量机的航空发动机故障诊断方法能在降低特征参数维数的基础上实现对航空发动机故障的有效诊断。

4) 提出的方法有效降低了运算负载，提高了计算速度，为其他故障诊断方法的简化提供了参考。

[1] 崔建国，严雪，蒲雪萍，等．基于动态PCA与改进SVM的航空发动机故障诊断[J].振动、测试与诊断,2015,35(1):94-99.

Cui Jianguo, Yan Xue, Pu Xuepimg, et al. Aero-engine fault diagnosis based on dynamic PCA and improved SVM[J]. Journal of Vibration, Measurement & Diagnosis, 2015, 35(1):94-99. (in Chinese)

[2] 李凌均,张周锁,何正嘉.支持向量机在机械故障诊断中的应用研究[J].计算机工程与应用,2002,19:19-21.

Li Lingjun, Zhang Zhousuo, He Zhengjia. Application research on support vector machines in mechanical fault diagnosis [J]. Computer Engineering and Applications, 2002, 19:19-21. (in Chinese)

[3] 聂立新，张天侠，赵波. 粒子群算法优化双核支持向量机及应用[J].振动、测试与诊断, 2014,34(3):565-569.Nie Lixin, Zhang Tianxia, Zhao Bo. Dual kernel support vector machine optimized by particle swarm-optimization algorithm and its application[J]. Journal of Vibration, Measurement & Diagnosis, 2014, 34(3):565-569. (in Chinese)

[4] 宋云雪，张传超，史永胜. 基于模糊粗集的航空发动机特征参数提取算法[J] . 航空动力学报, 2008, 23(6): 1127-1130.

Song Yunxue, Zhang Chuanchao, Shi Yongsheng. Extracting algorithm for diagnostic parameters of aero-engine based on fuzzy-rough sets[J]. Journal of Aerospace Power, 2008, 23(6): 1127-1130. (in Chinese)

[5] 陈平, 张钧, 鞠萍华,等.汽轮机故障诊断的粒子群优化加权模糊聚类法[J] . 振动、测试与诊断, 2011, 31(5): 574-576.

Chen Ping, Zhang Jun, Ju Pinghua, et al. Weighted fuzzy clustering method based on particle swarm optimization to fault diagnosis of steam turbine set [J]. Journal of Vibration, Measurement & Diagnosis, 2011, 31(5):574-576. (in Chinese)

[6] 曾山.模糊聚类算法研究[D]. 武汉: 华中科技大学, 2005.

[7] Pawlak Z. Rough sets [J]. International Journal of Information and Computer Sciences, 1982, 11: 341-356.

[8] Wang Qinghui, Li Jingrong. A rough set-based fault ranking prototype system for fault diagnosis [J]. Engineering Applications of Artificial Intelligence, 2004, 17(8): 909-917.

[9] 杨传健，葛浩，汪志圣.基于粗糙集的属性约简方法研究综述[J].计算机应用研究,2012,29(1):16-20.

Yang Chuanjian, Ge Hao, Wang Zhisheng. Overview of attribute reduction based on rough set [J]. Application Research of Computers,2012,29(1):16-20. (in Chinese)

[10]Cortes C, Vapnik V. Support vector networks [J]. Machines Learning, 1995, 20:273-295.

[11]王国胜.支持向量机理论与算法研究[D]. 北京:北京邮电大学, 2005.

[12]万书亭，佟海侠，董炳辉. 基于最小二乘支持向量机滚动轴承故障诊断[J].振动、测试与诊断, 2010, 30 (2):149-152.

Wan Shuting, Tong Haixia, Dong Binghui. Bearing fault diagnosis using wavelet packet transform and least square support vector machines [J]. Journal of Vibration, Measurement & Diagnosis, 2010, 30(2):149-152. (in Chinese)

[13]曹冲锋, 杨世锡, 周晓峰．改进支持向量机模型的旋转机械故障诊断方法[J].振动、测试与诊断, 2009, 29(3):260-269.

Cao Chongfeng, Yang Shixi, Zhou Xiaofeng. Fault diagnosis of rotating machinery based on an improved support vector machines model [J]. Journal of Vibration, Measurement & Diagnosis, 2009, 29(3):260-269. (in Chinese)

[14]沈志熙, 黄席樾, 马笑潇．基于EMD和支持向量机的柴油机故障诊断[J].振动、测试与诊断, 2010,30(1):19-22.

Shen Zhixi, Huang Xiyue, Ma Xiaoxiao．Fault diagnosis of diesel engine based on empirical mode decomposition and support vector machine [J]. Journal of Vibration, Measurement & Diagnosis, 2010,30(1):19-22. (in Chinese)

[15]董明，孟源源，徐长响，等．基于支持向量机及油中溶解气体分析的大型电力变压器故障诊断模型研究[J]．中国电机工程学报,2003,23(7):88-92.

Dong Ming, Meng Yuanyuan, Xu Changxiang, et al. Fault diagnosis model for power transformer based on support vector machine and dissolved gas analysis [J]. Proceedings of the CSEE, 2003, 23(7):88-92. (in Chinese)

[16]徐启华，师军.基于支持向量机的航空发动机故障诊断[J]．航空动力学报，2005,20(2):298-302.

Xu Qihua, Shi Jun. Aero-engine fault diagnosis based on support vector machine[J].Journal of Aerospace Power,2005,20(2):298-302. (in Chinese)

[17]叶海军.模糊聚类分析技术及其应用研究[D]. 合肥:合肥工业大学, 2006.

[18]Bezdek J C. A convergence theorem for the fuzzy ISODATA clustering algorithm[J]．IEEE Transcations of PAMI, 1980,2(1):1-8.

[19]周瑞,杨建国.基于粗糙集与支持向量机的发动机故障诊断研究[J]．内燃机学报，2006,24(4): 379-383.

Zhou Rui, Yang Jianguo. The research of engine fault diagnosis based on rough sets and support vector machine [J].Transactions of CSICE, 2006, 24(4):379-383. (in Chinese)

[20]王广，李军. 基于粗糙集理论的航空发动机故障诊断[J]．航空发动机，2005,31(4):51-53.

Wang Guang, Li Jun. Aeroengine fault diagnosis based on rough sets theory [J]. Aeroengine, 2005, 31(4): 51-53. (in Chinese)