基于参数化时频分析的转子全工况动平衡方法*

2017-03-15周建平温广瑞

振动、测试与诊断 2017年1期

关键词：动平衡稳态幅值

黄鑫, 周建平, 温广瑞,2, 姜宏, 谭媛

(1.新疆大学机械工程学院乌鲁木齐，830047)(2.西安交通大学机械结构强度与振动国家重点实验室西安，710049)

基于参数化时频分析的转子全工况动平衡方法*

黄鑫1, 周建平1, 温广瑞1,2, 姜宏1, 谭媛1

(1.新疆大学机械工程学院乌鲁木齐，830047)(2.西安交通大学机械结构强度与振动国家重点实验室西安，710049)

针对现有转子动平衡方法处理非平稳数据的不足，提出了基于参数化时频分析的转子全工况动平衡方法。该方法根据转频信号频率变化函数构造匹配的旋转算子，将启车信号的时频特征进行旋转，准确提取出转频分量。通过添加试重，结合全息动平衡方法获得各个转速下的迁移矩阵，实现转子全工况的动平衡，避免了传统动平衡方法需要获取稳态数据的缺点。实验结果表明，该方法可以方便、快捷地确定出转子的失衡量和失衡方位,有效降低转子系统不平衡振动，同时减少平衡过程中的启车次数。

参数化时频分析；转子；启车信号；全工况动平衡

引言

转子是旋转机械的核心部件，其振动问题不可避免，转子失衡是旋转机械最常见的故障，消除或者减小转子系统的振动首先应考虑对转子进行动平衡。目前，常用的动平衡方法包括影响系数法[1]和模态平衡法[2]。影响系数法基于线性振动理论，利用不平衡矢量和振动矢量的线性关系计算出校正质量。模态平衡法则是根据转子振型正交原理进行平衡，转子各阶振型的振动只能由相应的振型不平衡所引起，若要降低转子系统振动，须对各阶振型不平衡分别进行校正。影响系数法和模态平衡法都是以转子的稳态响应为基础，即借助转子系统在某些选定转速下的稳态响应数据，通过平衡转速下试重前、后的稳态响应来确定校正质量[3]。现场平衡时，需要进行多次试车才能确定校正质量,平衡效率较低，难以保证在其他转速下有较小的振动。若能通过转子启车阶段的瞬态响应数据快速实现转子的动平衡，降低转子所经历各转速下的振动，将有非常重要的意义[4]。转子的启车信号包含转频分量，倍频分量和分倍频分量。其中，转频分量的振动主要与转子不平衡有关，能否准确提取转子启车过程中转频分量的幅值和相位，对转子动平衡至关重要。

转子的启车信号为典型的非平稳信号，为有效研究这些非平稳信号，时频分析得到了广泛关注。其基本思想是通过将一维时域信号映射到二维时频面，构造时间和频率的联合函数，用它同时描述信号在不同时间和频率的能量密度和强度[5]。常见的时频分析方法主要有短时傅里叶变换(short-time Fourier transform，简称STFT)、小波变换、Wigner-Ville分布和经验模态分解(empirical mode decomposition，简称EMD)。这些方法在分析非平稳信号时具有以下局限性：a.STFT的时频分辨率只与窗函数有关，窗口大小和形状不能随着信号的频率改变而改变，缺乏自适应性；b.小波变换受测不准原理的制约，不能在时域和频域同时达到较高的分辨率，小波基一旦选定，在整个信号分析过程中无法改变；c.Wigner-Ville 分布分析多分量信号时会受到严重的交叉项干扰；d.EMD具有端点效应、模式混叠等问题。以上时频分析方法均没有先验地假定信号的模型，均在不同程度上假设待分析信号为拟平稳信号，故称之为非参数时频方法。

杨扬[6]提出了一种新的分析非平稳信号的方法:参数化时频分析，其本质思想是通过构造与信号匹配的变换核来对其进行时频域旋转，从而使信号时频表示的集中性达到最优。笔者基于参数化时频分析，从启车振动信号中分解出转频振动信号，结合全息动平衡方法[7]实现了转子全工况下的平衡。

1 转子启车过程转频分量提取

1.1 参数化时频分析基本理论

转子的启车信号为调频调幅的多分量信号

(1)

其中:An(t)，fn(t)和αn(t)分别为第n个信号分量的幅值、频率、相位，它们都是随时间变化的函数，利用键相信号可以拟合出转频分量的频率变化函数f(t)。

针对启车信号，结合转频信号频率变化函数f(t)构造匹配的旋转算子为

(2)

将原信号旋转后得到它的一个旋转域为

(3)

式(3)为参数化旋转时频变换。旋转算子ΦR(t)的作用是在时频表示中，将时频特征旋转为一固定频率，把时频旋转后的信号通过带通滤波器，将启车过程转频分量提取出来，具体分解步骤如下。

1) 结合转频信号频率变化函数f(t)构造旋转算子ΦR(t)，图1(a)和图2(a)分别为原始启车信号z(t)时域图和时频谱图。

2) 对原始启车信号进行旋转

Rz(t)=z(t)ΦR(t)

(4)

图1(b)和图2(b)分别为旋转后信号Rz(t)时域图和时频谱图。由图2(b)可知，旋转后的转频分量时频特征与时间轴完全平行，且始终为该分量的初始频率f(0)。

3) 以f(0)为中心频率设计零相移带通滤波器,对旋转信号Rz(t)进行滤波后得到滤波信号Rs(t)。图1(c)和图2(c)分别为滤波信号Rs(t)时域图和时频谱图。

4) 采用旋转算子ΦR(t)对滤波信号Rs(t)进行逆旋转

s(t)=Rs(t)/ΦR(t)

(5)

从而提取出转频分量s(t)。图1(d)和图2(d)分别为转频分量s(t)时域图和时频谱图。

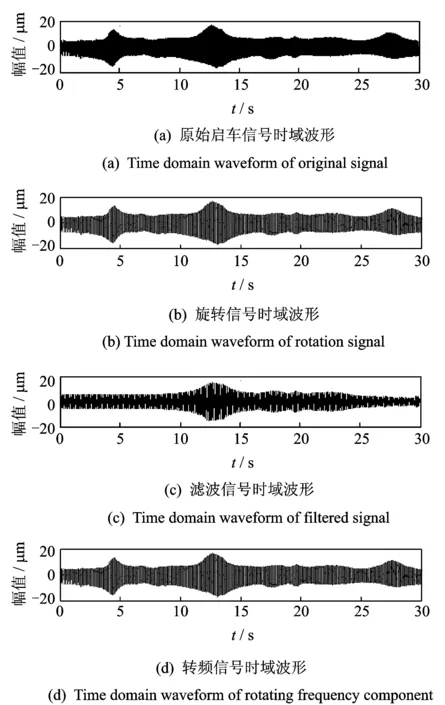
图1 转频分量提取时域波形Fig.1 Time domain waveform of extract rotating frequency component

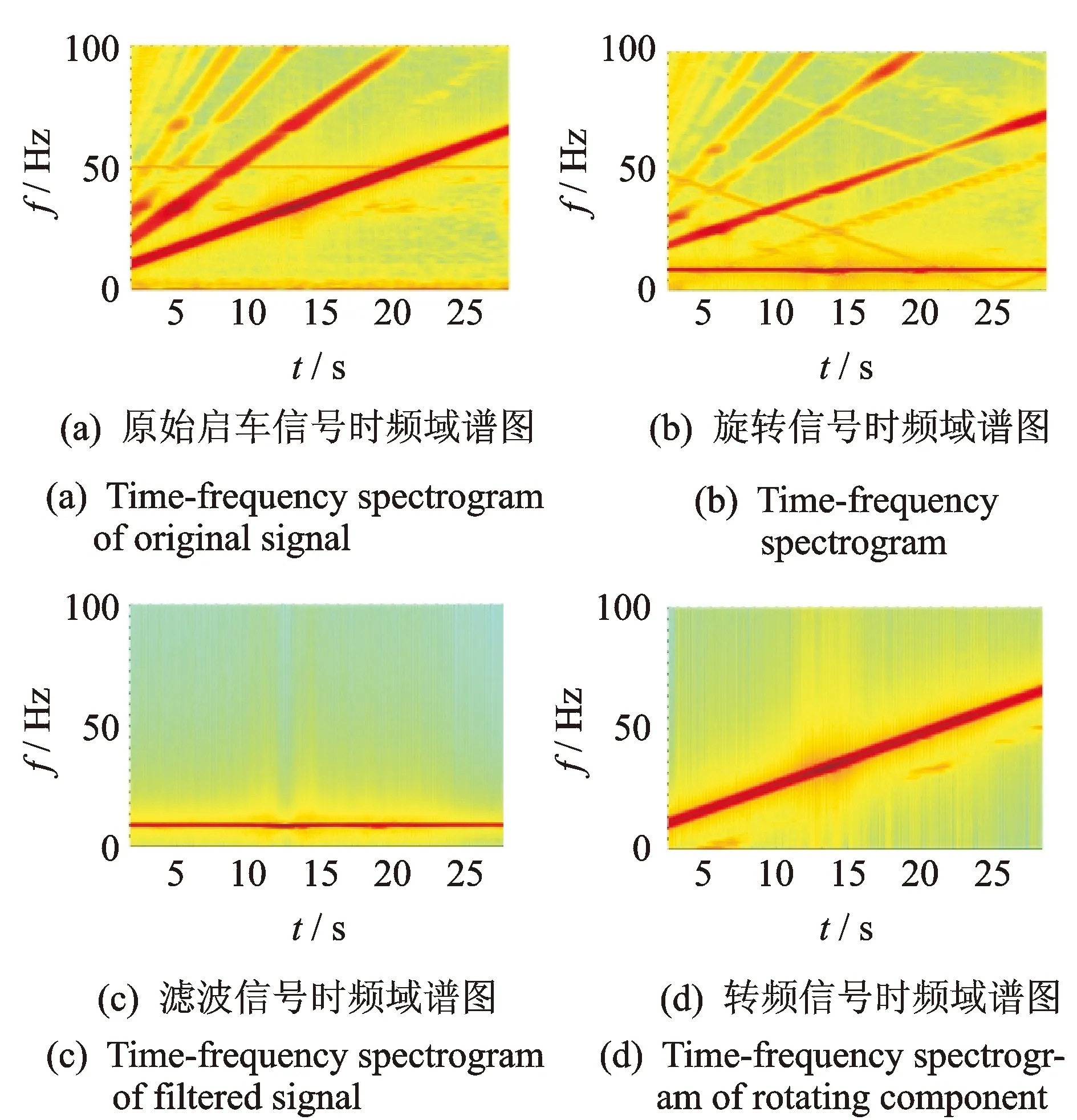
图2 转频分量提取时频域谱图Fig.2 Time-frequency spectrogram of extract rotating frequency component

1.2 转频分量Bode图的绘制

Bode图是常用的分析转子启车信息的方法，可直观显示出启车过程中转子振动的幅值和相位随转速的变化。传统的Bode图绘制方法是间断采样的方法，升速的过程中采集到多组数据,最后通过连接各个数据点得到Bode图，这样做出的Bode图会有不同程度的失真[8]。笔者采用求振动信号复包络的方法绘制转子转频分量的Bode图，既减少了信号采集的次数，又能保证所绘制Bode图的准确性。

参数化时频分析提取的启车过程转频分量[9]为

(6)

对式(6)进行恒等式变换，可得

(7)

其中

(8)

称为转频分量的复包络。

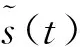
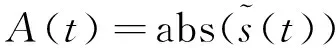
(9)

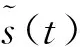
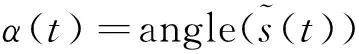
(10)

得到转频分量的幅值和相位之后，就可以准确地绘制出转频分量的启车Bode图。

2 仿真信号分析与实验验证

2.1 仿真信号分析

为验证参数化时频方法提取转频分量的准确性，笔者分别进行了仿真信号分析和实验台验证。仿真信号采用Jeffcott模型，其数学表达式[10]为

该电厂仅有1台619 MWe沸水堆机组，于1964年启动建设，1969年5月实现首次临界，同年9月首次并网发电，12月投入商业运行。在49年的运行期间，该机组总计发电200 TWh，实现超过1.4亿吨的碳减排。

y=Acos(ωt+α)

(11)

其中：A为转子振幅；ω为转子角速度；α为相位。

A，ω，α和转子固有频率的关系为

(12)

其中：e为偏心距；ωn为转子固有频率；cn为阻尼系数。

(13)

仿真启车信号如图3(a)所示，包含转频分量、2倍频分量、3倍频分量、4倍频分量及0.5倍频分量，并添加了SNR=10的噪声信号，采用参数化时频分析的方法从仿真启车信号中提取出转频分量，提取结果和理论转频分量如图3(b)所示。

虽然参数化时频分析提取的转频分量与理论转频分量的吻合程度可以通过波形图直观看出，但还需对提取结果的精度给出定量的评价，笔者选用均方根误差作为评价指标。

(14)

其中：Si为参数化时频分析提取的转频分量的离散值；Xi为理论转频分量离散值；n为离散点数。

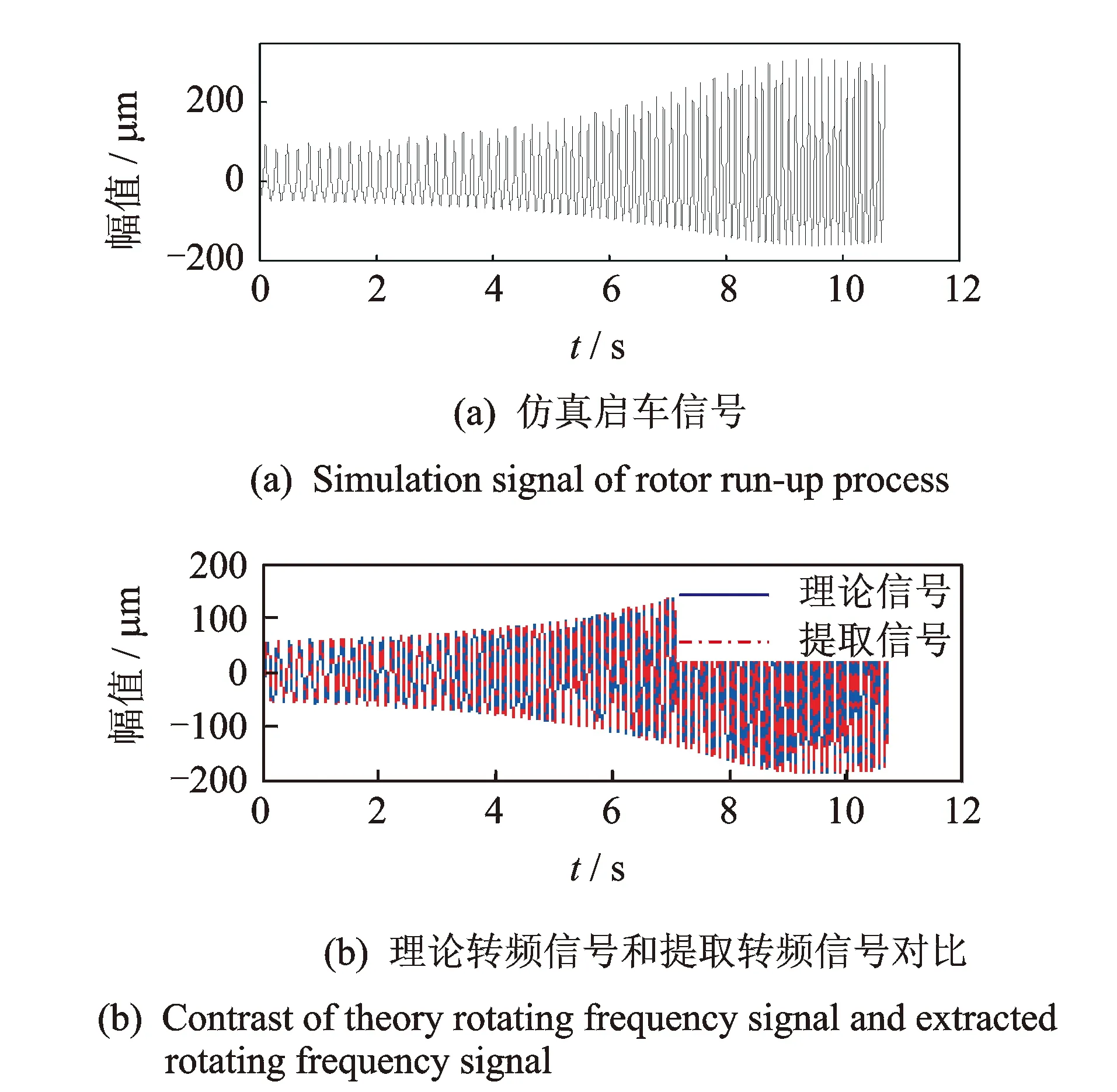
图3 仿真信号分析Fig.3 Simulation signal analysis

2.2 稳态启车实验

笔者在Bently RK4转子实验台上进行实验验证。为了充分考虑转子支撑各向异性的影响，分别在A，B两测量面上安装相互垂直的电涡流传感器，实验台结构和传感器的安装方式如图4所示。

图4 传感器安装示意图Fig.4 The arrangement of sensors

首先，通过转子实验台在转速范围为600～3 100 r/min之间每隔20 r/min采集一组稳态振动数据，采样频率为2 048 Hz，采样点数为2 048。将采集到的126组稳态启车振动数据通过快速傅里叶变换求得转频分量的幅值和相位，并采用频谱校正方法对转频幅值和相位进行校正,计算出较为精确的转频幅值和相位值。然后，通过转子实验台采集转速范围为600～3 100 r/min之间的连续启车数据，采样频率为2 048 Hz，用参数化时频方法提取转频分量，根据其复包络求出转频分量的幅值和相位。图5为4个通道的稳态启车和连续启车幅值相位对比图。

选用式(14)均方根误差作为评价指标，Si为连续启车转频分量的离散值，Xi为稳态启车转频分量离散值。各通道均方根误差如表1所示。

仿真信号分析及稳态启车实验表明，参数化时频分析方法能够准确地提取出转子启车过程转频分量，具有良好的精度及可靠性。

表1 连续启车与稳态启车转频分量均方根误差

Tab.1 RMSE of steady start signal and continuously start signal

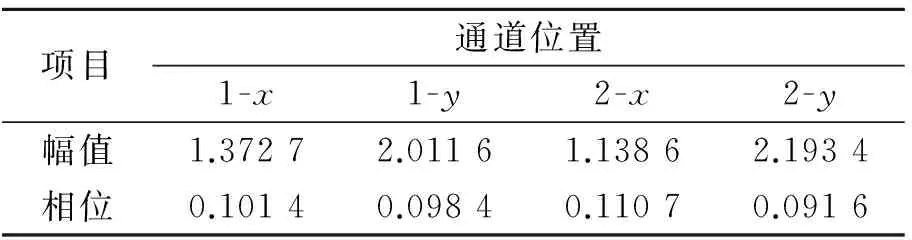
项目通道位置1-x1-y2-x2-y幅值1.37272.01161.13862.1934相位0.10140.09840.11070.0916

3 动平衡实验

在Bently RK4转子实验台上进行动平衡实验，设置采样频率为2 048 Hz，测量得到转子系统在600～3 100 r/min范围内的启车振动信号。利用参数化时频方法提取出转频分量，根据其复包络求出转频分量的幅值和相位，如图6所示。

在转子实验台A校正平面添加0.6g<135°的试重，在转子实验台B校正平面添加0.6g<225°的试重，保持采样参数和升速比不变，再次测量A，B两截面的启车振动信号，利用参数化时频方法提取出转频分量，求出转频分量的幅值和相位。

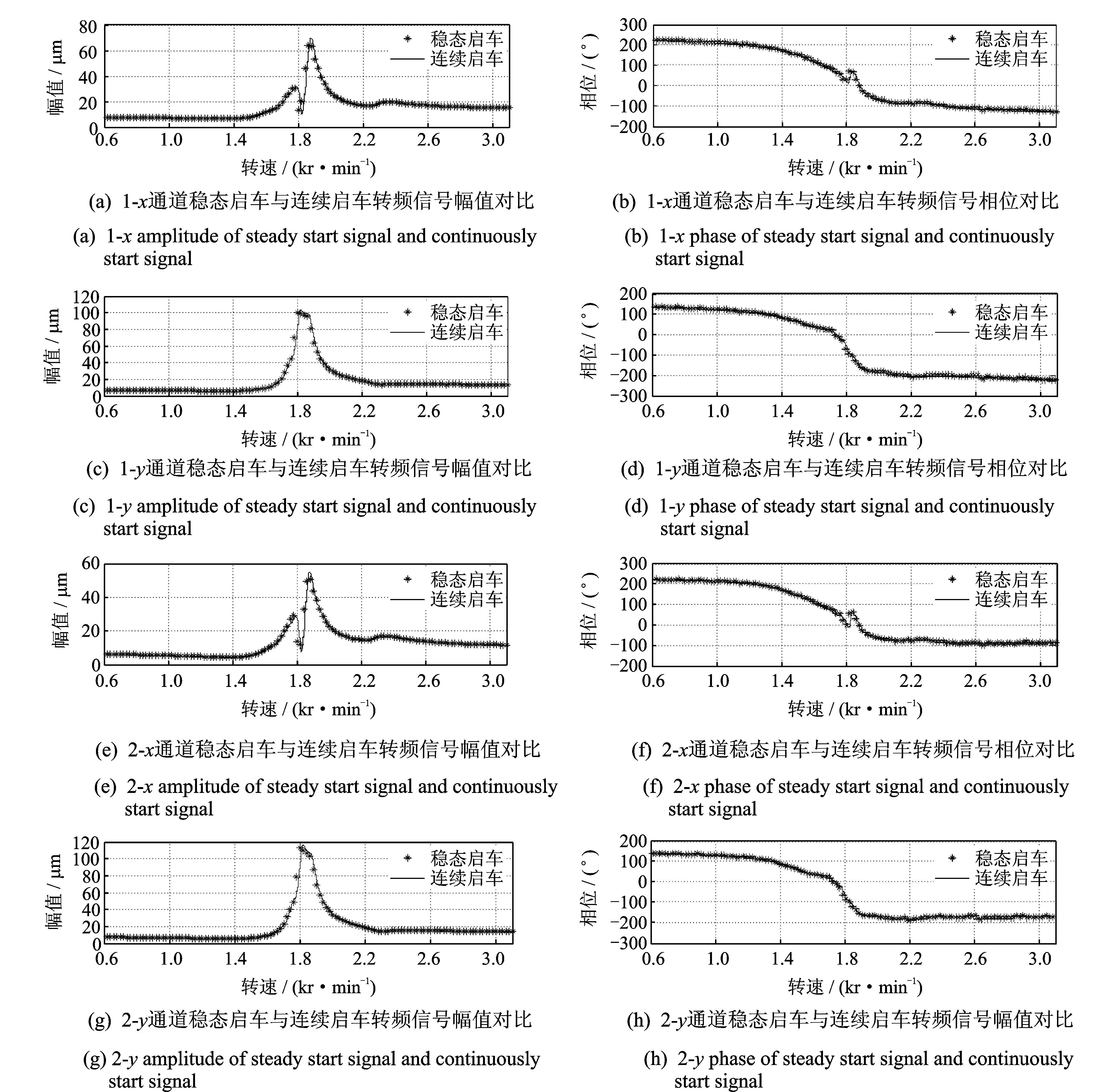
图5 4个通道稳态启车与连续启车转频信号对比Fig.5 Contrast of steady start signal and continuously start signal

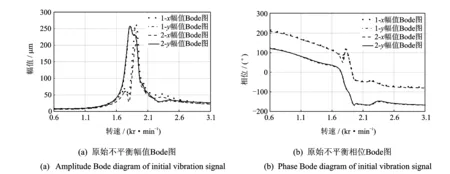
图6 原始不平衡幅值和相位Bode图Fig.6 Amplitude and phase bode diagram of initial vibration signal

由原始启车振动信息和加试重后启车振动信息可以求得转子在600～3 100 r/min范围内每一个转速下的迁移矩阵，即转子全工况下的迁移矩阵。结合全息动平衡方法可以实行转子全工况的动平衡。

为验证上述全工况动平衡方法，笔者分别选择1 650 r/min和2 000 r/min处的振动信息进行动平衡计算，分析其对临界转速处振动和工作转速处振动的平衡效果，选取3 000 r/min作为转子的工作转速。选取1 650 r/min处的振动信息进行全息动平衡，配重计算数据如表2所示。

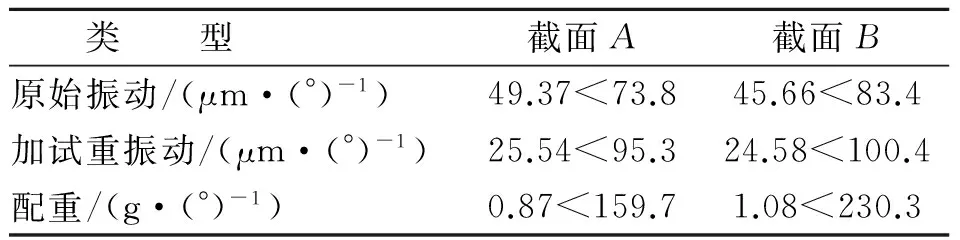
表2 1 650 r/min配重计算数据表

选取2 000 r/min处的振动信息进行全息动平衡，配重计算数据如表3所示。

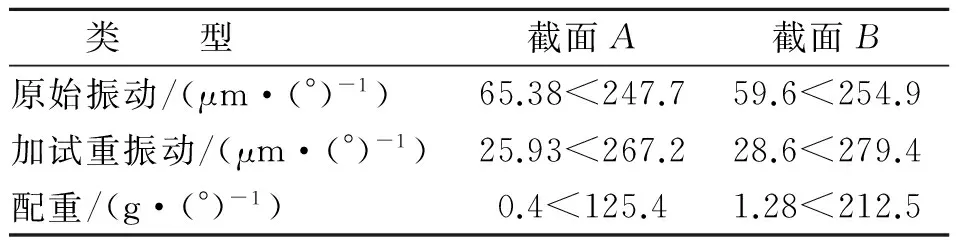
表3 2 000 r/min配重计算数据表

选取1 650 r/min处的振动信息进行全息动平衡时，实际加重A面0.9 g<157.5°，B面1.1g<225°，平衡前后临界转速处振动幅值与工作转速处振动幅值如表4所示。选取2 000 r/min处的振动信息进行全息动平衡时，实际加重A面0.4 g<135°，B面1.3 g<225°，平衡前后临界转速处振动幅值与工作转速处振动幅值如表5所示。图7为4个通道平衡前后振动幅值的对比。由实验结果可知，1 650 r/min处和2 000 r/min处的振动信息均可以有效降低临界转速处和工作转速处的振动幅值。

表4 1 650 r/min平衡效果

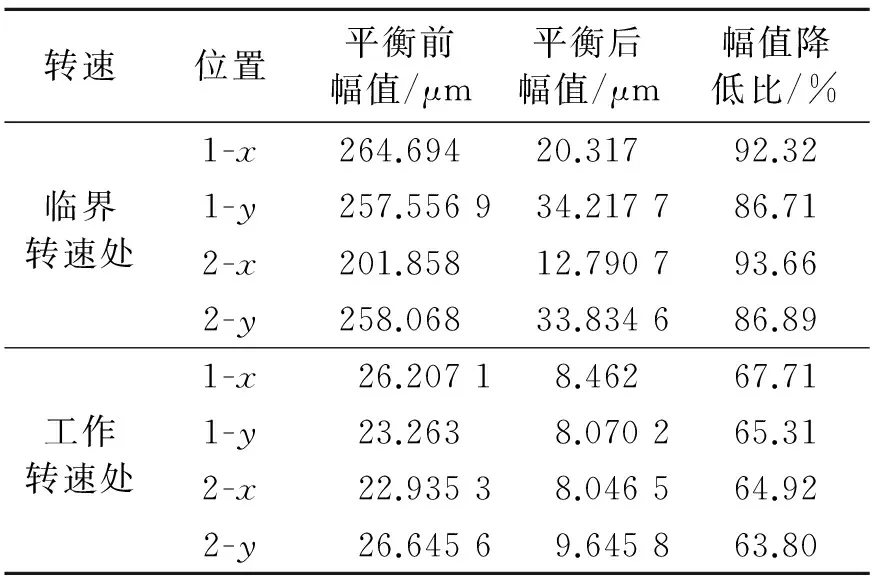
表5 2 000 r/min平衡效果

4 结束语

采用参数化时频方法准确地提取出了转子启车信号中的转频分量，并进行仿真信号分析和实验验证。提出了基于转子启车信号的全工况动平衡方法，可以有效降低临界转速处和工作转速处的振动，并进行了实验验证。提出的动平衡方法和传统平衡方法相比有以下优点：a.采集信号方便，只需要采集转子启车过程中的振动数据，不需要采集某一转速下的稳态数据；b.启车次数少，该方法只需转子的两次加速启动过程即可获得转子全工况下的迁移矩阵，从而实现对转子的平衡；c.平衡效果好，可以有效降低转子工作转速和临界转速下的振动。

[1] Goodman T P. A least-squares method for computing balance corrections[J]. Transaction of ASME，Journal of Engineering for Industry, 1964, 86(3): 273-279.

[2] Bishop R E D, Parkinson A G. On the isolation of modes in balancing of flexible shafts[J]. Proceedings of the Institution of Mechanical Engineers, 1963, 177(16): 407-426.

[3] 温广瑞, 臧廷朋, 廖与禾. 基于非平稳信息的转子瞬态动平衡方法[J]. 振动、测试与诊断, 2013, 33(4): 614-619.

Wen Guangrui, Zang Tingpeng, Liao Yuhe. Transient balancing of rotor based on non-stationary information[J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(4): 614-619. (in Chinese)

[4] Huang Jinping. Two-plane balancing of flexible rotor based on accelerating unbalancing response data[J]. Acta Aeronautica Et Astronautica Sinica, 2010, 31(2): 400-409.

[5] Flandrin P. Time-frequency/time-scale analysis[M]. San Diego: Academic Press, 1999:43-45.

[6] 杨扬. 参数化时频分析理论、方法及其在工程信号分析中的应用[D]. 上海: 上海交通大学, 2013.

[7] 屈梁生, 邱海, 徐光华. 全息动平衡技术：原理与实践[J]. 中国机械工程, 1998, 9(1): 60-63.

Qu Liangsheng, Qiu Hai, Xu Guanghua. Rotor balancing based on holospectrum analysis:principle and practice[J]. China Mechanical Engineering, 1998, 9(1): 60-63. (in Chinese)

[8] 盖广洪. 基于经验模态分解的转子启动波德图绘制[J]. 机械科学与技术, 2006, 25(1): 9-11.

Gai Guanghong. Bode diagram plotting of rotor start up based on empirical mode decomposition[J]. Mechanical Science and Technology, 2006, 25(1): 9-11. (in Chinese)

[9] Zhang Xining, Guo Jinliang, Wu Jili. A new calculation method for Bode and Nyquist diagrams of rotor startup or shutdown and its application[C]∥ Proceedings of 11th IEEE International Conference on Control & Automation (ICCA). Piscataway, NJ: IEEE, 2014: 377-382.

[10]钟一谔. 转子动力学[M]. 北京: 清华大学出版社, 1987:3-5.