基于地震响应的结构鲁棒性定量分析方法*
2017-03-15杜永峰徐天妮
包 超, 杜永峰, 徐天妮, 祁 磊, 宋 翔
(1.兰州理工大学防震减灾研究所 兰州,730050)(2.兰州理工大学西部土木工程防灾减灾教育部工程研究中心 兰州,730050)(3.宁夏大学土木与水利工程学院 银川,750021)
基于地震响应的结构鲁棒性定量分析方法*
包 超1,3, 杜永峰1,2, 徐天妮1, 祁 磊1, 宋 翔1
(1.兰州理工大学防震减灾研究所 兰州,730050)(2.兰州理工大学西部土木工程防灾减灾教育部工程研究中心 兰州,730050)(3.宁夏大学土木与水利工程学院 银川,750021)
为了研究结构抗连续倒塌鲁棒性,基于地震作用下框架结构受力特征,结合备用荷载路径法与动力时程分析法,提出了结构鲁棒性定量分析方法,并根据震级-震中距条带地震动记录选取方法选取随机地震动记录进行算例分析和验证。研究表明,结构的鲁棒性优劣是一个相对概念,与外部作用强度呈反相关关系;通过定量分析结构鲁棒性,可以在多个结构方案筛选时提供一定的参考;降低重要构件的损伤风险,对易损性系数和重要性系数均较大的构件设置提供可靠保护,加强构件之间相互联系,提高备用荷载路径的可靠性,能够增强结构的鲁棒性。
地震响应; 结构分析; 随机振动; 结构鲁棒性; 构件重要性系数; 构件易损性系数
引 言
结构的鲁棒性用于描述建筑结构承受局部损伤并抵抗不相称破坏的能力[1]。增强结构的鲁棒性,并非意味着需要对结构进行过度设计,而是指在个别承重构件丧失承载力后,剩余结构能够重新分配原本由该失效构件承担的荷载,并防止出现因局部初始失效而造成更大范围的破坏甚至倒塌的情况。
目前,国内外学者针对结构鲁棒性研究做了大量研究。张成等[2]基于H∞理论提出一种采用系统传递函数的结构鲁棒性进行定量评价的方法。Fascetti 等[3]基于静力非线性分析方法和动力非线性分析方法,推导了一种可用于比较钢筋混凝土框架结构抗连续倒塌的相对鲁棒性分析方法。叶列平等[4]提出了以拆除构件对广义结构刚度的影响程度作为该构件重要性评价指标。吕大刚等[5]采用3种不同的鲁棒性指标,对按照我国现行规范设计的钢筋混凝土框架结构的抗震鲁棒性进行了定量评价。Jeyaraja等[6]将各种构件性能用于结构抗连续倒塌鲁棒性分析中,并利用该方法对框架柱突然失效条件下钢混组合框架结构的鲁棒性进行了分析。叶俊等[7]提出H∞结构鲁棒性评价指标,并对弦支结构的鲁棒性展开研究。王伟等[8]提出了一种加固型栓焊盖板连接构造及其设计方法来提高结构抗连续倒塌鲁棒性。
结构鲁棒性研究虽然取得了一定成果,但仍然没有建立一个可以被广泛接受的结构鲁棒性定量评价方法[9]。笔者综合备用荷载路径法与动力时程分析法,提出基于地震响应的结构鲁棒性定量评价方法,探讨了构件重要性、构件易损性和结构鲁棒性与外部激励之间的关系,以及增强结构鲁棒性的方法。
1 结构鲁棒性简化评价方法
与结构竖向连续倒塌类似,结构水平增量连续倒塌往往始于个别框架柱的失效。因此,根据地震作用下框架柱失效而导致结构连续倒塌[6],结合备用荷载路径法和动力时程分析法将底层框架柱失效作为分析工况。
1.1 构件重要性系数
构件重要性系数反映极端条件下个别构件承载力的丧失对原结构承载力的影响程度,确定构件重要性系数是计算结构鲁棒性系数的基础[10]。
高扬[11]提出了基于桁架结构承载力设计基准值的构件重要性系数。黄冀卓等[12]提出了基于特定竖向荷载作用的构件重要性系数计算方法。地震等水平随机作用是影响结构安全的主要因素,因此针对地震动激励与重力荷载耦合作用下底层柱失效对原结构响应的影响程度作为重要性系数的评判指标,即
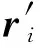
底层框架柱的柱底为固接,在失效前后柱底端产生的位移远小于顶端的位移可忽略不计,底层第柱对结构总能量分布影响可简化为
(3)
1.2 构件易损性系数
现有研究大都针对结构整体易损性展开,而结构易损性通常取决于结构布置形式、建筑材料和构造措施等。黄靓等[13]建立了多种荷载共同作用时的构件易损性定量分析方法。为了避免对各变量变化过于敏感,根据地震作用下结构受力特征对计算方法做了相应改进,即
(4)

1.3 结构鲁棒性系数
构件的重要性系数反映不同构件在抵御结构破坏时所做的贡献,构件易损性系数反映了构件在荷载作用下的易损程度,将二者综合起来对结构鲁棒性做出的评价才更为全面。考虑到文献[11]提出的结构鲁棒性定量评价方法对计算式中各变量太过灵敏而难以对外部影响进行区别,所以在此基础上做了进一步简化
(5)
其中:R,γi和φi依次为结构鲁棒性系数、构件重要性系数和构件易损性系数;n为分析的构件总数。
2 算例分析
2.1 分析模型
根据规范设计了一座典型的五层三跨钢筋混凝土框架结构,以SeismoStruct为平台建立有限元模型。混凝土和钢筋分别选用Mander模型和Menegotto-Pinto模型,梁柱均采用基于力的纤维模型非弹性框架单元infrmFB,底层层高为3.6 m,其余各层层高为3.0 m;框架柱截面为500 mm×500 mm,纵梁和横梁截面分别为550 mm×300 mm和450 mm×250 mm;混凝土和钢筋分别为C30级和HRB400级。结构抗震设防烈度为8度,按Ⅱ类场地考虑地震作用。恒载和活载分别取3.5 kN/m2和2.0 kN/m2。分析模型平面双向对称,为了避免重复计算,取相同结构参数的一部分作为研究对象,模型平面布置及工况分布如图1所示。
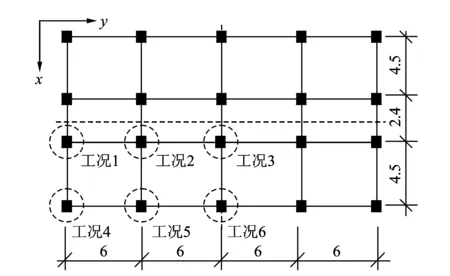
图1 模型平面布置图(单位:m)Fig.1 Plan-view of model(unit: m)
2.2 地震动记录选取
地震动记录有很强的不确定性,而这种不确定性对结构响应造成的影响甚至大于结构自身的不确定性。为了避免地震动记录不确定性对计算结果产生明显的倾向性干扰,通过地震和台站信息对所选地震动记录进行筛选。其中,地震信息主要包括震级和震源机制信息,台站信息主要包括场地特征和震中距等信息,将二者结合可以更直观地进行地震动记录的筛选。因此,笔者按照震级-震中距(Mw-R)条带选波方法[14]选取地震动记录。常用地震动记录可以划分为4个Mw-R条带:小震级小震中距(small magnitude and small distance,简称SMSR,5.8 表1 地震动记录 在进行构件易损性分析时,为了分析地震强度水准与结构鲁棒性之间的关系,分别设定了4个强度水准地震作用进行分析:抗震设防烈度8度时的多遇地震加速度时程最大值为0.07g,基本地震加速度0.2g,罕遇地震加速度时程最大值0.4g,以及超烈度地震加速度峰值,即9度设防烈度时的罕遇地震加速度时程最大值0.62g。各地震激励沿结构x向施加于结构。 3.1 构件重要性系数 图2为16条地震激励下各工况对应构件的重要性系数曲线。散点表示不同强度地震作用下各构件的重要性系数,折线为各散点的平均值曲线。构件重要性系数随着地震动强度的变化而有所不同,但无论地震激励选自哪种震级-震中距条带,其对应的构件重要性系数平均值曲线都表现出了近乎相同的规律,即角柱重要性系数最大,短向边柱重要性系数次之,随后依次是长向边柱和中柱。分析可知,当初始失效发生后,原有的荷载路径被破坏,上部荷载需要通过备用荷载路径分配和传递。与工况4中角柱相连接的框架梁此时类似于悬挑构件,在上部荷载重分布过程中仅可以提供梁机制,而梁机制承载力相对较小,成为影响剩余结构承载力的最薄弱环节,构件重要性系数最大。边柱失效后,与之相连的框架梁可以同时提供梁机制和悬链线机制作为备用荷载路径,剩余结构整体承载力也因此未受太大影响。失去中柱的剩余结构可以利用承载力较高的双向悬链线机制对上部荷载重新分配传递,剩余结构承载能力损失最小,相应构件重要性系数则最大。 除了对剩余结构承载力产生影响外,初始失效构件还会影响剩余结构地震响应,进而影响构件重要性系数。对于平面内双向对称结构,无初始损伤的原结构底层框架的刚心和质心在平面内是相互重合的,但随着初始失效框架柱承载力和刚度的丧失,结构底层平面刚心将会偏离原位,底层原本重合的刚心和质心之间产生了一定距离,导致结构在地震作用下产生扭转效应。在分析的6个工况中,工况1和工况4对应的初始失效框架柱与结构底层平面刚心的距离最大,使得与这两个工况对应的剩余结构地震响应大于其他剩余结构,构件重要系数也更大。 3.2 构件易损性系数 图3为不同Mw-R地震激励下底层各框架柱的易损性系数平均值柱状图。比较发现,在地震动强度较低的时候,某些构件的受损风险却较其他构件要略大,但当地震动强度增大到一定程度时,这些构件损伤风险的增幅却相对较小。以图3(a)为例,在多遇地震作用下,工况1和工况4对应的底层框架柱损伤风险明显低于其余4个框架柱。在设防地震作用下,底层框架柱的损伤风险都有所增加,但各框架柱受损风险的增长幅度却有所区别,工况1和工况4对应的底层框架柱受损风险增幅较大,而其余框架柱的受损风险增幅却较小,这使底层框架柱的受损风险更加接近。当结构遭受罕遇地震时,工况1和工况4对应的框架柱受损风险进一步大幅提高,且明显高于其余构件受损风险,这一特点尤以结构超烈度地震作用下明显。对于这种现象分析可知,多遇和设防地震强度相对较小,在这两种地震动强度作用下,结构的响应基本保持在线性状态内,在相互耦合的各内力中构件的轴力对于其承载能力影响较大,工况1和工况4中框架柱承受的竖向恒载和活载相对较小,则损伤风险也较低,而工况2和工况3对应的中柱承担的竖向荷载最大,损伤风险也最高。当地震动强度增大至罕遇地震和超烈度地震时,结构中除了出现多遇和设防地震时相似的竖向荷载与水平作用力外,还会在大幅度摆动过程中会产生较大的倾覆力矩,距离结构平面刚心较远的框架柱轴力显著增大,导致不同内力对其达到极限承载能力的贡献也产生变化,即轴力对距离结构平面刚心较远的框架柱破坏发挥了重要作用,致使工况4,5,6中构件的受损风险大幅度提高。在这3个工况中,工况4的受损风险增幅最为明显,主要因为在强震作用下大量构件进入非线性状态,该工况对应于角柱,可用的备用荷载路径数量远少于边柱和中柱,荷载无法有效地分散和传递,使其受损风险最大。因此,在进行结构抗震设计时,除了考虑基本的抗震需求,还应该尽量保证备用荷载路径较少的构件的安全性,以免出现强震中这种构件过早失效的现象。 图2 构件重要性系数曲线Fig.2 Member importance coefficient curve of columns 从图3还可以看出,选自不同Mw-R的地震动激励引起各构件的损伤风险也有所不同。震级和震中距条带直接决定了所选地震激励的特性,从而间接影响到结构和构件的地震响应。对于同样高震级的LMSR和LMLR两个条带,从LMSR中选取的地震动记录能够引起较大的构件易损性系数,而LMLR引起的构件易损性系数却相对较小。这是因为同样震级的地震中,当测站的震中距较小时,地震动会表现出一定的近场地震特征,如速度大脉冲、破裂方向性效应等[16]。近场地震动的这些特有属性通常正是导致结构出现较为严重的损伤和破坏的主要原因,因此选自LMSR的地震激励对应于较大的构件易损性系数。与之相类似,低震级两个条带SMSR和SMLR中,SMSR对应于较大的易损性系数。与震中距对构件易损性的间接影响类似,震级也对构件易损性系数的大小产生了一定影响,但小于震中距所产生的影响。 图3 构件易损性系数柱状图Fig.3 Histogram of member vulnerability coefficient 3.3 结构鲁棒性系数 不同Mw-R条带的地震激励下的结构鲁棒性系数曲线如图4所示。可以看出,不同Mw-R条带的地震激励下,结构鲁棒性系数均随着地震强度水准的提高而降低,即结构鲁棒性随着地震强度的增强而变差。此外,结构在不同Mw-R条带地震动激励下鲁棒性有明显差别,但随着地震动水准的不断提高,不同地震激励对结构鲁棒性造成影响的差异也在减小,尤其在及罕遇地震水准时结构鲁棒性系数趋于相同。 图4 结构鲁棒性系数曲线Fig.4 Structural robustness coefficient curve 可见,增加结构冗余度,减轻局部构件失效对原结构的影响程度,同时提高各构件的承载力,降低构件损伤风险,可有效增强结构鲁棒性。 1) 结构鲁棒性的优劣是相对的,取决于结构自身特性、所分析各构件的失效风险和影响程度,以及外部荷载的大小。 2) 结构鲁棒性随着外部荷载强度的提高而降低,震中距远近对结构鲁棒性产生的影响较震级高低更为显著,但在超烈度地震作用下结构鲁棒性趋于一致。 3) 同等水准地震作用下,中柱重要性系数最小,短向边柱和长向边柱次之,角柱最大;各框架柱的构件易损性系数大小相对关系则随地震强度水准的不同而有所不同。合理设计结构形式、增加备用荷载路径和结构冗余度数量、提高备用荷载路径的荷载传递效率,可直接降低构件的损伤风险及其失效对结构的影响,提高结构鲁棒性。 4) 结构鲁棒性定量分析方法处于探索阶段,笔者提出的分析方法可以对结构鲁棒性优劣相对关系做出分析,尚无法给出一个可供参考的绝对标准,还需对结构鲁棒性定量分析方法做进一步研究。 [1] ASCE 7-05. Minimum design loads for buildings and other structure[S]. New York: American Society of Civil Engineers, 2006. [2] 张成,吴慧,高博青,等. 基于H∞理论的结构鲁棒性分析[J]. 建筑结构学报, 2012,33(5):87-92. Zhang Cheng, Wu Hui, Gao Boqing, et al. H∞-based structural robustness analysis[J]. Journal of Building Structures, 2012,33(5):87-92. (in Chinese) [3] Fascetti A, Kunnath S K, Nisticò N. Robustness evaluation of RC frame buildings to progressive collapse[J]. Engineering Structures, 2015,86:242-249. [4] 叶列平,林旭川,曲哲,等.基于广义结构刚度的构件重要性评价方法[J].建筑科学与工程学报, 2010,27(1):1-6, 20. Ye Lieping, Lin Xuchuan, Qu Zhe, et al. Evaluating method of element importance of structural system based on generalized structural stiffness[J]. Journal of Architecture and Civil Engineering, 2010,27(1):1-6,20. (in Chinese) [5] 吕大刚,宋鹏彦,崔双双,等.结构鲁棒性及其评价指标[J].建筑结构学报,2011,32(11):44-54. Lü Dagang, Song Pengyan, Cui Shuangshuang, et al. Structural robustness and its assessment indicators[J]. Journal of Building Structures, 2011,32(11):44-54. (in Chinese) [6] Jeyarajan S, Liew J Y R, Koh C G. Progressive collapse mitigation approaches for steel-concrete composite buildings[J]. International Journal of Steel Structures, 2015,15(1):175-191. [7] 叶俊,高博青,董石麟.基于线性鲁棒性优化的弦支结构设计及分析[J].计算力学学报,2014,31(2):149-154. Ye Jun, Gao Boqing, Dong Shilin. Linear robustness based optimization design of cable supported structure and its performance analysis[J]. Chinese Journal of Computational Mechanics, 2014,31(2):149-154. (in Chinese) [8] 王伟,秦希.基于结构鲁棒性提升的隔板贯通节点加固构造[J].同济大学学报:自然科学版,2015,43(5):685-692. Wang Wei, Qin Xi. Retrofitted connection details of through diaphragm joint for structural robustness enhancement[J]. Journal of Tongji University: Natural Science, 2015,43(5):685-692. (in Chinese) [9] Biondini F, Frangopol D M, Restelli S. On structural robustness, redundancy and static indeterminacy[C]∥Proceedings of the 2008 ASCE-SEI Structures Congress. Vancouver, Canada:[s.n.], 2008:1-5. [10]蔡建国,王蜂岚,韩运龙,等.大跨空间结构重要构件评估实用方法[J].湖南大学学报:自然科学版,2011,38(3):7-11. Cai Jianguo, Wang Fenglan, Han Yunlong, et al. Practical method for the evaluation of important structural components of long-span space structures[J]. Journal of Hunan University: Natural Science Edition, 2011,38(3):7-11. (in Chinese) [11]高扬.结构鲁棒性定量计算中的构件重要性系数[D].上海:上海交通大学, 2009. [12]黄冀卓,王湛.钢框架结构鲁棒性评估方法[J].土木工程学报,2012,45(9):46-54. Huang Jizhuo, Wang Zhan. An approach for evaluation of the structural robustness of steel frames[J]. China Civil Engineering Journal, 2012,45(9):46-54. (in Chinese) [13]黄靓,王蓥,陈永亮,等.一种简化的结构鲁棒性量化方法[J].工程力学,2013,30(10):46-53. Huang Liang, Wang Ying, Chen Yongliang, et al. A simplified evaluation method of structural robustness[J]. Engineering Mechanics, 2013,30(10):46-53. (in Chinese) [14]于晓辉.钢筋混凝土框架结构的概率地震易损性与风险分析[D].哈尔滨:哈尔滨工业大学, 2012. [15]Pacific earthquake engineering research center (PEER). 2008 PEER next generation attenuation(NGA) database[OL]. [2015-06-20]. http:∥peer.berkeley.edu/nga. [16]贾俊峰,杜修力,韩强.近断层地震动特征及其对工程结构影响的研究进展[J].建筑结构学报,2015,36(1):1-12. Jia Junfeng, Du Xiuli, Han Qiang. A state-of-the-art review of near-fault earthquake ground motion characteristics and effects on engineering structures[J]. Journal of Building Structures, 2015,36(1):1-12. (in Chinese) 10.16450/j.cnki.issn.1004-6801.2017.01.019 *国家自然科学基金资助项目(51178211,51578274) 2015-08-03; 2015-10-05 TU375; TH123+.4 包超,男,1986年4月生,博士生。主要研究方向为结构减震控制和工程结构抗震。曾发表《竖向不规则RC框架结构连续倒塌动力放大系数研究》(《四川大学学报: 工程科学版》2015年第47卷第2期)等论文。 E-mail: bc863@foxmail.com 通信作者简介:杜永峰,男,1962年3月生,教授、博士生导师。主要研究方向为结构减震控制、结构随机振动及可靠度分析。 E-mail: doyf@sohu.com
3 结构抗连续倒塌鲁棒性分析
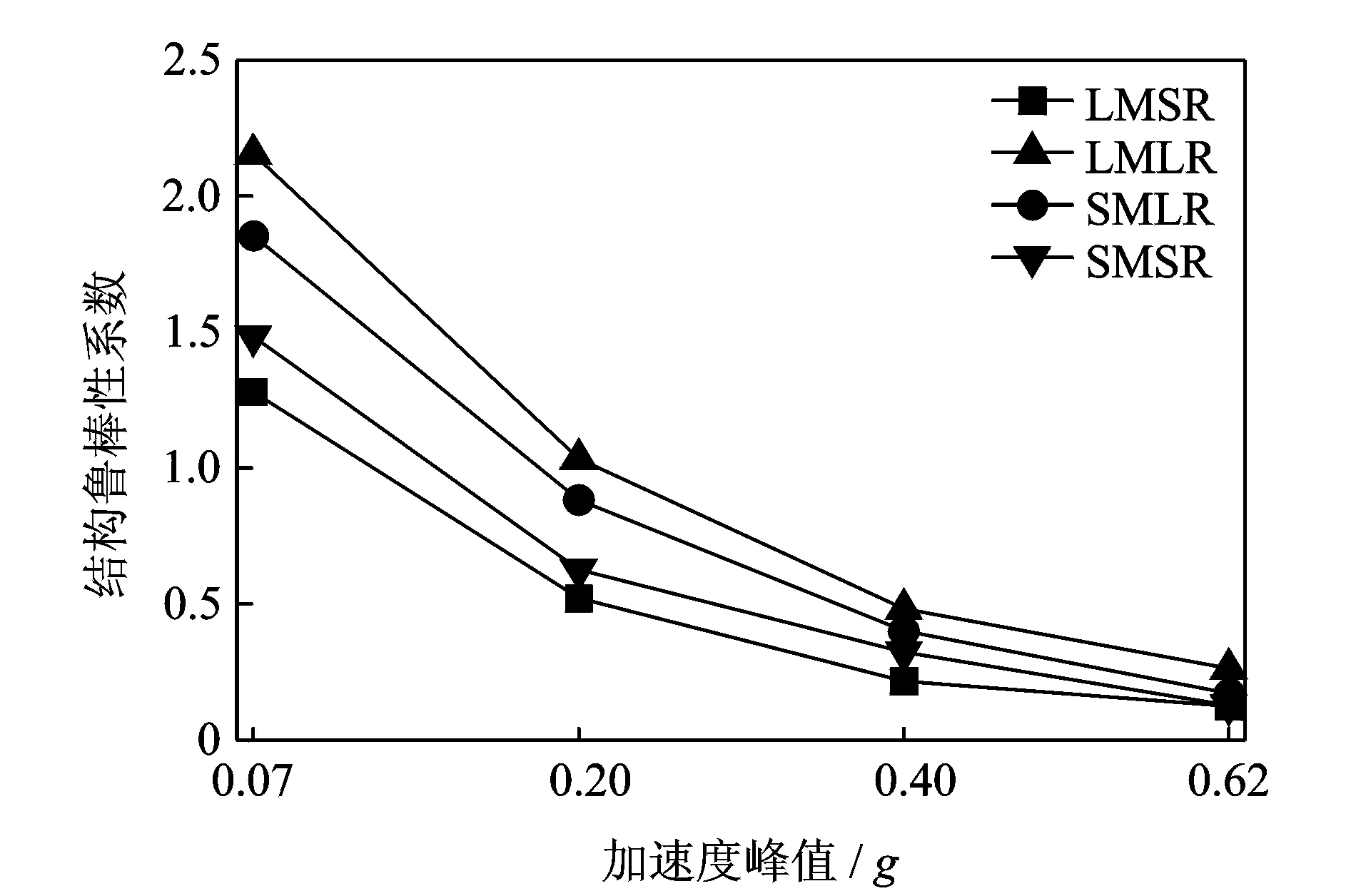
4 结 论

