盘式制动系统参数对制动颤振的影响分析*

2017-03-15李小彭李加胜李木岩闻邦椿

振动、测试与诊断 2017年1期

关键词：初速度摩擦片阻尼

李小彭, 李加胜, 李木岩, 闻邦椿

(东北大学机械工程与自动化学院沈阳， 110819)

盘式制动系统参数对制动颤振的影响分析*

李小彭, 李加胜, 李木岩, 闻邦椿

(东北大学机械工程与自动化学院沈阳， 110819)

为了研究盘式制动系统参数对制动颤振的影响，建立了二自由度的动力学模型，利用Matlab进行数值仿真，分别研究了制动初速度、制动压力、阻尼和刚度等因素对制动系统动力学特性的影响。根据得到的位移曲线和相图可以看出：随着制动初速度的增大，系统黏滞阶段持续时间减少，并逐渐进入稳定运动状态；制动压力相对较小时，制动系统处于稳定状态，随着制动压力的增大，摩擦片和制动盘的振动幅值也随之增大，振动强度变大；在阻尼增大的过程中，摩擦片和制动盘均由起初的纯滑动运动状态进入稳定运动状态，且达到稳定运动状态的时间也逐渐缩短；摩擦片在相对较小的制动刚度下即可达到稳定状态，而制动盘则需要有较大的刚度才能达到稳定状态。

制动系统；动力学模型；数值仿真；制动颤振；稳定状态

引言

振动是评价乘车舒适性的一项重要指标。车辆制动时产生的振动不仅会降低乘车舒适性，还可能引起制动系统零部件的损坏和失效。因此,研究车辆制动系统的动力学特性对提高行车安全和乘车舒适性具有重要意义。

在制动系统摩擦颤振方面，国内外学者进行了研究[1-4]。文献[5]通过有限元法研究了影响制动颤振的一些因素。Crowther等[6]建立了4自由度的线性和非线性系统动力学模型，考虑了制动系统和传动系统的耦合，并用数值方法研究了不同的运动状态。Nishiwaki[7]研究发现，制动噪声是由摩擦力作为非保守力引入系统而使系统动能增量大于零所致。孟宪皆等[8]建立了6自由度的汽车制动盘和摩擦片的非线性动力学模型，并进行稳定性分析。文献[9]研究发现由于制动器的结构因素引起的自激振动是产生制动噪声的主要原因，忽略了材料与制动件之间的摩擦和磨损因素，因而缺乏一定的实际效果。文献[10]对制动噪声进行了研究。Antti等[11]研究发现，制动噪声的主要来源在摩擦界面，摩擦材料是制动尖叫噪声的最大来源之一，可以通过改变摩擦材料来抑制制动噪声。以往关于制动系统摩擦振动的研究大多局限于有限元方法且把制动盘看成是刚体，这种方法有很大的局限性。

笔者以汽车盘式制动器为研究对象，通过建立制动系统的二自由度动力学模型，利用Mtalab进行数值仿真，分析了制动初速度、制动压力、阻尼和刚度等因素对制动系统动态特性的影响，对抑制制动系统的振动和噪声及改善制动系统动力学特性有重要的现实意义。

1 制动系统摩擦模型的建立

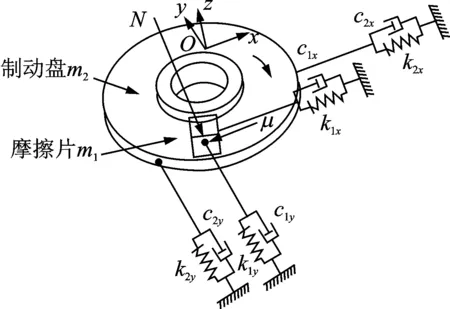
图1 制动系统简化模型Fig.1 Simplified model of the braking system

根据制动盘的实际工作状况，简化制动系统动力学模型如图1所示。在该模型中，制动盘和摩擦片只有在平面内的运动，没有翻转运动。正压力N通过摩擦片施加到摩擦盘上，制动盘是以恒定的角速度绕其质心做圆周运动。摩擦片和制动盘通过摩擦力耦合在一起,其位移x1，x2都是以弹簧无变形时的位置作为基点。图中，m1为摩擦片的质量，m2为制动盘的质量。制动盘和摩擦片分别通过刚度系数为k1x，k2x的弹簧和阻尼系数为c1x，c2x的阻尼单元限制在x方向。同时，制动盘和摩擦片分别通过刚度系数为k1y,k2y的弹簧和阻尼系数为c1y,c2y的阻尼单元限制在y方向。

建立制动系统x方向的动力学模型如图2所示。

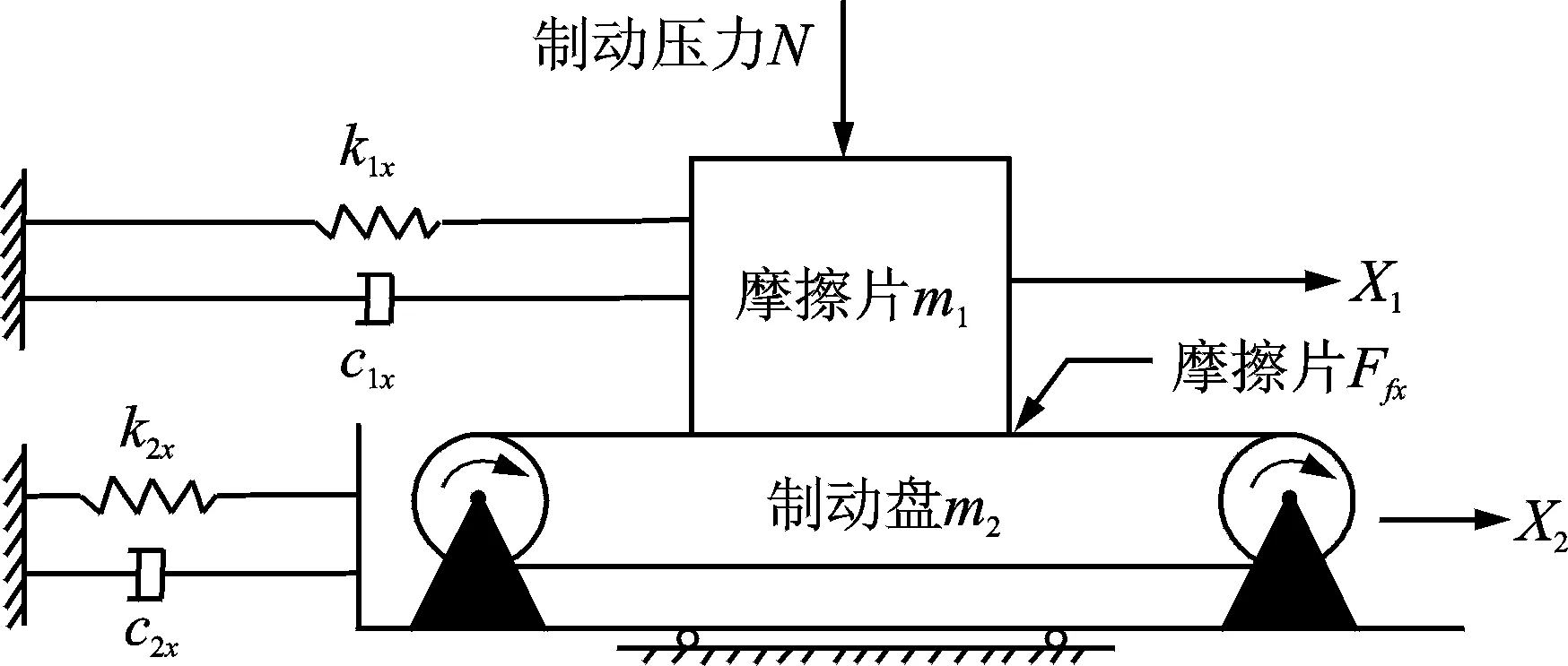
图2 制动系统动力学模型Fig.2 Kinetic model of braking system

对制动系统进行受力分析，得到动力学方程为

(1)

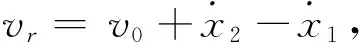
Ffx(vr)=sgn(vr)μ(vr)N

摩擦因数与制动速度的关系为

(2)

其中：γ=0.03;η=0.000 013 463 7;δ=0.05;μs=0.6。

2 制动颤振的影响因素

为了全面了解制动时颤振的动态特性, 需要进行数值仿真。采用控制变量法依次研究制动初速度、制动压力、制动系统刚度和阻尼等参数对制动系统稳定性的影响。

2.1 制动初速度

鉴于定性分析影响盘式制动系统颤振的影响因素,能与黄彩虹等[12]研究结果进行一定的对比，故取以下数值进行仿真分析。仿真参数设定：k1=1 N/m，k2=1 N/m，c1=0.1 (N·s)/m，c2=0.1 (N·s)/m，m1=1 kg，m2=5 kg，N=10 MPa。通过改变制动初速度研究其对制动系统稳定性的影响，制动初速度v0分别取2,12,20,26,40和100 km/h。

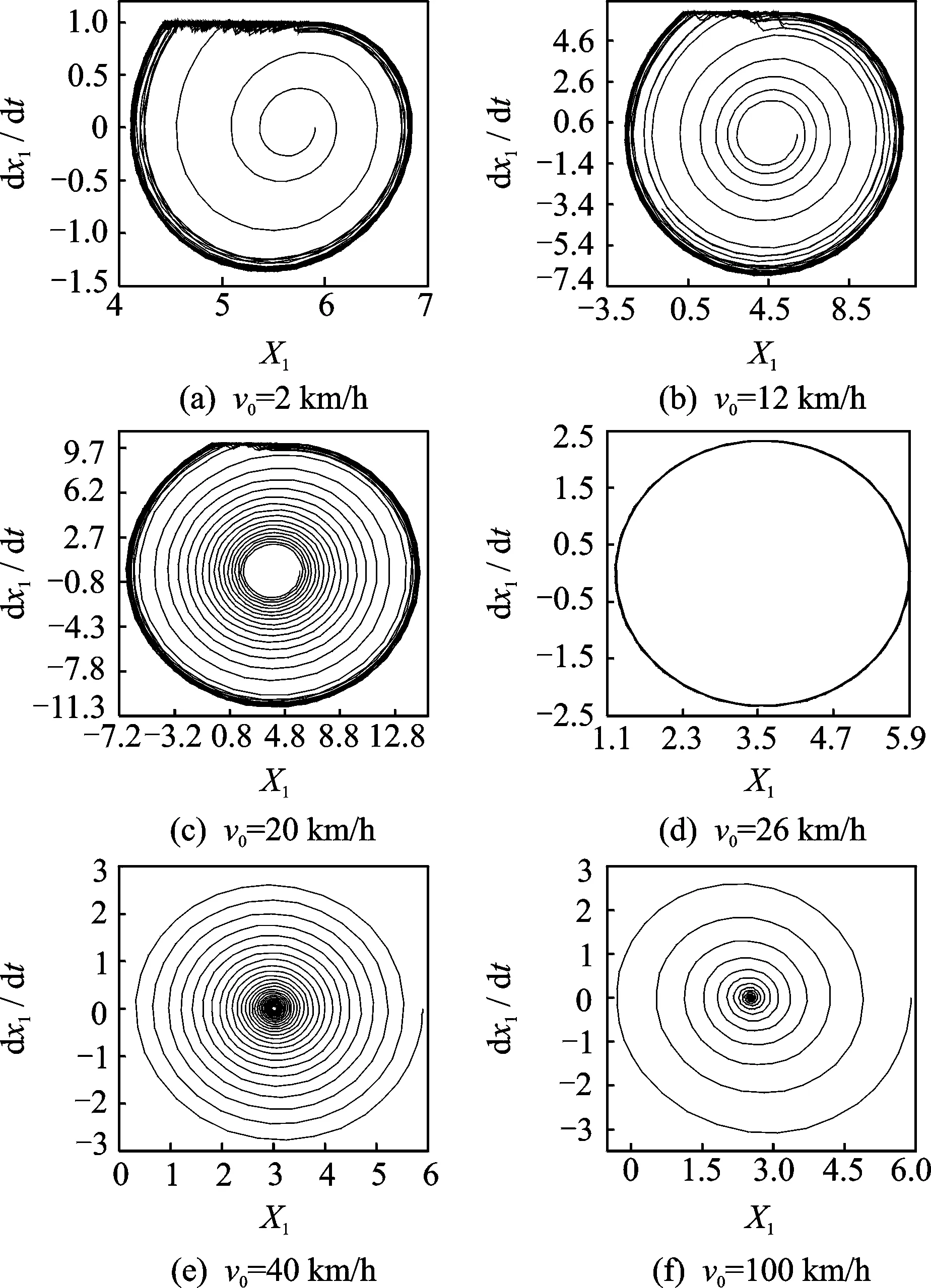
图3 摩擦片在不同制动初速度下的相图Fig.3 The phase diagram of friction plate at different initial velocity

从摩擦片和制动盘相图可以看出，当制动初速度小于26 km/h时，制动系统做准周期运动。制动初速度为2和12 km/h时，出现明显的黏滑现象，制动速度越小，黏滑现象越明显，黏滞阶段持续的时间也更长。当制动初速度为26 km/h时，黏滑现象已基本消失，系统进入无黏滞的周期运动状态。制动初速度大于26 km/h时，系统处于稳定运动阶段，且随着制动初速度的增加，相图中螺旋线的圈数逐渐减小，说明达到稳定状态的周期越来越短。可见，提高制动初速度有助于缩短达到稳定状态的时间。

图4 制动盘在不同制动初速度下的相图Fig.4 The phase diagram of brake disc at different initial velocity

2.2 制动压力

仿真参数设定：k1=1 N/m，k2=1 N/m，c1=

0.1 (N·s)/m，c2=0.1 (N·s)/m，m1=1 kg，m2=5 kg，v0=26 km/h。通过改变摩擦片和制动盘所受的制动压力，观察其位移曲线及相图的变化情况。制动压力N分别取5,30和50 MPa。

从摩擦片和制动盘的位移曲线可以看出，随着制动压力逐渐增大，摩擦片的位移幅值也逐渐增大。制动压力小于30 MPa时，摩擦片初始位移幅值较大，但很快达到稳定状态。制动盘的位移曲线与摩擦片的类似，但达到稳定状态的时间比较长。制动压力大于30 MPa时，摩擦片基本处于等幅振动状态,制动盘位移曲线极其不规则，振动没有规律。

从摩擦片和制动盘的相图可以看出，在制动压力比较小时，制动盘和摩擦片均处于稳定状态。随着制动压力的增大，摩擦片由纯滑动阶段逐渐进入黏滑运动状态，并且随着制动压力的增大，黏滞阶段持续的时间也逐渐增长。在制动压力较大时，制动盘的相图曲线变得无规则，振动状态也比较复杂。

2.3 阻尼

仿真参数设定：k1=1 N/m，k2=1 N/m，m1=1 kg，m2=5 kg，N=10 MPa，v0=26 km/h。通过改变摩擦片和制动盘的阻尼，观察各自对应的相图变化情况。阻尼分别为c1=0.1 (N·s)/m，c2=0.1 (N·s)/m,c1=0.2 (N·s)/m，c2=0.4 (N·s)/m,c1=0.5 (N·s)/m，c2=0.9 (N·s)/m。

从摩擦片和制动盘的相图可以看出，在阻尼较小时，摩擦片和制动盘的相图为不存在黏滞阶段的极限环，系统的运动形式为纯滑动运动。随着阻尼的增大，系统将逐渐稳定在平衡点上，此时系统进入稳定状态，且阻尼越大，系统达到稳定时所需要的时间越短。

图5 摩擦片在不同制动压力下的位移曲线Fig.5 The displacement curve of friction plate at different braking pressure

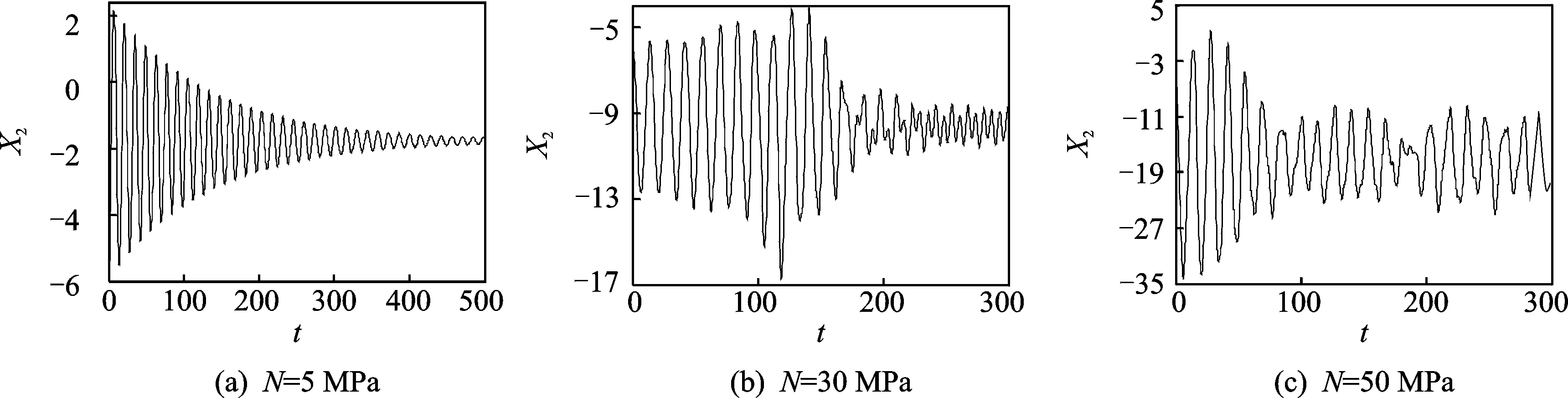
图6 制动盘在不同制动压力下的位移曲线Fig.6 The displacement curve of brake disc at different braking pressure

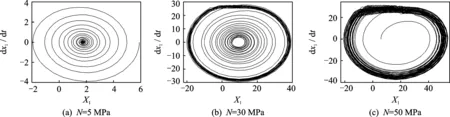
图7 摩擦片在不同制动压力下的相图Fig.7 The phase diagram of friction plate at different braking pressure

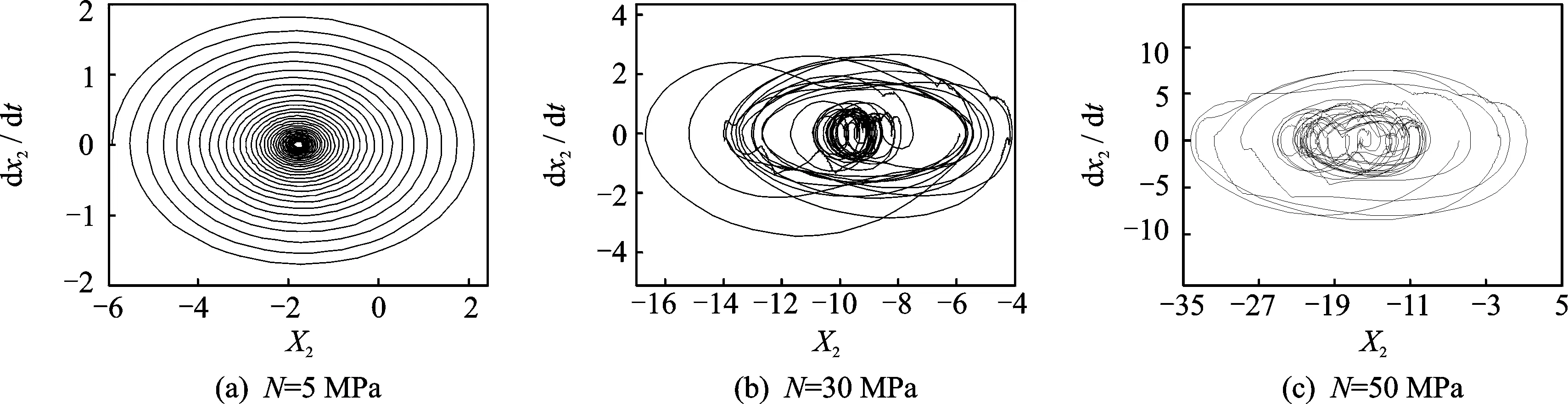
图8 制动盘在不同制动压力下的相图Fig.8 The phase diagram of brake disc at different braking pressure

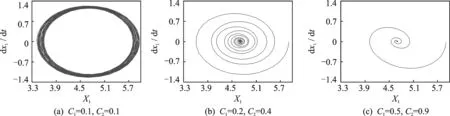
图9 摩擦片在不同阻尼比下的相图Fig.9 The phase diagram of friction plate at different damping coefficient

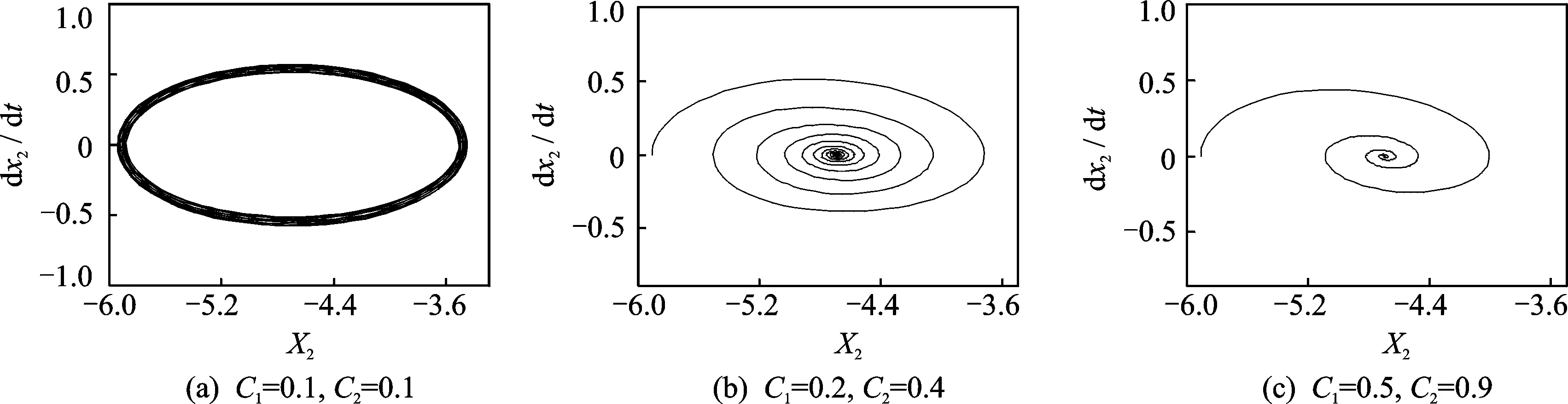
图10 制动盘在不同阻尼比下的相图Fig.10 The phase diagram of brake disc at different damping coefficient

2.4 刚度

仿真参数设定：m1=1 kg，m2=5 kg，N=10 MPa，v0=26 km/h，c1=0.5 (N·s)/m，c2=0.1 (N·s)/m。通过改变摩擦片和制动盘的刚度，

图11 k1=1 N/m，k2=3 N/m 摩擦片的位移时间曲线、速度时间曲线与相图Fig.11 Displacement-time curve, velocity-time curve and phase diagram of friction plate when k1 is 1 N/m and k2 is 3 N/m

图12 k1=40 N/m，k2=100 N/m 摩擦片的位移时间曲线、速度时间曲线与相图Fig.12 Displacement-time curve, velocity-time curve and phase diagram of friction plate when k1 is 40N/m and k2 is 100 N/m

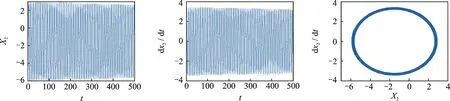
图13 k1=1 N/m，k2=3 N/m 制动盘的位移时间曲线、速度时间曲线与相图Fig.13 Displacement-time curve, velocity-time curve and phase diagram of brake disc when k1 is 1 N/m and k2 is 3 N/m

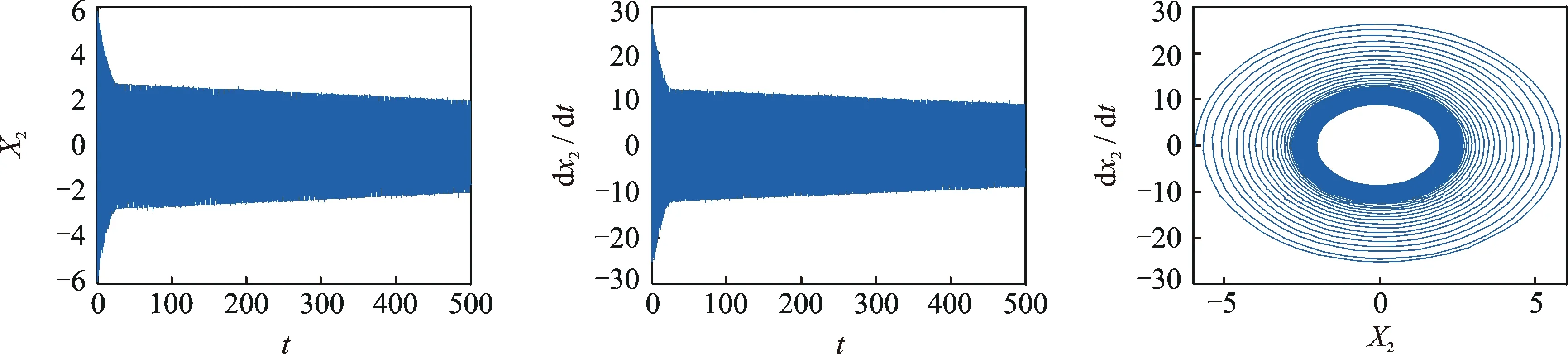
图14 k1=40 N/m，k2=100 N/m 制动盘的位移时间曲线、速度时间曲线与相图Fig.14 Displacement-time curve, velocity-time curve and phase diagram of brake disc when k1 is 40 N/m and k2 is 100 N/m

观察其各自对应的位移曲线和相图的变化情况。刚度值分别取k1=1N/m,k2=3N/m和k1=40N/m,k2=100N/m两种情况。

从摩擦片和制动盘的位移曲线可以看出，在刚度较小时，摩擦片的初始位移振幅比较大，之后以某一稳定振幅振动，随着刚度增大，摩擦片运动状态逐渐趋于稳定；在刚度较小时，制动盘做等幅振动，随着刚度增大，制动盘位移幅值逐渐减小，但减小的速度比较慢。

从摩擦片和制动盘的相图可以看出，在系统刚度较小时，摩擦片和制动盘的相图均为无黏滞阶段的极限环。随着刚度增大，摩擦片首先进入稳定状态，而制动盘的准平衡点开始沿着轨迹向内侧运动，直到遇到内侧稳定的纯滑动极限环后，逐渐融合在稳定的极限环中。

刚度较小时，系统的准静态平衡点不稳定，此时系统的运动为不稳定的平衡点和稳定的极限环的综合运动；当刚度达到一定值时，系统的准静态平衡点开始变得稳定，此时极限环仍然存在，系统的运动是稳定平衡点的运动和稳定极限环的综合运动。

3 结论

1) 制动初速度相对较小时，系统存在明显的黏滑振动现象，随着制动初速度的增加，黏滞阶段持续时间逐渐减小，进入纯滑动运动状态，随着制动初速度的继续增加，系统最终进入稳定状态。

2) 制动压力相对较小时，制动系统处于稳定状态，随着制动压力的增大，摩擦片和制动盘的振动幅值也随之增大，振动强度变大。

3) 在阻尼增大的过程中，摩擦片和制动盘均由起初的纯滑动运动状态进入稳定状态，且达到稳定运动状态的时间也逐渐缩短。同时还可以得出，仅增大制动盘的阻尼而不改变摩擦片的阻尼时，系统的振动稳定性并未得到改善，而在同时增大制动盘和摩擦片的阻尼时，系统振幅均减小并最终达到稳定状态。

4) 摩擦片在相对较小的制动刚度下可以达到稳定状态，而制动盘则需要有较大的刚度才能达到稳定状态。因此在结构设计选材时，摩擦片可以选用相对较小的刚度，而制动盘选用相对较大的刚度来提高制动稳定性。

[1] Nakae T, Ryu T, Sueoka A, et al. Squeal and chatter phenomena generated in a mountain bike disc brake [J]. Journal of Sound and Vibration, 2011, 330(10):2138-2149.

[2] Oberst S, Lai J C S. Nonlinear transient and chaotic interactions in disc brake squeal [J]. Journal of Sound and Vibration, 2015, 342(4):272-289.

[3] 刘献栋，任增杰，王海霞，等. 盘式制动器摩擦特性及制动尖叫测试与分析[J]. 振动、测试与诊断，2013，33(5)：746-750.

Liu Xiandong，Ren Zengjie，Wang Haixia，et al. Disc brake friction characteristics, braking scream test and analysis [J]. Journal of Vibration, Measurement & Diagnosis，2013，33(5)：746-750. (in Chinese)

[4] 孟德建，张立军，余卓平. 多点接触模型的盘式制动器制动抖动分析[J].

振动、测试与诊断, 2010, 30(3):

304-309.

Meng Dejian, Zhang Lijun, Yu Zhuoping. Analysis of disc brake judder using multipoint contact dynamic mode [J]. Journal of Vibration, Measurement & Diagnosis, 2010, 30(3):304-309.(in Chinese)

[5] Brecht J, Hoffrichter W, Fohle A.Mechanisms of brake creep groan[J]. Sae Technical Papers, 1997,106(2):3405-3411.

[6] Crowther A R, Rajendra S. Analytical investigation of stick-slip motions in coupled brake-driveline systems [J]. Nonlinear Dynamics, 2007, 50(3): 463-481.

[7] Nishiwaki M.Generalized theory of brake noise[J].Journal of Automobile Engineering, 1993, 207(3):195-202.

[8] 孟宪皆，吴光强. 汽车制动盘和摩擦片振动的数值解 [J]. 江苏大学学报，2011，32(3): 292-296.

Meng Xianjie,Wu Guangqiang. Numerical solution for vibration behavior of automotive brake disc and pads [J]. Journal of Jiangsu University, 2011，32(3): 292-296.(in Chinese)

[9] Gao Huijun, James L, Wang Changhong . Multi-objective control of vehicle active suspension systems via load-dependent controllers [J]. Journal of Sound and Vibration, 2005,29(3): 654-675.

[10]Yu S D, Wen B C. Vibration analysis of multiple degrees of freedom mechanical system with dry friction [J]. Proceedings of the Institution of Mechanical Engineers, 2013, 227(7):323-336.

[11]Antti P, Joseph C S L, Zhao Jiye,et al. Brake squeal: a literature review [J]. Applied Acoustics, 2002, 63(4): 391-400.

[12]黄彩虹,曾京. 利用黏滑机理分析铁道车辆盘形制动颤振 [J]. 现代制造工程,2009(5):26-28,105.

Huang Caihong, Ceng Jing.Analysis of disk braking flutter for rolling stock based on stick-slip theory [J]. Modern Manufacturing Engineering, 2009(5):26-28,105.(in Chinese)