基于CFSPSO算法的控制器参数优化

孙海蓉，田 瑶,b，谢碧霞,b，靳 鑫

(华北电力大学 a.控制与计算机工程学院；b.河北省发电过程仿真与优化控制工程技术研究中心，河北保定071003)

基于CFSPSO算法的控制器参数优化

孙海蓉a，田 瑶a,b，谢碧霞a,b，靳 鑫a

(华北电力大学 a.控制与计算机工程学院；b.河北省发电过程仿真与优化控制工程技术研究中心，河北保定071003)

针对基本粒子群优化参数性能的不足及其优化算法易早熟的弊端，提出一种带压缩因子的二阶粒子群改进算法(CF-SecPSO)。采用多种测试函数对改进算法进行测试，同时介绍控制器参数优化时目标函数的选取，将算法应用于电厂主汽温控制系统控制器参数优化中。仿真研究表明：与基本粒子群算法和带压缩因子粒子群(CFPSO)算法相比，改进的粒子群算法改善了算法的搜索速度及精度，有效避免陷入局部最优。将其应用于优化主汽温的PID串级控制器参数，改进算法提升了控制系统的性能，对实际控制系统中参数整定提供了重要参考，验证了该算法的适用性。

控制系统；参数优化；PSO；压缩因子；主汽温

0 引言

传统PID控制器结构简单[1,2]、易于实现、具有明确的参数定义和稳定控制性能，在多数工业控制系统中具有广泛应用。PC技术带动了智能控制理论的快速发展，采用先进控制理论对传统算法进行优化成为研究热点。PSO算法作为智能算法中计算迅速、容易实现的算法在控制器参数优化中体现了巨大优越性。文献中对其改进的算法大都采用优化效果单一的单策略改进，改进后算法的收敛速度及易早熟的缺陷得到一定程度改善[3,4]，但并不能使其脱离局部收敛的困境，如何协调局部搜索和全局搜索能力是PSO算法改进的主要切入点。就具有多扰动大迟延等特点的主汽温对象而言，PID控制器参数的整定优化备受关注。

针对PSO算法易早熟的弊端，本文在基本PSO算法的基础上，提出带有压缩因子的二阶粒子群算法(CF-SecPSO)，采用多种标准测试函数对算法进行测试，分析比较算法在改善早熟及提高算法速度等方面的性能。文中将CFSPSO算法应用于主汽温被控对象PID控制器参数优化中，验证算法在参数优化中的适用性及优越性。

1 带压缩因子二阶粒子群算法

为提高粒子种群多样性、准确性及灵敏性，进一步改善算法性能，本文在基本PSO算法基础上，提出了带压缩因子的二阶粒子群改进算法。

1.1 CF-SecPSO算法描述

(1)惯性权重算法的选取

粒子群算法惯性权重体现了算法对于局部搜索和全局搜索的平衡能力[5,6]。现今常用惯性权重改进方法有：采用不同的初始惯性权重；线性递减惯性权重法[7]；非线性惯性权重法[8,9]等。由于本文采用压缩因子已经对速度更新进行了加权，故本文中可取惯性权重ω为1。

(2)带压缩因子的二阶粒子群算法

对学习因子c1、c2设置影响分析可知，微粒自身经验学习与种群中粒子间的信息共享是算法寻优的优势所在。粒子飞行速度是算法是否能够找到最优解的关键。由此，Clerc引入了带压缩因子的PSO算法，速度更新规则为[10-12]：

(1)

(2)

称式(1)中算法为带压缩因子的粒子群算法[13,14]。

在基本PSO算法中，粒子飞行速度是由个体当前位置与个体最优位置和全局最优位置的距离随机线性加权而得，如式(1)所示。即当粒子的个体最优位置与全局最优位置固定时，粒子飞行速度仅为其当前位置的函数。而实际的粒子飞行速度变化还应与粒子位置变化(Xi(t)-Xi(t-1))有关，即粒子的速度更新与粒子的实际速率相关。当pbest与gbest确定时，若只考虑粒子飞向pbest，则该粒子目标速率Vp理论为pbest-Xi，但此时粒子实际速率Vx为Xi(t)-Xi(t-1)，故粒子的速度变化率为：

pbest-2Xi(t)+Xi(t-1)

(3)

同理，只考虑粒子飞向gbest时，则理论上该粒子目标速率Vg为gbest-Xi，而实际所得粒子速度变化率为：

gbest-2Xi(t)+Xi(t-1)

(4)

当粒子将个体极值与全局极值同时进行考虑时，粒子速度变化率为分别考虑粒子飞向个体最优和全局最优位置距离的随机加权，即

Vi(t+1)=Vi(t)+c1(pbest-2Xi(t)+

(5)

结合式(1)中对加速因子的改进，为使粒子的速度更新更贴合实际，在此基础上引入上一时刻粒子位置为当前粒子速度的更新作参考，仿真研究发现，当对于上一时刻粒子不分好坏都进行参考时，不仅算法速度会下降，算法精度也变差。因此，本文在带压缩因子粒子群算法的基础上，提出了CF-SecPSO算法对上一时刻的粒子进行选择性参考，引入一个可调整因子，在速度更新过程中，对于上一时刻迭代中产生的粒子好值进行一定程度参考，指导算法的优化方向，使其避免陷入局部最优。故可提出CF-SecPSO算法的速度更新公式为：

aXi(t-1))+c2(gbest-(1+a)Xi(t)+

(6)

即式(6)为带压缩因子的二阶粒子群算法(CFSPSO)速度更新规则。

1.2 算法流程及参数设置

Step1：初始化。初始化粒子，定义种群大小、粒子维度和迭代次数。设定搜索点的初始位置及速度，一般在许可范围内随机选择。

Step2：评价种群。依据预先选择设定的目标函数求解粒子适应度值，评价初始种群。

Step3：更新粒子。用式(6)与式(2)对种群中所有个体速度和位置进行更新。

Step4：判断算法是否满足结束条件。如果迭代次数达到预先设定最大值(或取得足够好的适应度，或最优解停滞不再变化)，终止迭代，输出最优解及粒子群体最小适应度，否则转Step3，更新粒子，继续迭代直至满足结束条件，输出最优解。

类似于标准PSO算法，带压缩因子的二阶粒子群CF-SecPSO算法需设置加速常数c1、c2、惯性权重，以及群体规模M、最大速度Vmax和最大进化代数T等参数，由于引入的压缩因子已经对速度更新进行加权，故惯性因子设置为1。当c1+c2大于4，调整因子取为0.2时，仿真验证表明，此改进算法具有较好的收敛性，其他参数设置同基本PSO算法一致。

2 算法测试及精度比较

智能优化算法按照某种规则或者思想进行搜索来得到满足要求的解[15]。较快的寻优速度和较高的寻优精度是判断算法是否具有良好优化性能的重要指标，同时对于优化算法的测试也是算法改进的一个重要内容。智能算法常用测试函数有很多种，根据需要本文选用5个经典测试函数如表1所示，分别是利用Sphere函数、Rastrigrin函数、Schwefel2.21函数、Griewank函数和Step函数来进行算法性能测试，5个测试函数的最小值均为0，如表1所示。其中Griewank函数存在许多局部极小点，其数目与问题的维数有关，属于非线性多模态函数且具有广泛的搜索空间，通常被认为是优化算法很难处理的复杂多模态问题。Rastrigrin函数也属于非线性多模态函数。利用上述函数对所提出的CF-SecPSO算法性能进行测试及比较，验证算法的普适性。同时根据算法的改进特点，选取两种具有代表性的测试函数对算法进行进一步的测试及比较。

表1 5个测试基准函数

为了比较的公平性所有算法都设置相同的最大目标函数评价次数为2.5×105次，其他参数可参考文献进行设置，在种群规模为50，种群维度为N=10的情况下用测试函数对算法依次进行测试，每个算法程序各运行30次，并对寻优结果的最小值、最大值和平均值及方差进行统计，比较其大小并对算法的优化性能进行评价，整理测试结果如表2所示。

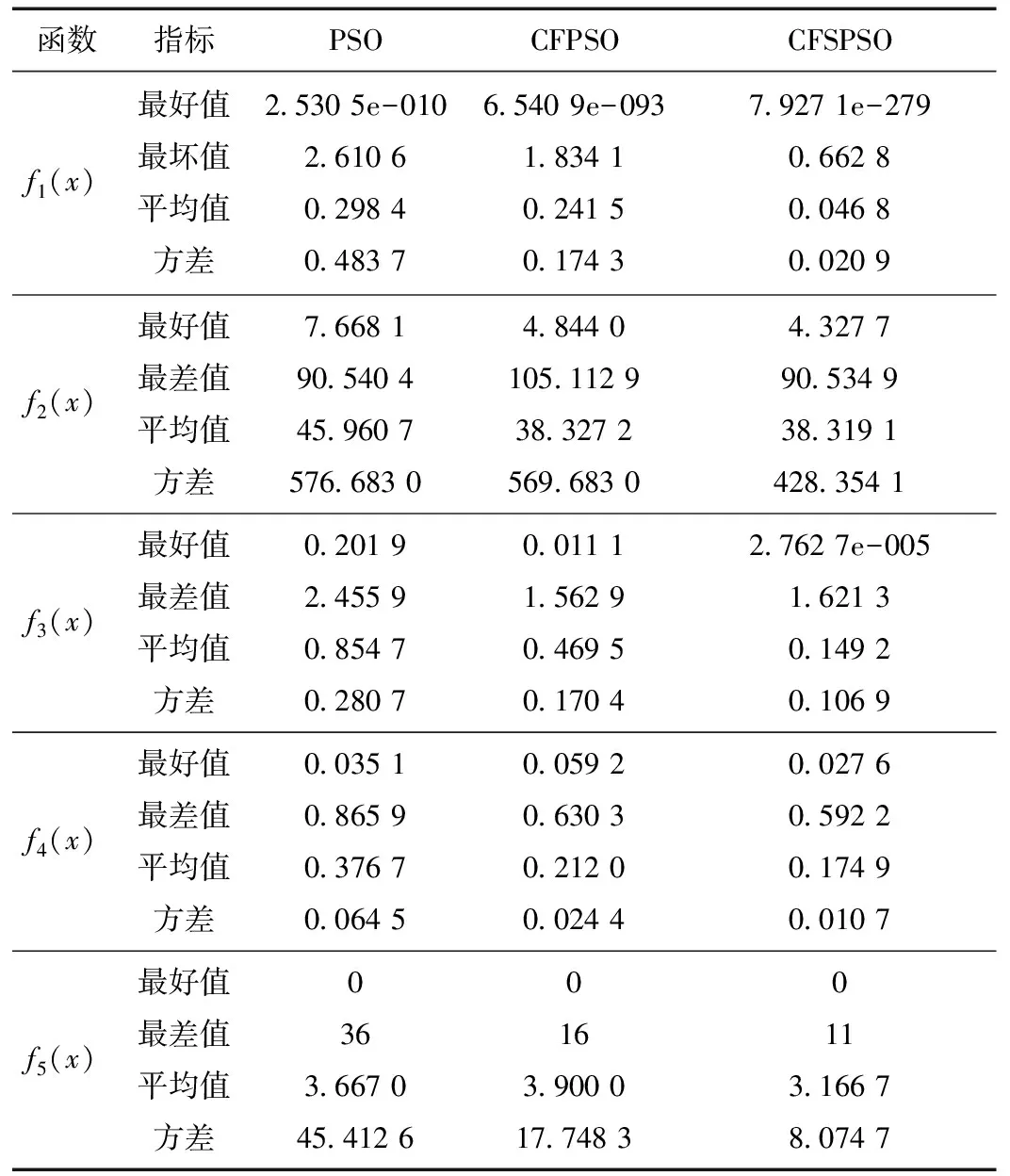
表2 测试函数结果比较(N=10)

表1中Sphere函数是典型线性单模态函数，在整个搜索空间中有多个局部最小值，但只有一个全局极小值，通常用该函数测试算法的执行性能。Rastrigrin函数属于非线性多模态函数[4]3，在搜索空间中存在大量极小值和障碍物，使算法更容易陷入局部收敛，通常可用来检验算法是否能够克服局部收敛。这2个测试函数极具有代表性，在参数维度较低时对算法进行进一步的测试及比较，测试结果如表3所示(设置最大目标函数评价次数为1×104次)。

表3 测试函数结果比较(N=3)

CF-SecPSO算法无论在最好值、平均值、最差值、方差方面都优于PSO算法及带压缩因子的粒子群(CFPSO)算法，在相同迭代次数限制下，改进之后算法精度得到了较大改善。

若优化单模态函数，在低参数量和高参数量情况下，CF-SecPSO算法与CFPSO算法搜索精度相较于PSO算法有很大提高，且更加精确，粒子群早熟现象有很大改善。若优化多模态函数，在低参数量时，CF-SecPSO算法优化精度比CFPSO算法和PSO算法更精确；但在高参数量时，CF-SecPSO算法与CFPSO算法搜索精度相近，且相较于基本PSO算法有明显提升。

3 仿真试验

某电厂300 MW机组的主汽温系统采用两级喷水减温进行调节，每一级喷水减温都分A、B两侧，且均采用串级控制[16,17]。由于本文主要研究粒子群优化算法及其仿真，其他对汽温的影响因素如燃料量、负荷变化等本文不予讨论，简化后主汽温串级控制原理图如图1所示。

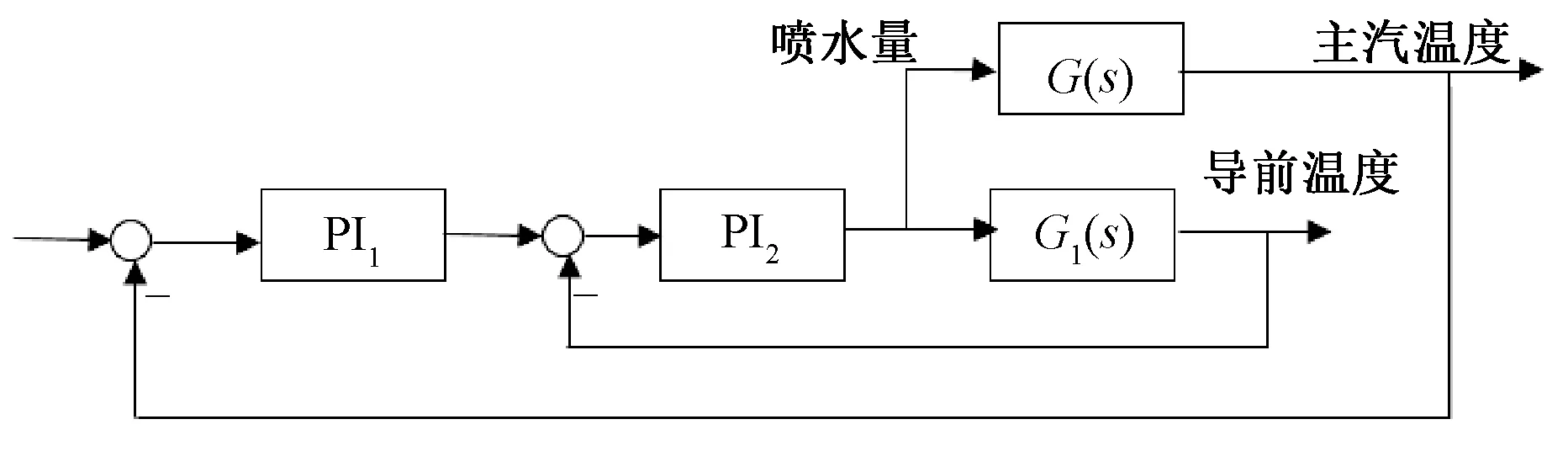
图1 简化后主汽温串级控制原理图

主汽温对象具有大迟延[18]、非线性、时变、受干扰因素多等特点，其优化问题涉及到结构优化及参数优化等诸多方面，本文的研究内容为串级控制中主副回路PI控制器的参数优化问题，其中汽温控制对象的传递函数取为：

3.1 目标函数选取及参数设置

在实际工程应用中，控制系统的性能指标是衡量系统控制效果的准则，优化算法中目标函数的选取对控制系统工作性能的判定有很大影响。工程应用中常有2种选取方法，包括调节品质型目标函数和误差积分型目标函数[19]。对于同一控制系统，按不同的积分准则进行优化所得系统响应也不同。对于PID控制器参数优化而言，调节品质型目标函数可能存在调节或振荡时间较长的弊端，故常选用误差积分型目标函数。

误差积分型目标函数是基于被调量与给定值之间偏差的积分函数，有3种比较常见的形式：分别是平方误差积分准则(ISE)、时间乘平方误差准则(ITSE)及时间乘绝对误差积分准则(ITAE)。对于同一系统采用不同的积分准则对应的系统响应也不同。在采用误差积分准则进行优化控制器参数时，会发现有的参数虽能使系统获得较好的响应指标，但调解过程中可能出现控制器输出调节幅度过大或者存在剧烈震荡的现象，不利于现场过程的控制。为避免此类现象的发生同时防止控制能量出现过大的变化，可对误差目标函数进行修正，在误差积分准则ITAE的基础上加入控制器输出量的绝对值以避免输出量变化过大。目标评价函数取能反映系统调节品质的积分函数，表达式为：

式中：c1=0.02，c2=0.98；Q值为目标函数值。用智能优化算法优化主副回路PID控制器的参数时，可将控制器参数取值区间设为LLimits=[0.5,40,0.1,20]，HLimits=[3,200,2,120]；相应粒子速度变化范围为Vmax=[0.1,2,0.1,2]；粒子种群规模M=50；迭代次数S=100；基本PSO算法学习因子为c1=c2=2，惯性权重ω=0.5，而CF-SecPSO算法和CFPSO算法学习因子取为c1=c2=2.05，可调整因子为0.2，惯性权重ω=1；系统采样周期及采样点数为DT=1，LP=3 000。

3.2 仿真结果

采用上述设置参数对控制系统进行仿真实验，可得3种粒子群优化算法优化PID控制器参数如表4所示，所得控制系统阶跃响应曲线如图2～5所示。

表4 寻优前后的控制器参数

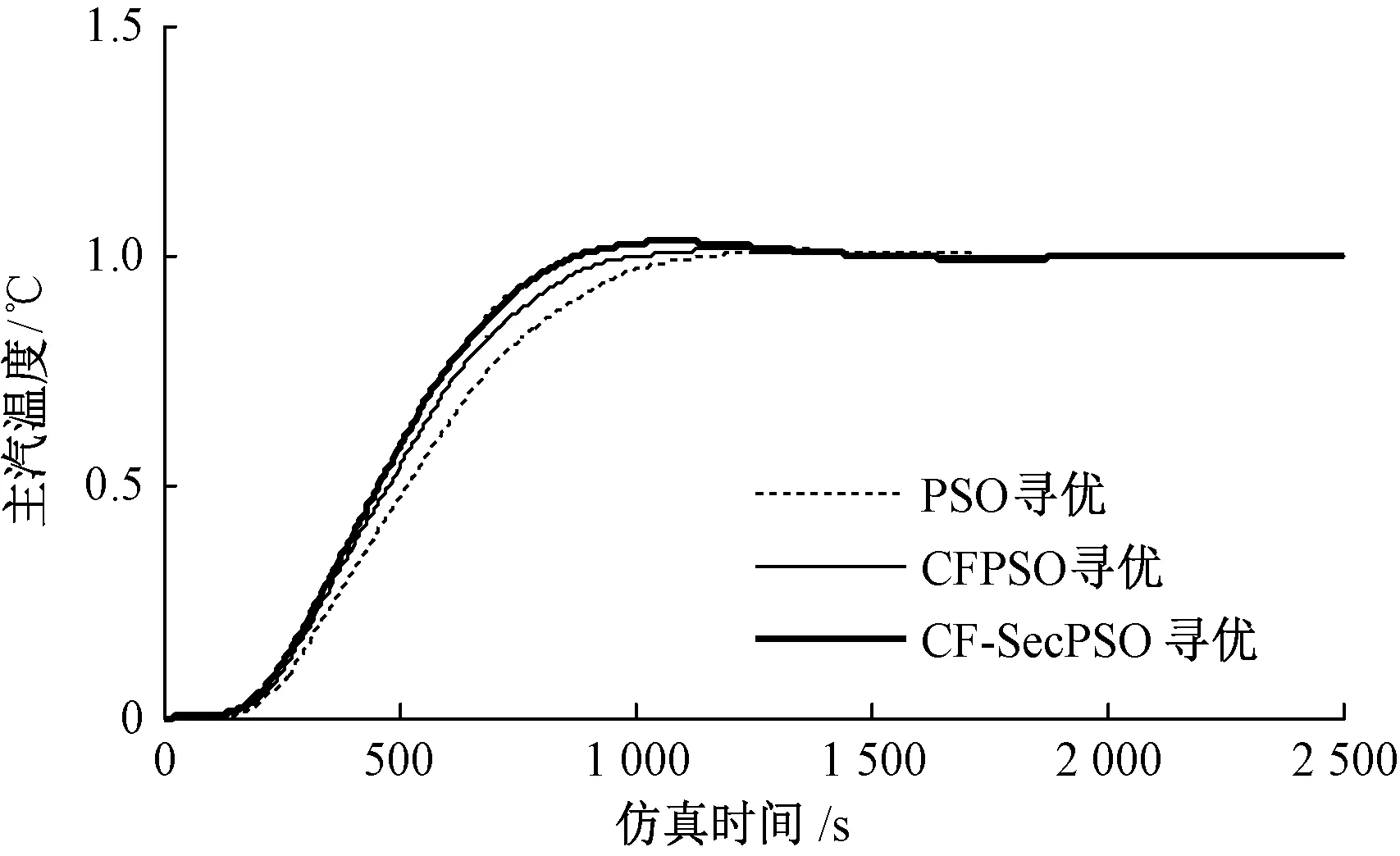
图2 3种PSO算法的主汽温度对比图

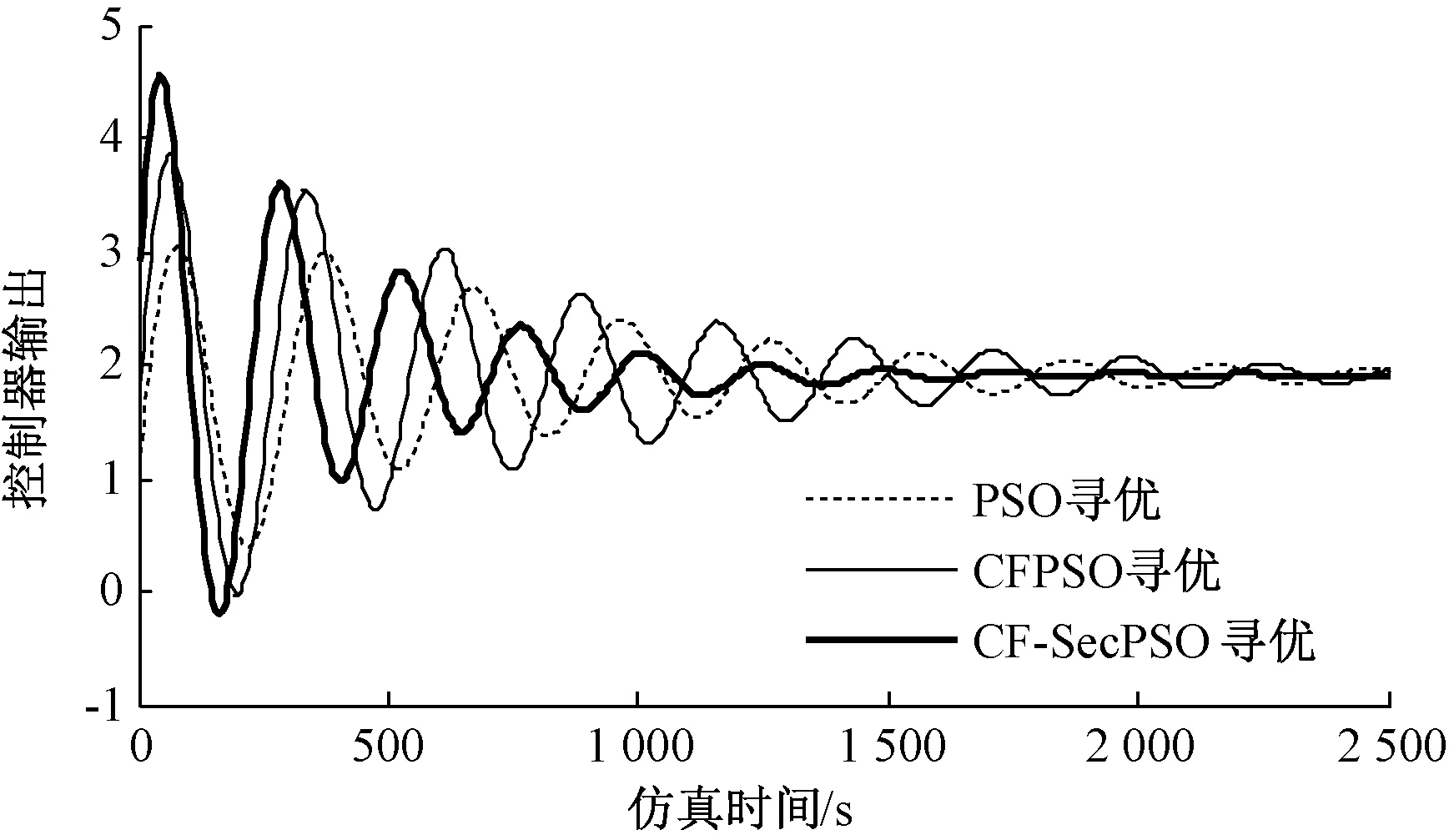
图3 3种PSO算法的控制器输出对比图

图4 3种PSO算法的导前温度对比图

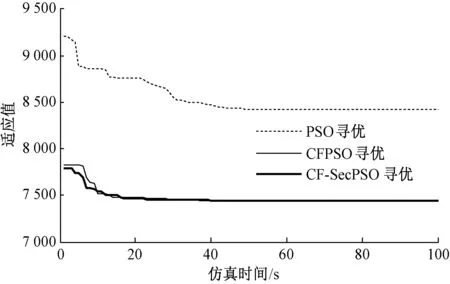
图5 3种PSO算法的粒子适应度对比图

3.3 结果分析

(1)由图2可以看出，主汽温控制稳定时间ts减小，快速性变好，综合考虑控制系统品质指标时，常需牺牲某一指标来达到目标函数最优，故寻优结果符合要求，且得到较好效果。

(2)由图5可知，改进后的粒子适应值降低，较基本粒子群而言，迭代粒子取得更好值，避免陷入局部最优。

(3)由仿真结果可见，系统阶跃响应速度变快，控制器输出初始时虽震荡较大但较快收敛，算法搜索速度得到改善。从导前温度响应曲线看，导前温度控制的稳定性与快速性有明显提高。

在控制系统中，主汽温串级控制系统PID控制器参数整定中涉及4个参数，带压缩因子的二阶粒子群(CF-SecPSO)算法无论从搜索速度和搜索精度上均优于其他2种粒子群算法，从而验证了该改进算法的有效性和适用性。

4 结论

本文所提出的带压缩因子的二阶粒子群算法，在粒子的速度更新中对上一时刻迭代产生的粒子好值进行一定程度的参考，使得算法能够快速地迭代出最优解，改善基本粒子群易早熟的缺陷。优化测试结果表明，CF-SecPSO算法能够提高算法准确性，克服基本粒子群算法中种群易早熟收敛及陷入局部最优解的现象。利用该算法整定PID控制器参数，控制系统调整时间变短，响应时间加快，系统的鲁棒性增强，该算法具有现实意义。同时，其优化性能也更佳，可广泛应用于参数的在线整定、网络优化、图像处理、智能机械优化设计等多个方面。

[1]李剑波，王东风，付萍，等. 基于改进粒子群算法的主汽温系统PID参数优化[J]. 华北电力大学学报(自然科学版)，2015，32(4)：26-30.

[2]郭文忠，陈国龙. 离散粒子群优化算法及其应用[M]. 北京：清华大学出版社，2012：58-64.

[3]刘建华. 粒子群算法的基本理论及其改进研究[D].长沙：中南大学，2009.

[4]王皓，欧阳海滨，高立群. 一种改进的全局粒子群优化算法[J]. 控制与决策，2016，31(7)：1161-1168.

[5]任雪婷，贺兴时. 一种改进的粒子群与差分进化混合算法[J]. 西安工程大学学报，2016，30(3)：380-387.

[6]KENNEDYJ,EBERHARTR.Particleswarmoptimization[C]. //IEEEInternationalConferenceonNeuralNetworks,Piscataway, 1995: 1942-1948.

[7]白国振，荆鹏翔. 基于改进粒子群算法的并联机械手运动学参数辨识[J]. 信息与控制，2015，44(5)：545-551.

[8]韦根原，冯新强，韩璞. 基于CQPSO算法的控制系统参数优化[J]. 系统仿真学报，2015，27(7)：1570-1576.

[9]周美兰，张宇，杨子发，等. 带压缩因子粒子群优化的混合动力汽车模糊能量管理策略[J]. 电机与控制学报，2011，15(11)：67-72.

[10]黄松，田娜，纪志成. 基于自适应变异概率粒子群优化算法的研究[J]. 系统仿真学报，2016，28(4)：874-879.

[11]黄璇，郭立红，李姜，等. 改进粒子群优化BP神经网络的目标威胁估计[J]. 吉林大学学报(工学版)，2016，46(2)：1-6.

[12]张捍东，陶刘送. 粒子群优化BP算法在液压系统故障诊断中应用[J]. 系统仿真学报，2016，28(5)：1186-1190.

[13]张成兴. 时变压缩因子粒子群算法[J]. 计算机工程与应用，2015，51(23)：59-64.

[14]刘长良，高亚龙. 带压缩因子的粒子群算法在汽包压力控制系统中的应用[J]. 计算机系统应用，2012，21(1)：164-167.

[15]宫华，袁田，张彪. 基于深度邻域搜索PSO算法的装配序列优化问题[J]. 控制与决策，2016，31(7)：1291-1295.

[16]范成礼，邢清华，范海雄，等. 带审敛因子的变邻域粒子群算法[J]. 控制与决策，2014，29(4)：696-700.

[17]焦嵩鸣，谭雨林，桑士杰. 基于改进粒子群算法的主汽温控制系统PID参数优化[J]. 电力科学与工程，2012，28(12)：9-13.

[18]王文兰，王巍，崔艳艳. 改进PSO算法优化超临界机组主汽温参数的研究[J]. 广东电力，2013，26(10)：3-18.

[19]韩璞，董泽，王东风，等. 智能控制理论及应用[M]. 北京：中国电力出版社，2012：39-47.

Parameter Optimization of Controllor Based on CFSPSO Algorithm

SUN Haironga, TIAN Yaoa,b, XIE Bixiaa,b, JIN Xina

(a. School of Control and Computer Engineering; b. Hebei Engineering Research Center of Simulation & Optimized Control for Power Generation, North China Electric Power University, Baoding 071003, China)

In order to improve the performance of the optimized parameters of the basic particle swarm optimization and avoid the disadvantages of the optimization algorithm, a new algorithm for the two order particle swarm optimization with compression factor (CF-SecPSO) is proposed. Several test functions are used to test and analyze the algorithm. The accuracy of improved particle swarm algorithm is verified, and the problem of local optimum is avoided. At the same time, the algorithm is applied to optimize the control parameters, compared with the traditional particle swarm algorithm and the compression factor of the particle swarm algorithm(CFPSO), and the performance of the PID control system can be greatly improved, which verifies the practicability of the algorithm.

control system; optimizated parameter; PSO; compression factor; main steam temperature

10.3969/j.ISSN.1672-0792.2017.02.013

2016-11-23。

中央高校基本科研业务费专项资金(2016MS143)。

TP273；TP391

A

1672-0792(2017)02-0073-06

孙海蓉(1972-)，女，副教授，硕士生导师，研究方向为智能控制及其在工程中的应用、非线性控制，风力发电机组建模。

田瑶(1991-)，女，硕士研究生，研究方向为智能算法和优化控制。

谢碧霞(1992-)，女，硕士研究生，研究方向为智能算法和系统建模。

靳鑫(1994-)，女，大学本科，研究方向为智能算法和优化控制。