一种具有频率自适应能力的高精度数字积分算法

胡蔚中，杜 衡

(1. 三峡大学 电气与新能源学院，湖北宜昌443002； 2. 国网山西供电工程承装公司，山西太原030000)

一种具有频率自适应能力的高精度数字积分算法

胡蔚中1，杜 衡2

(1. 三峡大学 电气与新能源学院，湖北宜昌443002； 2. 国网山西供电工程承装公司，山西太原030000)

为增加空心线圈电子式电流互感器的工程实用性，必须解决其积分环节存在的误差与干扰问题。因此，在综合分析数字积分算法原理的基础上，以梯形积分算法为主体，结合FFT算法测量谐波频率的的功能，加入曲线拟合原理，设计出一种具有频率自适应能力的数字积分算法。根据谐波测量和电子式互感器校验系统的不同要求，提出算法的两种具体应用方案。仿真测试结果表明所设计算法展示出较好的性能：在电子式电流互感器的谐波信号测量中，可用多项式矫正各次谐波幅值误差，最终以12.8 kHz的采样速率使2～50次谐波电流信号计算出的幅值相对误差控制在0.01%以下。在电子式电流互感器校验系统中，以2 kHz的采样速率为例，该算法可有效抵抗电网信号频率±0.5 Hz波动的干扰，效果明显优于精度较高的辛普森算法。

谐波测量；数字积分器；梯形算法；电子式电流互感器；积分环节；曲线拟合

0 引言

在电力系统中，由于一些非线性用电设备的存在，使得公用电网中不可避免的存在谐波。谐波污染已经危害到电力系统本身，成为维护电力系统必须解决的重要问题之一，准确地检测谐波对谐波的抑制和治理有着重要的指导作用[1-4]。但是在公用电网中，被测电流和电压信号往往不能直接接入谐波测量仪器，需要通过电流互感器或电压互感器将它们调整到仪器可接收的范围，这就要求互感器具有准确的变比和良好的频率特性[5-7]。

如果选用空心线圈和模拟积分器组成的电子式电流互感器，在高压侧设计外积分电路，这个积分电路需要在2.5 kHz以内、温度变化的条件下稳定工作，对积分电容和积分电阻提出了极高的要求，设计难度较大[8-9]。如果选用数字积分器，利用传统的矩形、梯形、辛普森等积分算法，当被测信号为标准工频正弦信号且采样频率较高时，这些积分算法都可以达到相应的要求[10-11]。然而，当前的数字积分算法并不能实现对谐波信号的准确积分还原，也无法有效抵抗频率波动，在计算谐波信号时往往存在着较大的误差[12-14]。同时，低频小电流测量中电压漂移与噪声干扰问题是数字积分器难以应用于工程现场的重要原因。这无疑会影响后续的谐波准确提取和消除，进而影响电力系统的安全与稳定。虽然通过不断提高采样频率可以降低一定的误差，但也会同时增加对硬件的要求和运算量，增加电压漂移发生的可能性。因而需要特制高采样率的互感器，无法用常规互感器满足要求。

针对以上问题，本文设计了一种具有频率自适应能力的数字积分算法，可以在相对较低的采样频率下，将空心线圈电子式电流互感器积分环节中谐波幅值的比差降低到0.01%以下。同时，依据该算法设计了一种高精度数字积分器，使电子式电流互感器校验系统中在通用采样率时的积分环节误差大幅度降低，优于较为复杂的辛普森积分算法，有效避免了小电流测量中电压漂移和噪声干扰问题。

1 数字积分算法分析与改进

1.1 基本积分算法原理分析

如图1所示，常规梯形积分算法的基本几何原理是用梯形ABba的面积来等效曲边梯形ACBba的面积，进而通过重复累加求出整个积分区间的面积计算积分值。在实际工程中，提高采样频率相当于缩小步长即减小区间[a,b]，由图1可知，区间[a,b]越小梯形ABba的面积S1越接近于曲边梯形ACBba的面积S0。

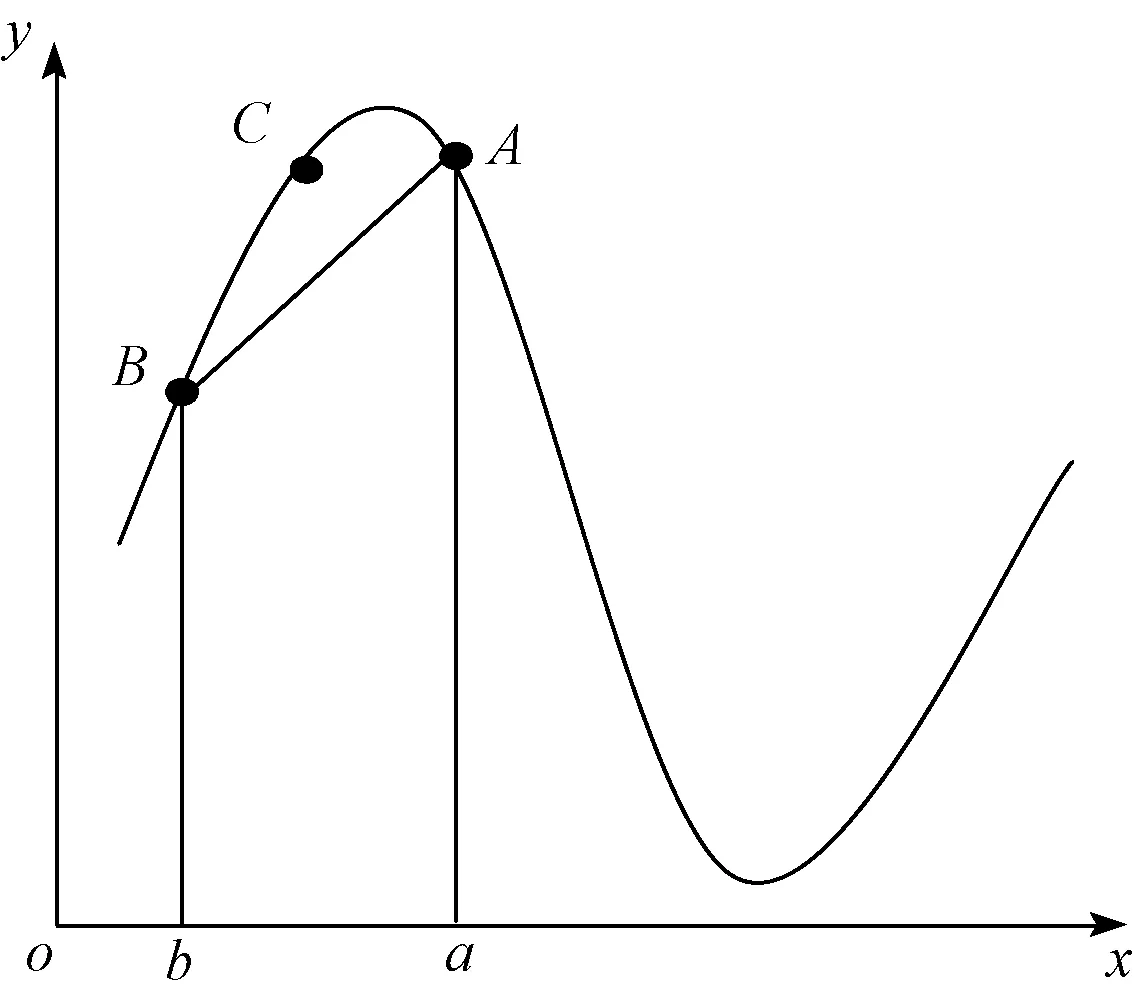
图1 梯形数字积分算法原理

基于该原理，为了降低空心线圈电子式电流互感器的误差，部分文献提出设计高运算量的传递函数或者增加数字积分器的采样频率[15-19]。然而，高采样频率同样会导致对于硬件的高要求和运算量的增加，也会提高对于算法频率跟踪能力的要求。同时，这些积分传递函数也无法避免数字角频率极小值处不收敛的共性。越是加倍采样频率，减小数字角频率，就会使传递函数越趋于零点，从而使电压漂移产生的可能性和低频噪声的危害性更大。

本文为了降低积分算法的误差，同时控制采样频率在一个合理的范围，提出在S0和S1之间引入一个调节系数Kxi，根据信号频率和采样频率等因素适当调整计算结果以降低误差，适当的采样频率也可有效降低电压漂移与低频噪声的影响。下面本文将具体分析Kxi的原理与设计过程。

1.2 数字域内梯形算法误差分析

传统的积分传递函数有复合矩形、梯形、辛普森公式等，其中梯形传递函数如下：

(1)

式中：T为采样间隔。由于传统积分算法的积分传递函数类似公式(1)属于不收敛的传递函数，所以当高采样频率下数字角频率处于极小值输入信号中含有直流信号或低频噪声时，传递函数幅值趋于无穷大，很容易导致承担数字积分硬件工作的微处理器很快溢出。另外，在数字域内有：

(2)

(3)

式中：N为单位周期内的采样点数；ωi为数字角频率。

(4)

综合式(3)、(4)可得出：

(5)

从该公式可知，第i次谐波信号的数字角频率ωi主要与第i次谐波信号的频率fi和采样频率fs有关。模拟理想积分器的传递函数为：

(6)

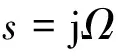
(7)

定义Ω为模拟角频率，则模拟角频率Ω与ωi之间的关系为：

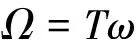
(8)

结合式(6)～(8)，得出梯形数字积分算法幅值绝对误差公式(9)，再结合公式(5)，可以得出E1(fi，fs)。绘制出幅值绝对误差E1(fi,fs)如图2所示。

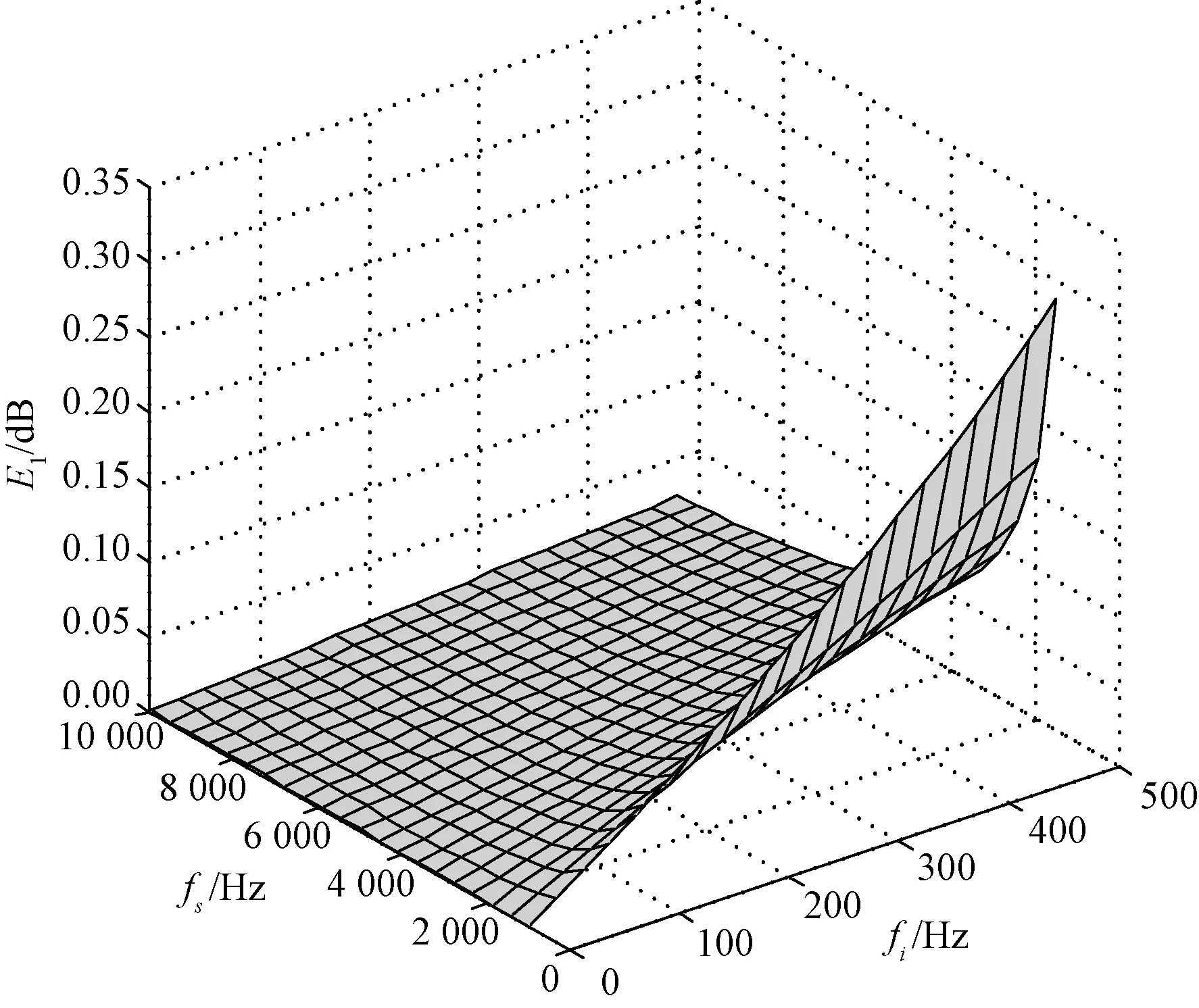
图2 梯形积分算法幅值绝对误差

其中，第i次谐波信号的频率fi取值范围在0～500 Hz，采样频率fs取值范围为0～10 kHz。

(9)

同样有梯形算法相位绝对误差公式(10)，结合公式(5)，可以绘制相位绝对误差E2(fi，fs)如图3所示。

(10)

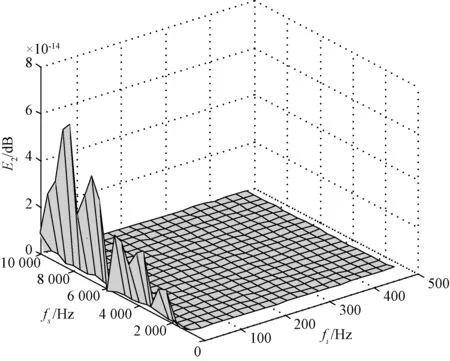
图3 梯形积分算法相位绝对误差

分析图1、2可知：梯形积分算法随着ωi的递增幅值误差迅速增加，而相位响应除了信号频率无限趋于零的极小值处有趋于无穷大的漂移外，整个频带基本上保持不变。因此，相位响应的极点也是在设计数字积分器时需要考虑的问题。

在工程中，用于保护的CT在IEC60044-8中只能做到最大每周期采样80点，根据前面所述，N越大，计算结果越精确，为了留有裕量，考察每周期内采样40点，即采样率为2 kHz。

设定采样频率2 kHz，比较梯形传递函数在不同信号频率下的幅值绝对误差，如图4所示。

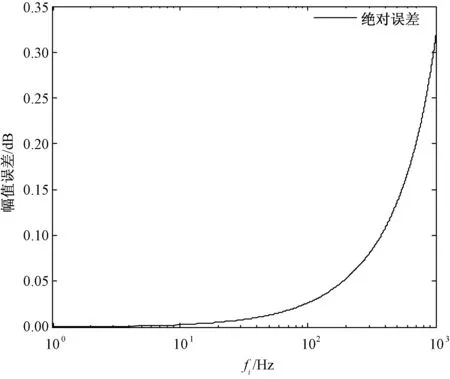
图4 固定采样频率下幅值绝对误差

由图4可知，在固定采样频率下，信号频率越小，幅值响应误差越小。由于数字积分算法的误差决定于采样频率与信号频率，由于在实际信号采集过程中采样频率通常设为定值，所以幅值响应误差仅与信号频率有关。

数字积分器的基本原理：在数字角频率ωi趋于零时矩形、梯形、辛普森公式的幅频特性与理想积分算法极为接近。然而事实上，结合图2与公式(1)可知，设计高采样频率的数字积分器虽然可以使其幅值误差无限趋于零，但也无限接近传递函数的极点，然而如果增加数字角频率以避免极点干扰，低采样频率通常无法满足幅值精度要求。

另外，在常见的工频信号中，当fs=2 kHz，f1=50 Hz，此时梯形算法幅值绝对误差E1≅0.013 dB。但是谐波频率随着谐波次数增加而递增，所以当谐波次数递增时幅值误差迅速增加，当信号为10次谐波f10=500 Hz时E1≅0.137 dB，这就是数字积分器测量工频信号和谐波信号不准确的重要因素。

I=sin(2πfit)

(11)

U=MdI/dt

(12)

在MATLAB M文件中编写fs=2 kHz的梯形数字积分程序，原始电流信号取公式(11)，微分信号按照公式(12)计算，为方便计算互感系数M取1，基波电流频率f1为50 Hz，逐次对2～10次谐波进行积分还原仿真实验，得出的相对误差如表1所示。

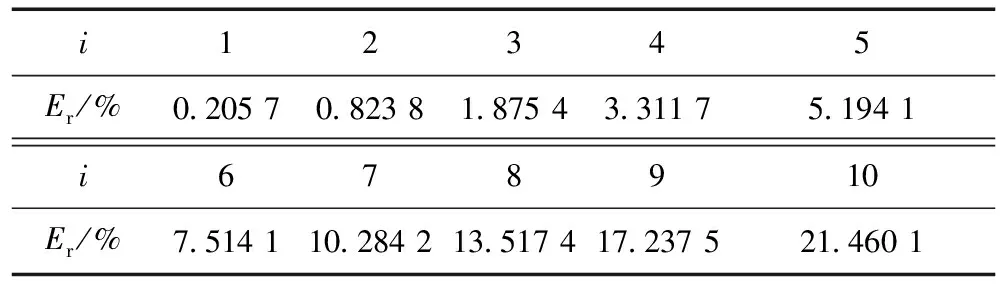
表1 各次谐波比差结果

在电子式电流互感器标准IEC60044-8规定中，不同准确级的电流互感器有各自不同精确度的要求，如：5p级的CT用于常规保护时，额定频率和谐波频率下比差分别小于1%和10%，相差小于±60′和10°。另外，根据《公用配电系统供电特性》和GB/T17626.7-2008规定：50次以下谐波相对误差不应超过5%。分析表1可知，在当前采样频率下，7次谐波以上梯形积分算法已经很难满足比差要求。

对于梯形积分算法，ωi越小幅值响应误差越小。由图3可知，除了极小值处的电压漂移外，在整个频带上梯形积分算法相位误差都极小，信号频率的变化对于相位响应的影响可以忽略不计，梯形算法这一优良特性是梯形、辛普森数字积分算法在设计空心线圈电子式电流互感器时得到应用的重要原因，因此本文在设计积分还原谐波的算法时仅考虑如何改善幅值响应与避免电压漂移。

1.3 积分算法改进措施与具体应用方案

1.3.1 积分算法改进措施

综合以上分析和结论，为降低梯形积分算法在第i次谐波信号测量中的误差，可以在梯形积分算法中引入第i次谐波的调节系数Kxi，从而根据信号频率实时调节幅频响应|HT(jωi)|，从而消除误差，具体见公式(13)、(14)。该调节系数可以避免相位响应和幅值响应处的极点，同时又合理消除幅值误差的基础。原理是采用低采样率增大数字角频率以避免极点的干扰，同时补偿因角频率增大产生的误差以保证精度，有效地降低了因零漂与噪声而产生微处理器溢出的可能性。

(13)

(14)

重复进行表1的仿真实验，使用加入调节系数后的数字积分程序，为在保证精度的前提下降低计算量，调节系数Kxi只取5位小数，如表2所示，实验结果如表3所示。

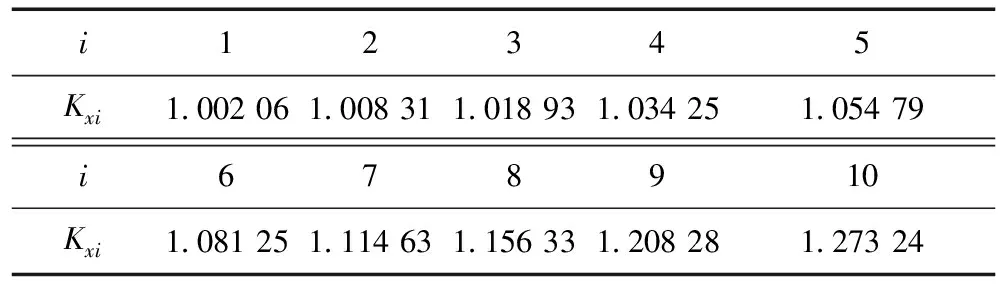
表2 不同谐波下调节系数表

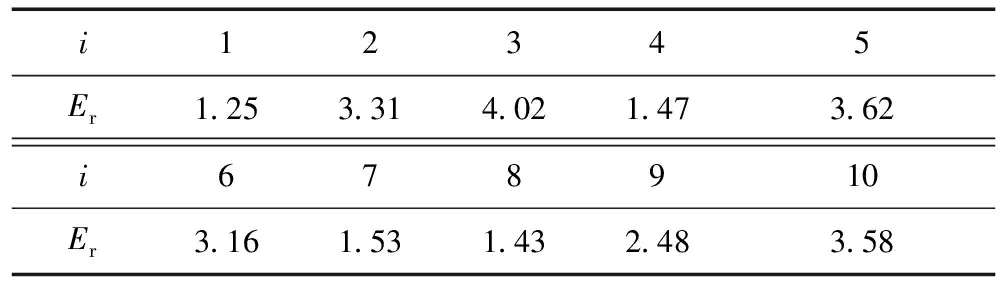
表3 改进后的谐波比差(Er/10-4%)

对比表1和表3可知，在引入调节系数后，2～10次谐波幅值误差大幅度降低，基本控制在10-3%以下。通常对于测量用电子式电流互感器而言，校验系统要求最高，为0.05级，即基频电流的幅值比差在额定电流时不超过0.05%，而谐波检测仪器的最高要求则是谐波相对误差不超过0.15%，所以这一误差已经满足所需精度要求，而且留有足够的裕量。如果有更高的精度需要，可以增加Kxi的小数位来提高准确度。

采样频率fs在积分环节中属于固定值，所以调节系数Kxi仅与第i次谐波的信号频率fi有关。由于模拟信号与数字信号的差异，在工程中很难直接调用公式(14)，所以下面提出一种使用曲线拟合的方法，设计出直接使用fi作为自变量的误差矫正函数。

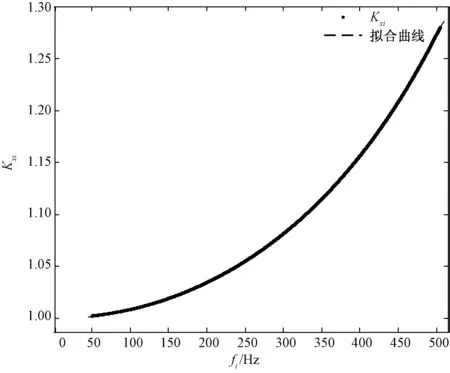
图5 调节系数Kxi拟合曲线

关于谐波信号频率的提取方法比较多，其中FFT(快速傅里叶)算法技术成熟，应用较多。当fs=2 kHz时，为了拟合基频到10次谐波的调节系数并使拟合公式更加准确，取信号频率范围10～550 Hz，步长0.01 Hz，绘制调节系数Kxi如图5所示，由于图像接近于多项式函数曲线，采用MATLAB CFTOOL工具箱进行曲线拟合。

多项式拟合后与公式(14)的方差对数随着多项式次数的增加而成线性规律减少，如图6所示。综合计算量和精度的要求，为测量50次以下谐波，在12.8 kHz采样率下，本文选用五次多项式作为矫正公式如式(15)。

Kxi(fi)=8.37×10-6fi4+9.007×10-16fi3-

1.331×10-12fi2+2.157×10-8fi+1

(15)

通过被采样信号的频率采集，使得调节系数可以同步进行调整，从而有效反馈给前端，最终使得输出信号可以最大程度上接近原始信号输出。在工程实际中，谐波测量设备和电子式电流互感器校验系统对于基波和谐波的测量要求不同，因此该算法的应用方案需要具体设置。此外，在工程中，通常在数字积分器添加前置信号调理电路，实现去噪、滤波等功能，以使输入信号的误差在可接受范围内。

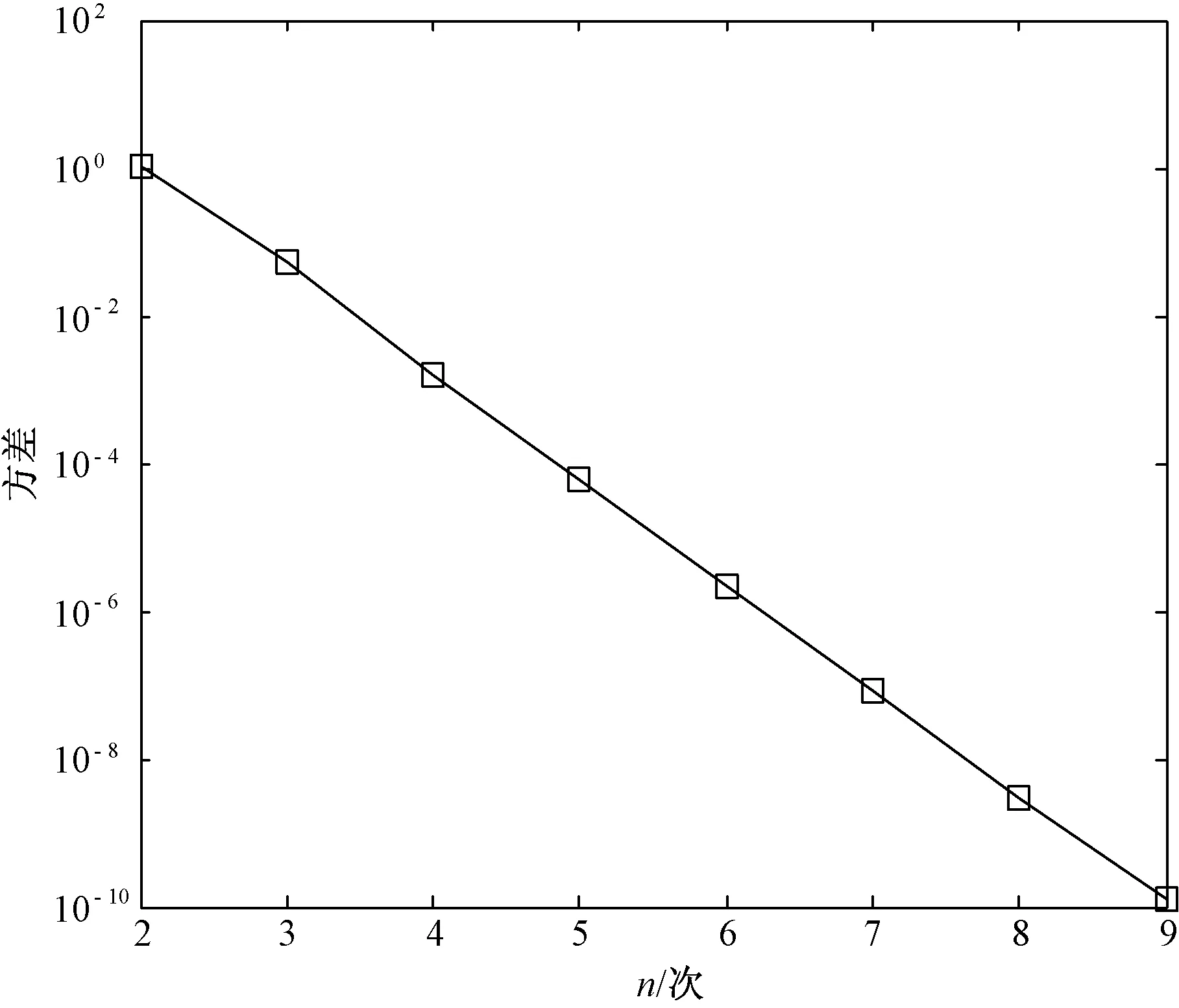
图6 拟合多项式方差变化

1.3.2 针对谐波测量的应用方案

在提取出各次谐波信号频率的基础上，也可以依据公式(16)直接调整各次谐波幅值有效值，也可以直接调整波形。

(16)

式中：Ii测为用FFT等谐波提取算法在积分还原后提取出的第i次谐波幅值大小；Ii实为第i次谐波实际幅值大小。该方法可以加入谐波提取算法流程中，用于直接修正最后结果，修正后结果如表4所示。因此，如果引入该调节系数，可以将各次谐波幅值的相对误差控制在0.01%以内。

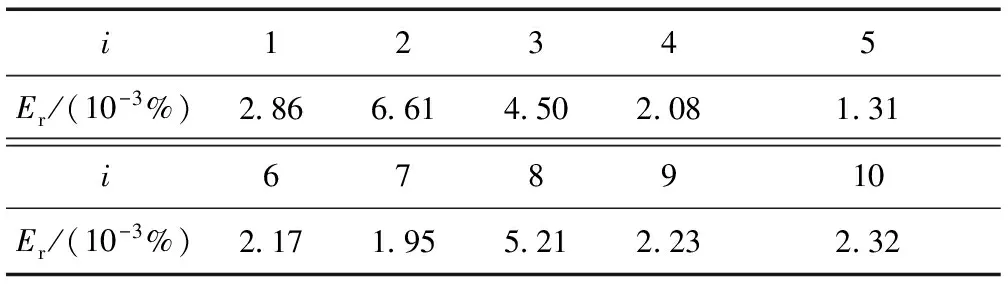
表4 拟合修正后的相对误差

为验证所设计的具有频率自适应能力的数字积分算法具有精确还原并提取谐波幅值的能力，对所设计的算法流程(如图7)在MATLAB M文件中进行检验与分析。其中，数字积分的传递函数仍采取传统梯形积分方案如公式(1)，仅在最后输出各次谐波幅值时用多项式函数(15)按公式(16)进行修正。

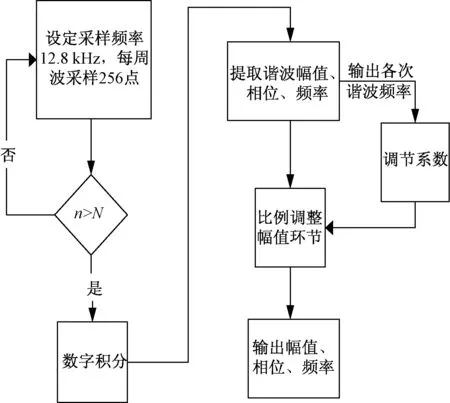
图7 软件流程图

1.3.3 针对校验系统的应用方案

针对电子式电流互感器的在线校验，目的是校准基波幅值与相位，极少关注高次谐波的准确性。因此仅以基波的调节系数作为积分环节的误差补偿方式，取信号频率波动范围49.5～50.5 Hz，步长取10-4Hz，拟合调节系数Kx1，由于Kx1曲线为一次函数，直接拟合一次函数公式：

(17)

该拟合公式与实际曲线的方差为4.06×10-13，相关系数为1，相对于公式(15)，采用公式(17)更为简单有效，因此，根据公式(13)设计出传递函数(18)。在梯形积分算法中引入该调节系数后，在测量基频电流时，所改进的算法与理想积分算法的误差基本可以予以消除，也可以有效抵抗频率小范围波动。

(18)

基于公式(18)设计的数字积分器结构如图8所示。前置高通滤波器用于消除模数转换器带来的直流干扰，积分环节仍旧采取传统积分方案如公式(1)，不同之处在于，FFT模块通过1周波的采样点提取基波信号频率，代入并求出调节系数Kx1进行调整。增加的模块可以有效抵抗信号频率小范围波动，提高空心线圈电子式电流互感器的性能。

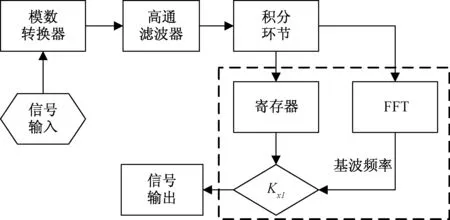
图8 数字积分器结构

2 积分算法仿真实验验证

2.1 谐波测量方案仿真测试

根据采样定理，要准确还原被测信号，采样频率至少是信号频率的2倍以上，要获取较高次谐波必须采用适当的采样频率，为测量算法对50次以下谐波测量效果，所以仿真实验采用测量用谐波测量中比较常见的12.8 kHz。为进行对比，同时用梯形积分算法进行测试。记录实验结果的幅值相对误差，测试结果记录如图9和图10所示。

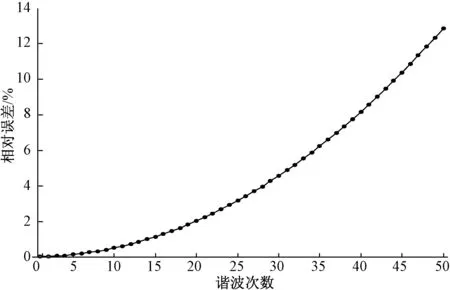
图9 梯形积分算法测试结果图

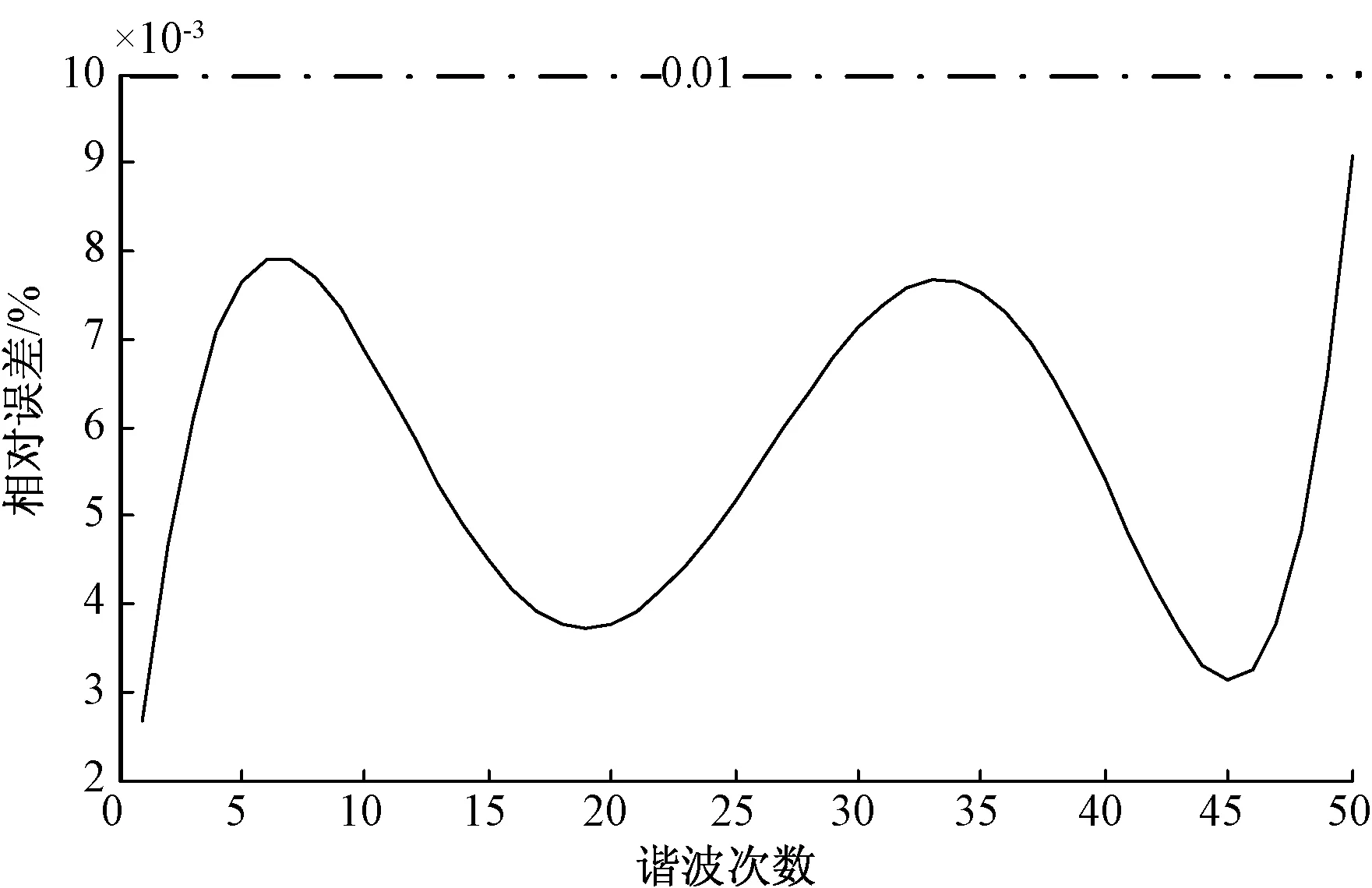
图10 矫正算法误差结果图

图10说明通过矫正误差，设计的谐波测量方案可以将测量谐波的误差降低到0.01%以下。实验结果显示，通过所设计的数字积分算法可以对50～2 500 Hz频段的谐波幅值进行准确测量，相对误差控制在0.01%以下，有效克服了原有梯形数字积分算法不适合于测量谐波幅值的缺点。

根据公式(14)绘制实际的调节系数如图11，可以发现，梯形积分算法的误差结果图9与所计算的实际的调节系数图11的曲线极为接近，这可以进一步证明：固定采样频率下，梯形积分算法的误差是成指数规律增长的。因此，所产生的误差可以通过多项式拟合予以补偿，这也从理论方面证明了实际改进措施是有效的。

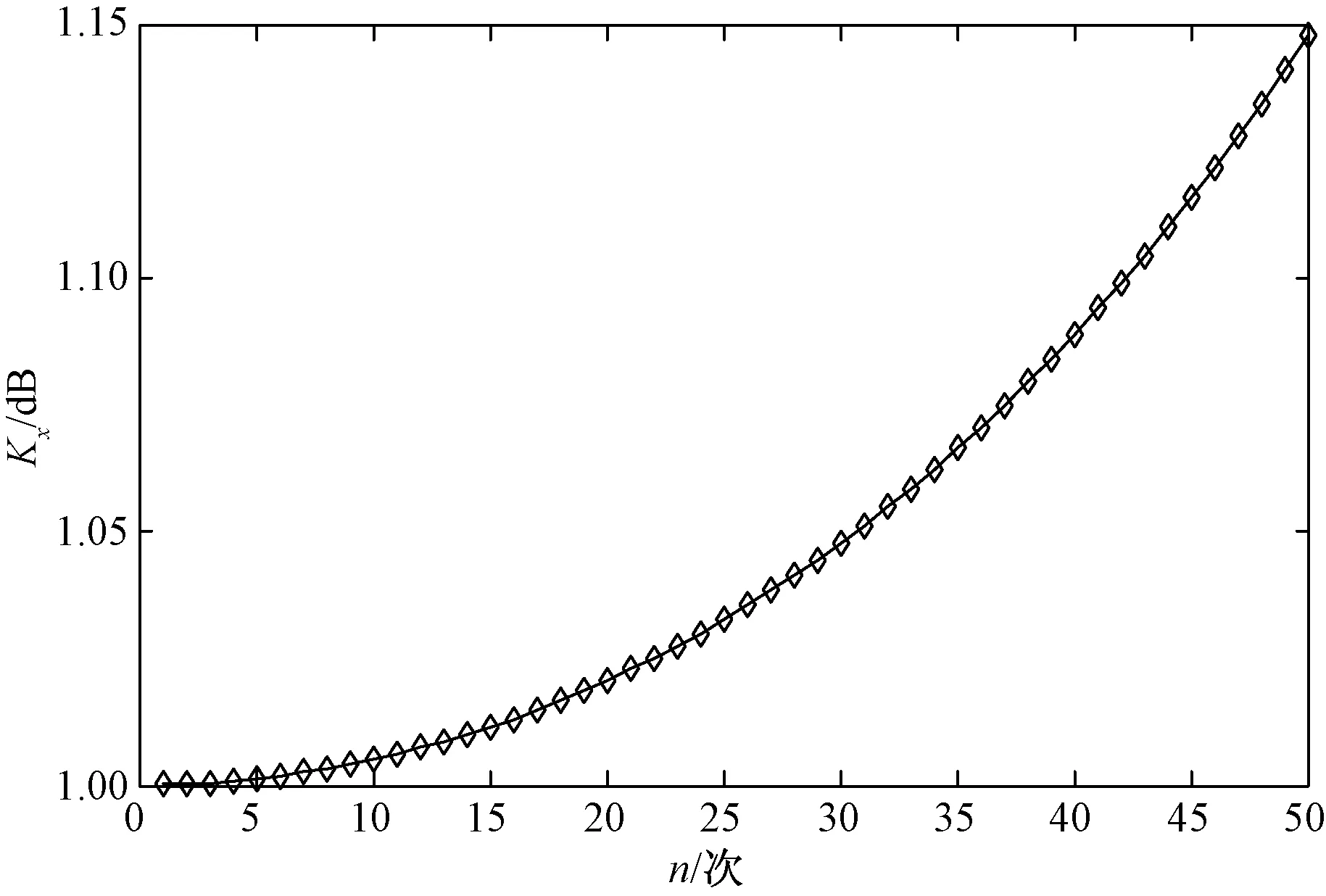
图11 调节系数曲线

2.2 校验系统方案仿真测试

在MATLAB M文件中编写程序进行仿真实验，继续取单位电流信号公式(11)按照公式(12)求微分信号进行测试。

为方便对比，选取具有较高精度的辛普森积分算法进行测试作为对照。同样将互感系数M取1，采样频率取2 kHz，信号频率取50 Hz，将微分信号分别按照辛普森积分算法和改进后的积分算法进行计算，求出还原信号与原始信号的误差E，结果如图12所示。

(19)

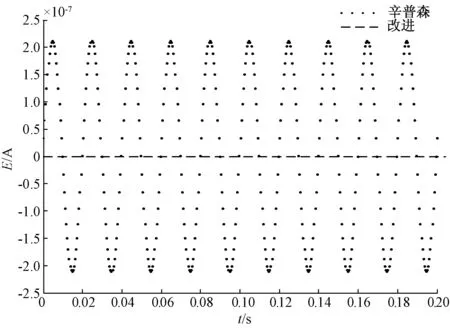
图12 测试结果对比

仿真实验结果表明：相对于同样采样频率的辛普森积分算法，所设计的数字积分算法对于工频信号具有更小的误差。取信号频率49.5～50.5 Hz，再次用所设计的方案如图8对电流微分信号做测试，记录误差E，结果如图13所示。

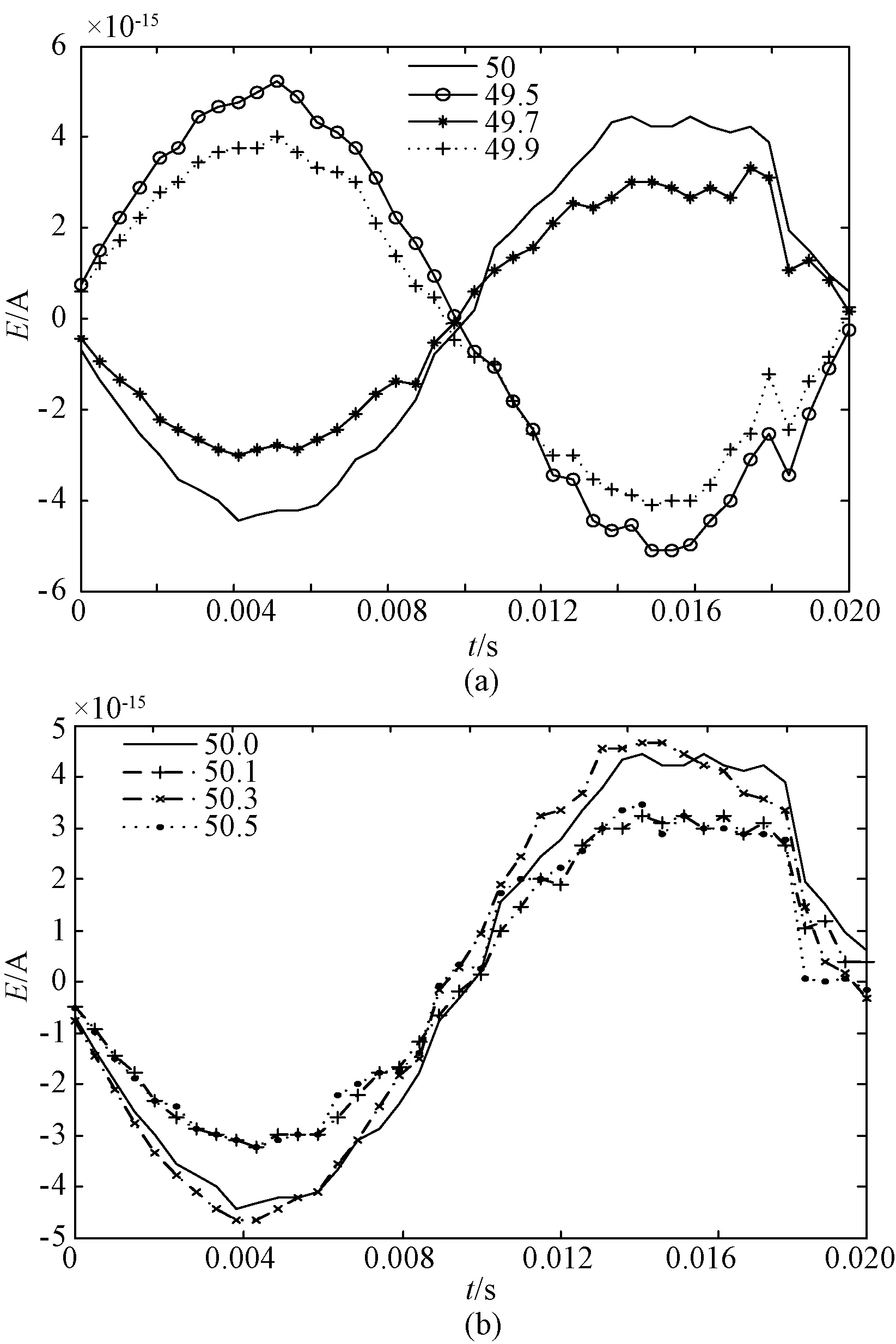
图13 频率小范围波动时误差对比

由图13可见，所设计的方案不受小范围频率波动的影响，由于频率波动所产生的幅值误差基本可以忽略不计。

3 结论

本文针对谐波测量仪器接入公用电网需要互感器作为测量前端，而常用的空心线圈电子式电流互感器无法准确测量谐波，数字积分器因采样率不足幅值误差较大的问题进行了研究。根据固定频率下数字积分算法误差呈指数规律的原理，本文设计了一种具有频率自适应的数字积分算法，以12.8 kHz的采样频率，实现了频率范围在50～2 500 Hz的谐波信号幅值准确测量，相对误差小于0.01%，足以满足日常测量需要。另外，依据该算法设计了一种数字积分器，可以选择通用的采样率以降低电压漂移出现的可能性，采样点的减少同样会减少干扰噪声的引入，调节系数的设计又补偿了采样率不足带来的误差，保证了测量精度。

[1]俞志勇，李青，王燕杰，等. 基于PID的流量调节阀的设计[J]. 计算机测量与控制, 2016, 24(8):118-121.

[2]张杰，胡媛媛，刘飞，等.高压直流互感器现场校验关键技术[J].高电压技术，2016，42(9)：3003-3010.

[3]宋璇坤，闫培丽，肖智宏，等.全光纤电流互感器技术应用评述[J]. 电力系统保护与控制，2016，44(8)：149-154.

[4]程妮. 提高数字化变电站继电保护系统可靠性措施分析[J].电子世界，2016(8)：138-139.

[5]石建华.方形截面Rogowski线圈的一致性分析[J].电测与仪表，2016，53(7)：124-128.

[6]何瑞文，蔡泽祥，王 奕，等.Rogowski线圈电流互感器传变特性及其对继电保护的适应性分析[J].电网技术，2013，37(5)： 1471-1476.

[7]冯宇，万罡，舒开旗，等.电流互感器暂态特性试验用标准信号的参数估计[J].电网技术，2014，38(8)：2263-2267.

[8]卢嘉栋.电流互感器在线校验关键技术论述[J].电子技术与软件工程，2016(13)：142-143.

[9]李远松，高博，丁津津，等.特高压保护用电流互感器励磁特性现场测试[J].变压器，2016，53(7)：73-76.

[10]ALAOUI A，MOHAMAD A.Class of digital integrators and differentiators[J].IET Signal Processing，2011，5(2)：251-260.

[11]NGO N Q. A new approach for the design of wideband digital integrator and differentiator[J].Circuit & System//Express Briefs IEEE Transactions on,2006，53(9)：2300-2309

[12]王玮，徐丙垠，王华广，等.基于光强调制原理的电流互感器设计方法[J].高压电器，2016，42(7)：61-67.

[13]王建华，张国钢，耿英三，等.智能电器最新技术研究及应用发展前景[J].电工技术学报，2015，30(9)：1-11.

[14]邱鑫茂，马靖，谢楠，等.适用于任意电场分布和传播方向的电光器件仿真方法[J].光学学报，2015，12(11)：248-255.

[15]宋涛.Rogowski线圈电流互感器中的高精度数字积分器技术研究[J].高电压技术，2015，41(1)：237-244.

[16]张可畏，王宁，段雄英，等.用于电子式电流互感器的数字积分器[J].中国电机工程学报，2004，24(12)：104-107.

[17]TSENG C C.Design of digital Feller fractional order integrator [J].Signal Processing，2014，102：16-31.

[18]吴超凡，陈隆道.基于分段插值同步化算法的谐波测量[J].电力系统保护与控制，2016，44(9)：1-6.

[19]钟丹田，韩芳，刘齐，等.高压电缆终端避雷器带电检测系统研制[J].电气应用，2015(S2)：237-241.

A High Precision Digital Integrator Algorithm with Frequency Self-adaption Ability

HU Weizhong1, DU Heng2

(1. College of Electrical Engineering and New Energy, Three Gorges University, Yichang 443002, China;2. Power Supply Engineering of Shanxi State Grid Corporation, Taiyuan 030000, China)

In order to promote the practical usage of the Rogowski coil electronic current transformer in the harmonic signal measurement, the error problem in the integral part is considered to be essential and urgent to be solved. Therefore, on the basis of comprehensive analysis of the digital integral algorithm, a new digital algorithm with the frequency self-adaption ability is designed in this paper. Combining the principle of curve fitting with FFT algorithm used for measuring signal frequency, the algorithm is designed. The improved algorithm could integrate the differential signal of 2～50 order harmonic component measurement precisely at the sampling frequency 12.8 kHz. The relative error of numerical integral link could be controlled below 0.01%. Finally, an electronic current transformer with frequency compensation ability is designed according to the proposed algorithm. It is effective for resisting the ±0.5 Hz frequency fluctuations and can reduce the noise error.

harmonic measurement; digital integrator; trapezoidal algorithm; electronic current transformer; integral link; curve fitting

10.3969/j.ISSN.1672-0792.2017.02.001

2016-08-18。

三峡大学2016年硕士学位论文培优基金(2016PY041)。

TM452

A

1672-0792(2017)02-0001-08

胡蔚中(1990-),男,硕士研究生,研究方向为数字化变电站设备状态监测技术。