基于递推最小二乘算法的逆变器参数辨识

张海宁

(青海省光伏并网发电技术重点实验室，青海西宁810000)

基于递推最小二乘算法的逆变器参数辨识

张海宁

(青海省光伏并网发电技术重点实验室，青海西宁810000)

逆变器作为光伏发电并网系统的关键元件，其性能不仅影响和决定整个光伏并网系统是否能够稳定、安全、可靠、高效地运行，同时也是影响整个系统使用寿命的主要因素。针对现阶段已有的逆变器模型及控制系统研究的不足，采用电压型三相桥式逆变电路的结构，电压外环、电流内环的双闭环控制，并推导出了逆变器的dq轴解耦待辨识模型，采用递推最小二乘算法对该模型进行参数辨识，得到了各个待辨识参数的实际值，由辨识结果可以看出辨识误差较小，辨识值与设定值非常接近，并在模型中加入了扰动实验，进一步验证了该算法在逆变器辨识方面的准确性和可行性。

逆变器；参数辨识；dq轴参数解耦；递推最小二乘算法

0 引言

随着新能源、微电网技术和智能电网的快速发展，光伏发电系统已经得到比较广泛的应用，并具有广阔的发展前景[1]。并网光伏发电系统通过逆变器接入电力系统，逆变器作为能量转换单元提供必要控制，已成为光伏发电系统的核心单元[2]。光伏阵列输出的直流电由逆变器转换为满足电网要求的交流电，再输入电网的设备，逆变器的性能不仅影响和决定整个系统的安全性、高效性、稳定性及可靠性，同时也能直接影响整个系统的使用寿命[3]。

光伏并网逆变器根据有无隔离变压器可分为隔离型和非隔离型，其中，隔离型逆变器可分为高频和工频逆变器，非隔离型逆变器可分为单级和多级逆变器。其控制方式有多种，如 PQ 控制、v/f 控制、斜率控制等。一般逆变器控制采取电压外环和电流内环的双闭环控制，电压外环、电流内环多采用PI控制器来进行调节，但仅通过常规的PI控制很难对正弦电流达到理想的控制，通常还加入比例-谐振控制设计环节，减少谐波输出，完成直流电压的无静差控制[4]。目前，国内外关于光伏逆变器的模型及参数辨识方法的研究并不太成熟，研究成果也相对较少。文献[2]2440利用非线性系统辨识技术，建立了并网逆变器的模型，并将逆变器当做“黑箱子”，根据“黑箱子”的输入输出，对逆变器进行辨识；文献[5]基于实测数据，搭建了并网光伏发电系统逆变器的模型，并提出了针对典型光伏并网逆变器双环控制模型的dq轴参数解耦辨识策略，但文章对于参数辨识过程缺乏详细的阐述；文献[6]搭建了整个光伏系统的模型，并采用递推最小二乘算法对光伏系统进行了参数辨识，但对于逆变器控制模型及该算法在逆变器参数辨识领域应用意义的相关描述较少；文献[7]提出了光伏逆变器的Wiener 模型，并验证了Wiener 模型在不同光照强度下的稳态特性；文献[8-9]采用了最小二乘法辨识了并网光伏发电系统仿真模型的参数。

在以往的参数辨识过程中，国内有学者通过考虑配电网网侧接入光伏发电系统后对综合负荷模型的影响，建立了整个并网光伏发电系统的模型，并通过建模过程推导计算出了整个系统的外特性方程，但该学者在建立的并网光伏发电系统模型时，并没有考虑电流内环的控制，因此，在多次的扰动辨识实验中，并网逆变器电压外环控制的参数辨识结果也有较差的一致性[10]。针对并网光伏逆变器的控制模型的参数辨识，通常直接调节逆变器的输入，设置一次侧电压和无功的跳变来引发设备的动作，或者在PI控制器参数的参考值上制造阶跃扰动。但内环控制器与外环控制器之间相互关联，相互影响，想要在同一扰动下既辨识内环参数，又辨识外环参数的难度很大，辨识结果通常表现为，动态响应曲线有较好的拟合水平，但运用算法进行优化辨识时，参数的多次辨识结果有很大差异[11]。

针对上述不足，本文采用典型光伏逆变器拓扑结构，即电压型三相桥式逆变电路的结构，控制系统采用电压外环、电流内环的双闭环控制，通过对原始方程的简化及计算，得到解耦的并网逆变控制器dq轴参数方程，从而建立待辨识的dq轴解耦模型；并采用递推最小二乘算法对待辨识模型进行参数辨识，该算法方法具有算法简单、计算量小，稳定性强，多次辨识的结果相差小，一致性高，通用性强，可实时在线辨识的优势，在逆变器模型辨识过程中得到了更为准确的逆变器控制参数。

1 并网光伏逆变器模型及其控制策略

1.1 逆变器模型

并网光伏发电系统主要由光伏阵列、DC-DC变换器、DC-AC逆变器和控制系统组成。光伏阵列实现将太阳的辐射转化为直流电能；DC-DC为Boost升压电路，实现转换前后电压、电流不同的直流电、直流电之间的转换功能，即将光伏阵列输出的直流电压转换为可输入逆变器的直流形式，调整光伏阵列的输出电压到一个合适的值以配合电网电压的大小，同时实现光伏电池输出最大功率点跟踪(MPPT)，使光伏模块稳定地工作在最大功率点；逆变器实现将太阳能发电系统所发出的直流电转换为与电网同频率、同相位的交流电的功能，是连接光伏模块和电网至为关键的一环。

逆变器由IGBT等功率开关器件构成，控制电路使开关元件有一定规律的连续开通或关断，使输出电压极性正负交替，将直流输入转换为交流输出。本文采用典型光伏逆变器拓扑结构，即电压型三相桥式逆变电路，其结构如图1所示。

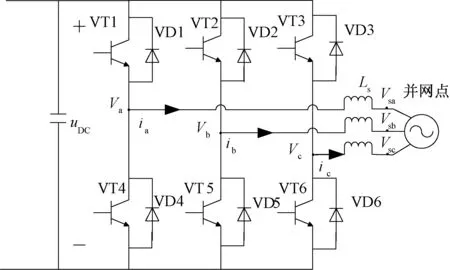
图1 电压型三相桥式逆变电路结构图

其中，VT1 VT6、VD1 VD6 为 IGBT开关管；uDC为直流侧电压；Va、Vb、Vc为三相电压源换流器交流侧电压；Vsa、Vsb、Vsc为并网点电压；ia、ib和ic为逆变器输出电流。

1.2dq轴解耦的辨识模型

光伏逆变器一般采用电压外环、电流内环控制的双闭环控制结构。在同步旋转参考坐标系下，电压外环是将直流电压和逆变器输出的无功功率分别与参考信号进行比较，得到的误差信号经过PI控制器后，其输出分别为电流内环的参考值Id_ref和Iq_ref；内环电流控制器采用PI控制器，其输出与交叉解耦项之和等于逆变器输出电压。内环电流控制、外环直流电压/无功功率控制方程及滤波器电路方程分别如式(1)、(2)、(3)所示。

(1)

(2)

(3)

式中：Vd和Vq分别为逆变器输出电压的d轴和q轴分量；Ls为滤波电感；Vsd、Vsq分别为并网点电压的d轴和q轴分量；Id，Iq分别为逆变器输出电流的d轴和q轴分量；Id_ref和Iq_ref分别为由外环输出的内环电流dq轴参考值；kPI1和kII1分别为内环d轴电流控制器的比例和积分系数；kPI2和kII2分别为内环电流q轴控制器的比例和积分系数；ω为锁相环输出的当前系统频率。UDC_ref为直流侧电压参考值，；kPU和kIU分别为电压外环控制器的比例和积分系数；kPQ和kIQ分别为无功功率控制器的比例和积分系数；Q为无功功率测量值；Qref为调度给定的无功功率参考值，本文设置为0。逆变器控制方程(1)中存在dq轴的耦合项，辨识难度大。为减少方程中变量的个数，结合式(1)、(3)，可得:

(4)

将式(2)代入式(4)，整理可得不含耦合项的辨识方程如式(5)、(6)所示:

(5)

(6)

式(5)、(6)实现了dq轴参数解耦。根据式(5)、(6)得到待辨识的参数为kPI1,kII1,kPU,kIU,Ls,kPI2,kII2,kPQ,kIQ。基于光伏发电系统模型与逆变器dq轴解耦模型的系统辨识框图如图2所示。

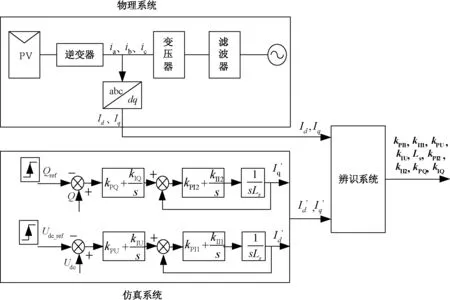
图2 系统辨识框图

2 基于递推最小二乘算法的逆变器模型辨识

在研究系统辨识问题时，常把待辨识系统进行“黑箱”处理，即不考虑内部结构，只考虑系统的输入-输出特性。系统辨识中，最小二乘法作为一种最基本的算法，得到了广泛的应用，其包括非递推最小二乘法和递推最小二乘法2种形式。本文采用递推最小二乘辨识方法，对式(5)、(6)的模型中的9个参数进行递推估计。该算法方法简单、计算量小，稳定性强，多次辨识的结果相差小，一致性高，通用性强，可实时在线辨识[12]。

先对d轴未知参数进行辨识，d轴辨识模型的输出变量为Id，需要辨识的参数为kPI1,kII1,kPU,kIU,Ls。之后固定Ls和d轴辨识的结果，继续辨识q轴参数kPI2,kII2,kPQ,kIQ。由于dq轴解耦后需要辨识的模型是一个非线性方程，首先要将其线性化为递推最小二乘算法的模型形式，具体线性化方法见文献[13]。设定目标函数为：

(7)

式中：Ys为实际系统的观测值，即Id与Iq的实测值；Yj为由仿真模型计算得出的逆变器dq轴输出电流组成的矩阵。递推最小二乘算法步骤如下：

考虑典型差分方程模型：

(8)

且定义向量

(9)

(10)

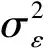
(11)

定义

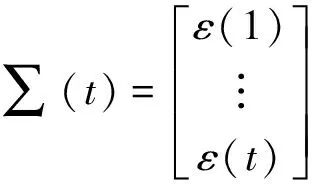
(12)

可将它们合写为矩阵向量形式：

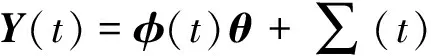
(13)

定义n×n矩阵

(14)

则由推导可得到RLS模型的参数估值为：

(15)

(16)

(17)

表1 模型参数辨识结果

式中：θ(t)为待辨识的参数向量；F(k)为增益矩阵；φ(t+1)为观测矩阵；P(t)为协方差矩阵。图3为程序流程图。

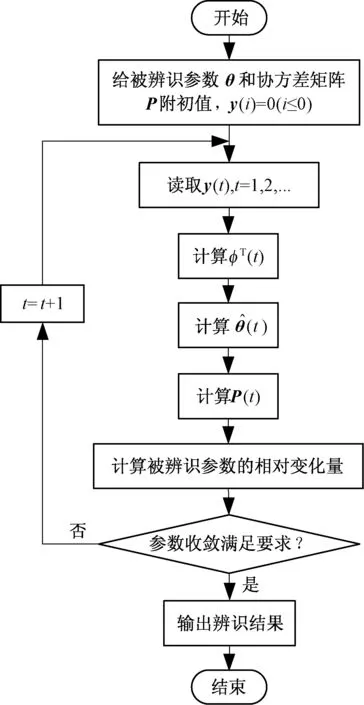
图3 递推最小二乘算法程序流程图

3 辨识结果及分析

为了验证递推最小二乘算法在逆变器参数辨识领域的准确性及有效性，利用MATLAB软件搭建了逆变器dq轴解耦的辨识模型及整个光伏发电系统的模型，并根据以往运行经验给出了各个控制参数的一组设定值，如表1中所示。测试数据为经过滤波电感后的dq轴电流值Id、Iq。

本文采用递推最小二乘算法对未知参数进行辨识，将Id的实测值作为递推最小二乘模型的输入量，辨识参数kPI1,kII1,kPU,kIU,Ls。随后，固定Ls和d轴辨识的结果，将Iq的实测值作为递推最小二乘模型的输入量，继续辨识q轴参数kPI2,kII2,kPQ,kIQ。由于在逆变器控制系统中，kPU,kIU的取值分别与kPQ,kIQ的取值相同，因此只需继续辨识kPI2,kII22个参数。迭代次数取500次，迭代过程中各参数的变化趋势及辨识结果分别如图4～10所示，可以看出，随着迭代次数的逐渐增加，9个参数分别逐渐稳定在某一定值附近。各个参数的辨识值与设定值对比见表1，残差平方和J如图11所示，可以看出仿真误差较小，算法精度较高。

图4 kPI1辨识过程曲线

图5 kII1辨识过程曲线

图6 kPU辨识过程曲线

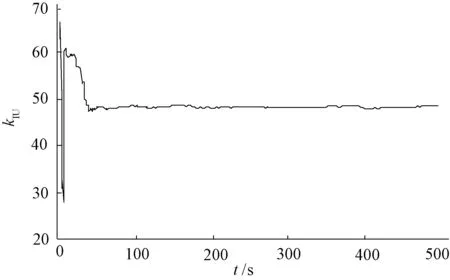
图7 kIU辨识过程曲线

图8 Ls辨识过程曲线

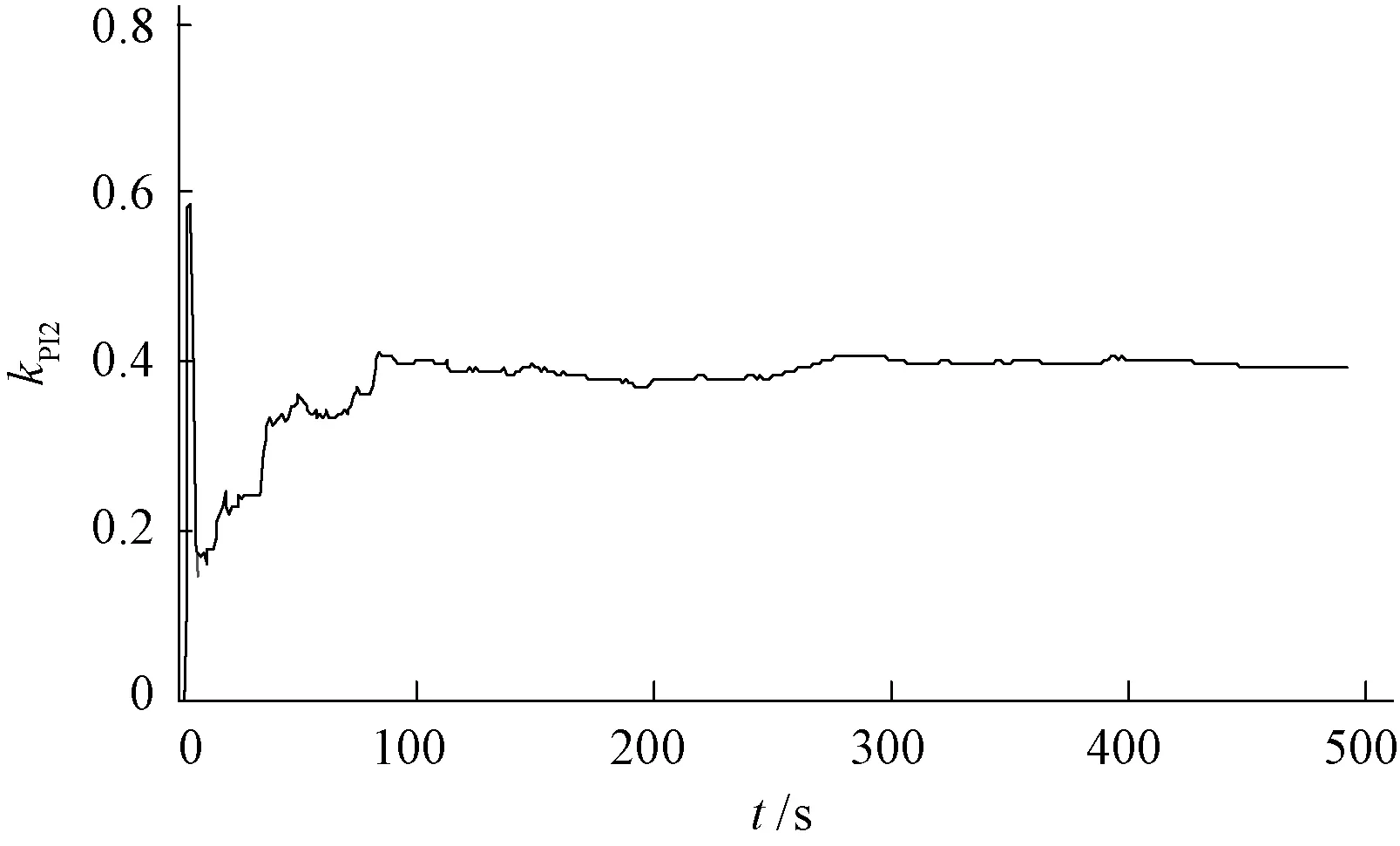
图9 kPI2辨识过程曲线

图10 kII2辨识过程曲线

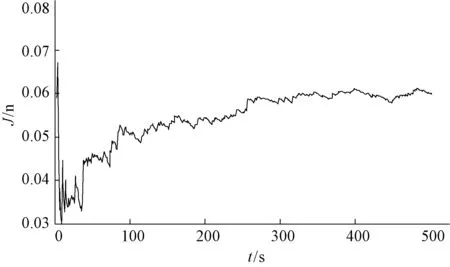
图11 残差平方和(RSS)J过程曲线

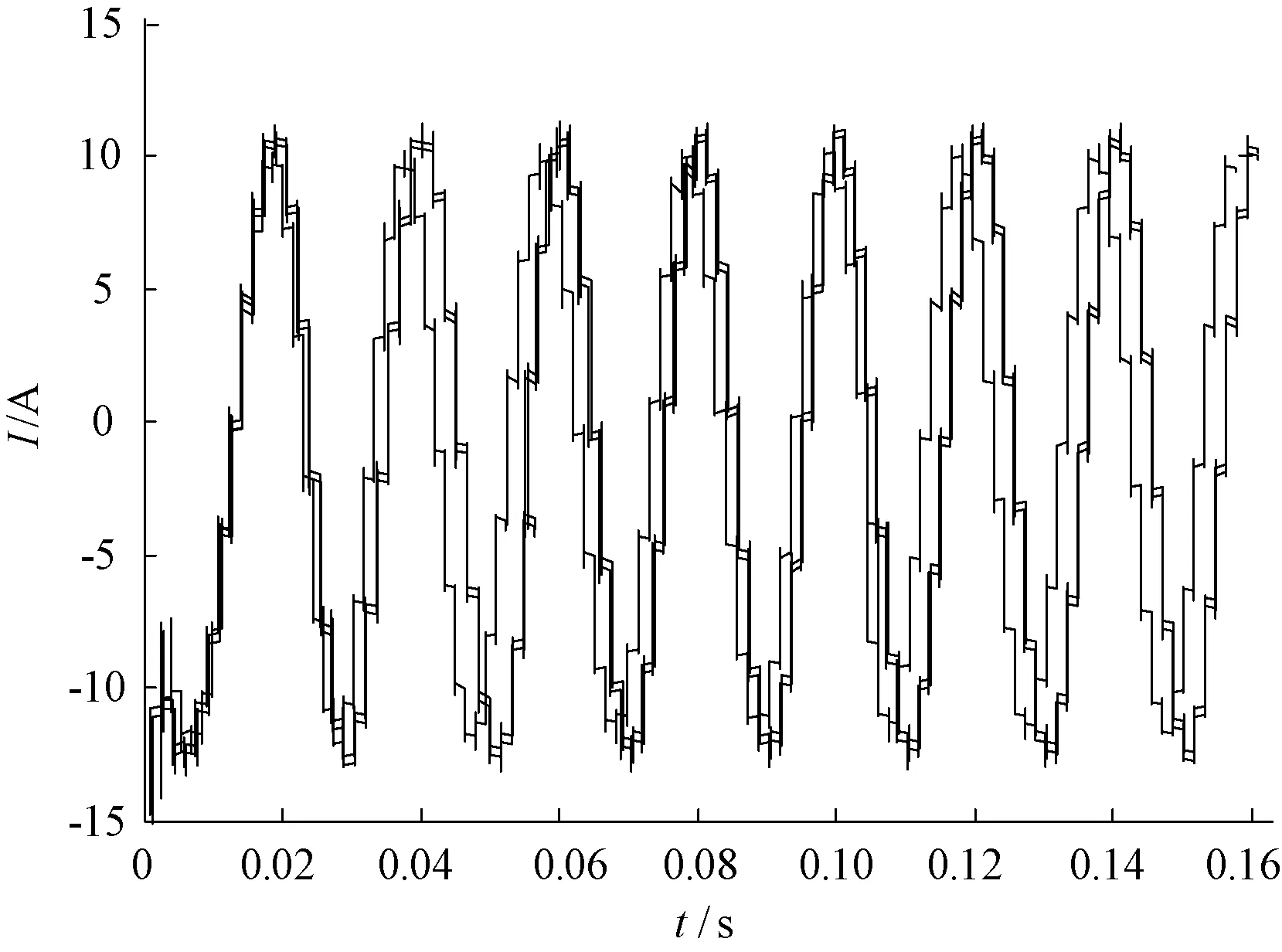
图12 逆变器输出波形

图12为光伏发电系统单相输出曲线，其中，基于设定值的输出曲线如图中虚线所示，实测曲线如图中点化线所示，由两条曲线对比可以看出，实测曲线与基于设定值的仿真曲线之间有很大的偏差；辨识曲线如图中实线所示，可以看出，辨识曲线与实测曲线有较好的一致性，进一步验证了该算法在逆变器辨识方面的准确性和可行性。

以上辨识过程基于稳态运行时的仿真模型，光伏阵列稳定地运行在最大功率点，现在MATLAB搭建的模型中设置如下扰动：Udc_ref(标幺值)在0.2 s时发生20%的跳变，Qref在0.3 s时发生从0～0.3(标幺值)的跳变，并记录基于控制系统参数设定值、辨识值、实测数据的光伏发电系统的输出曲线如图13所示。图中，长虚线为基于设定参数值的光伏逆变器输出结果，实线为根据实测数据画出的输出曲线，点化线为辨识曲线。由图中可以看出，在加入扰动后，实测曲线与基于设定值的输出曲线之前有较大偏差,而基于辨识值的逆变器输出特性曲线与基于实测数据的逆变器输出特性曲线拟合程度依然很高，该辨识方法的辨识精度仍能得以满足。

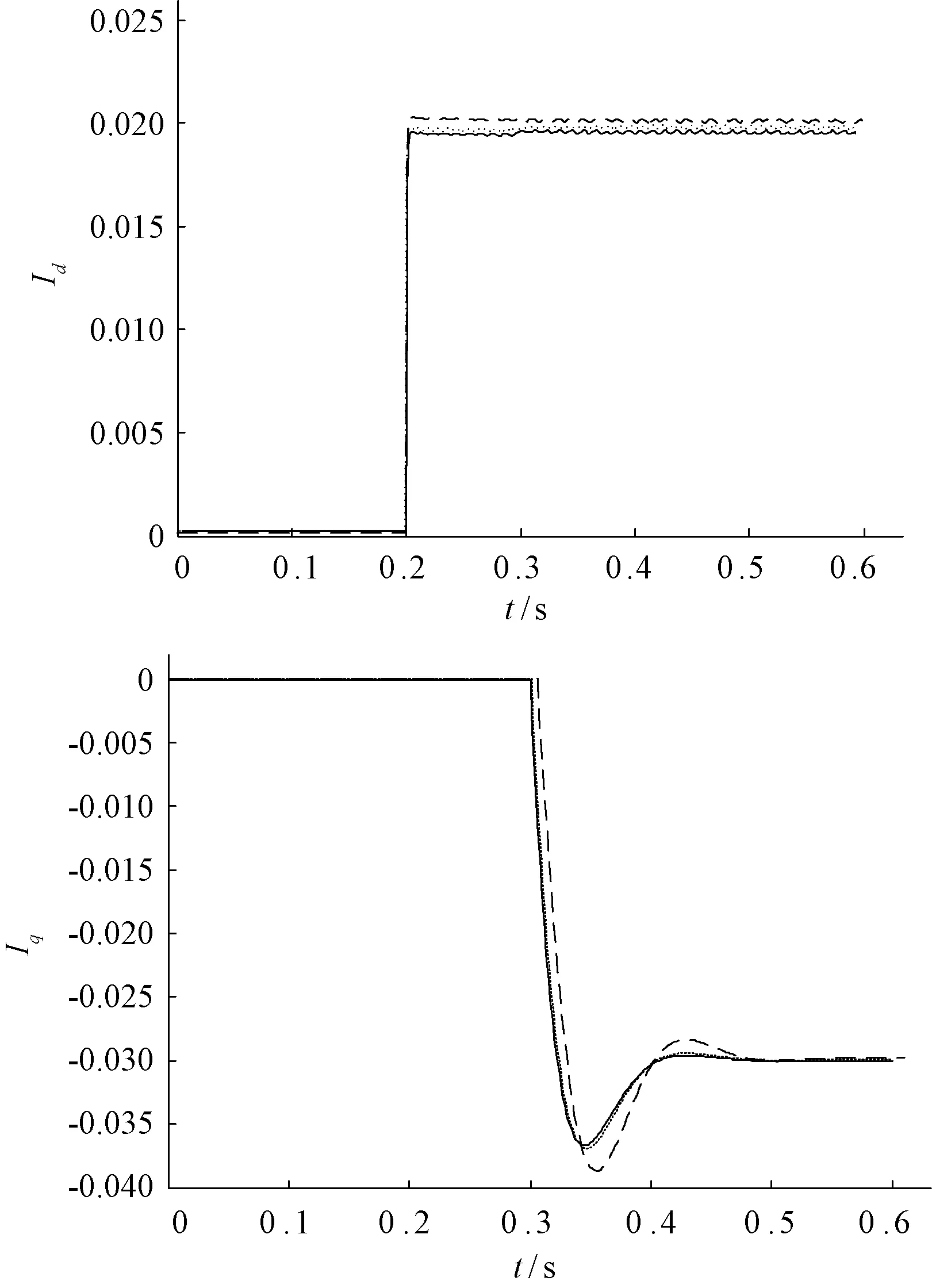
图13 dq轴电流对比曲线

4 结论

光伏并网逆变器是光伏系统的核心装置，对其模型及控制系统进行参数辨识研究具有重大意义。本文采用了电压型三相桥式逆变电路的结构，建立了并网逆变器的模型，并采用电压外环、电流内环的双闭环控制系统，建立了逆变控制器dq轴参数解耦模型；采用递推最小二乘算法对待辨识模型进行参数辨识，该方法算法简单、计算量小，稳定性强，多次辨识的结果相差小，一致性高，通用性强，可实时在线辨识。由仿真结果可以看出仿真误差较小，辨识值与理论值非常接近，在加入扰动后，拟合效果仍然较好，验证了该算法在逆变器辨识方面的准确性和可行性，得到更为准确的逆变器控制参数，为光伏逆变器参数辨识提供了一个准确可行的方法。

[1]孙浩,张曼,陈志刚，等. 并网光伏发电系统的通用性机电暂态模型及其与电磁暂态模型的对比分析[J]. 电力系统保护与控制，2014，42(3)：128-133.

[2]郑伟,熊小伏. 光伏并网逆变器NARX模型的系统辨识[J]. 电网技术，2013，39(9)：2440-2445.

[3]张兴，曹仁贤. 太阳能光伏并网发电及其逆变控制[M]. 北京：机械工业出版社，2010.

[4]王皓怀，汤涌，侯俊贤，等.风光储联合发电系统的组合建模与等值[J].中国电机工程学报，2011，31(34)：1-9.

[5]沈欣炜,郑竞宏,朱守真，等. 光伏并网逆变器控制参数的dq轴解耦辨识策略[J]. 电力系统自动化，2014，38(4)：38-43.

[6]付兵彬，贾春蓉，杨昌海，等.光伏并网发电系统仿真模型的参数辨识[J].电力系统及其自动化学报，2013，25(5)：116-120.

[7]郑伟，熊小伏.基于 Wiener 模型的光伏并网逆变器模型辨识方法[J].中国电机工程学报，2013，33(36)：18-26.

[8]熊小伏，陈康，郑伟，等.基于最小二乘法的光伏逆变器模型辨识[J].电力系统保护与控制，2012，40(22)：52-57，63.

[9]郑伟. 光伏并网逆变器辨识建模方法及应用[D].重庆：重庆大学，2014.

[10]张剑，孙元章.三相单级光伏并网系统对配电网侧负荷建模的影响[J].电力系统自动化，2011,35(2):73-78.

[11]金宇清,鞠平,潘学萍,等. 光伏逆变器控制参数的分步辨识方法[J]. 电网技术，2015，39(3)：594-600.

[12]赵海森,杜中兰,刘晓芳,等. 基于递推最小二乘法与模型参考自适应法的鼠笼式异步电机转子电阻在线辨识方法[J]. 中国电机工程学报，2014，34(30)：5386-5394.

[13]潘月斗,陈继义,徐杰，等.矩阵变换器输入电流的状态反馈线性化控制[J].高电压技术，2014，40(8)：2497-2503.

《电力科学与工程 》

欢迎投稿

欢迎订阅

投稿网址：http://www.dlkxygc.com

Parameter Identification of Inverter Based on Recursive Least Square Algorithm

ZHANG Haining

(Qinghai Province Key Laboratory of PV Grid Connected Power Generation Technology, Xining 810000，China )

As a key component of PV grid connected system, not only the stability, security, reliability and efficiency of the whole PV system are affected by the performance of the inverter, but also the service life of the system is mainly influenced by it. In the light of the deficiency of the inverter model and control system at the present stage, the structure of a three-phase bridge type of inverter circuit in voltage type is adopted. The control system adopts the double closed loop control of voltage outer loop and current inner loop, and adqaxis decoupling model is deduced. Then, the recursive least square algorithm is adopted to identify the unknown parameters of the model. The actual values of the parameters to be identified are obtained. The identification results show that the identification error is relatively small, and the identification value is very close to the theoretical value. The disturbance experiment is added in the model which further verifies the accuracy and feasibility of the algorithm in the identification of the inverter.

inverter; parameter identification;dqaxis parameter decoupling; recursive least square algorithm

10.3969/j.ISSN.1672-0792.2017.02.004

2016-10-10。

青海省电力公司项目(52280714001D)；青海省光伏发电并网技术重点实验室项目(2014-Z-Y34A)。

TM73

A

1672-0792(2017)02-0021-07

张海宁(1974-)，男，硕士，高级工程师，研究方向为电力系统自动化。