一种配电网节点电压稳定指标分析

王 进，李亚峰，郭绯阳，张 晗

(长沙理工大学 电气与信息工程学院，湖南长沙410114)

一种配电网节点电压稳定指标分析

王 进，李亚峰，郭绯阳，张 晗

(长沙理工大学 电气与信息工程学院，湖南长沙410114)

分析了已有的电压稳定指标使用上的限制以及理论上的缺陷，利用测得的节点电压相量、线路参数等电气量，分析网络潮流计算中电压的二次方程，提出了一种电压稳定指标LV。该指标与已有的指标相比，具有无需判断线路电阻以及受送端功率等优点。最后，通过对IEEE33节点系统仿真，结果表明，LV在系统临近电压崩溃时，该电压稳定指标值更趋近1。由此可得，该方法能够有效地判断系统电压稳定性，适用于电力系统电压稳定性的实时监控。

电压稳定指标；指标比较；系统仿真；电压崩溃；实时监控

0 引言

近年来，世界范围内发生了多起因电压崩溃引起的大面积停电事故。与此同时，我国的电网规模庞大，电压不稳定将对电网的安全稳定运行造成极大的影响[1]。为预防事故，对配电网进行电压稳定分析就成为一项十分必要的工作[2]。

电压稳定从物理意义来讲，就是维持系统的负荷电压运行在某一规定范围内[3]。系统中输送到负荷的功率能否满足其自身需求影响着电压的稳定性。若系统中提供的功率不能满足负荷自身正常运行，那么会导致系统节点电压下降、失稳，严重时电压会发生崩溃现象。近几年，输电线路出现电压不稳定现象，使系统大面积出现停电故障，造成国家财力的巨大损失[4]。为了能够减少配电网络中发生的电压崩溃现象，需要能够实时的对电力系统运行状态进行监控，并且需要对系统可能会出现的电压崩溃现象做出快速、准确地判断[3]88。电压稳定性指标的建立是为工作人员准确判断电压稳定提供依据，它应当能够提供系统母线电压、易出现故障区域等信息，同时能为工作人员解决问题提供参考依据；此外，它还应当具有计算能力强、线性度良好等特点[5];文献[6-7]中需要对不同的负荷进行建模从而得到电压稳定指标，这种方法使得计算过程比较繁琐，并且不同的负荷模型对指标精确度造成不同程度的影响，在复杂的电力系统中该方法不适合推广；文献[8-10]提出了在潮流计算基础上得到电压稳定性指标，并分析它们之间的优缺点；文献[11]提出的基于静态电压失稳概率指标为减小节点电压失稳提供参考依据；文献[12]提出的电压稳定指标时将影响电压稳定的负荷波动等因素考虑在内等。

本文参考文献[13]提出电压稳定指标的方法，根据测得的节点电压的幅值和大小、线路参数等数据，分析潮流计算中电压的二次方程，得到了新的电压稳定指标，最后以 IEEE33节点为例进行仿真，在特定负荷节点上增加负荷功率，来比较新指标与已有指标在系统临近电压崩溃时接近于1的程度。

1 已有电压稳定指标

1.1 静态电压稳定指标

在文献[14]中通过研究系统支路的电压稳定性，依据两节点配电网系统得到电压稳定指标L,其推导过程如下，如图1。

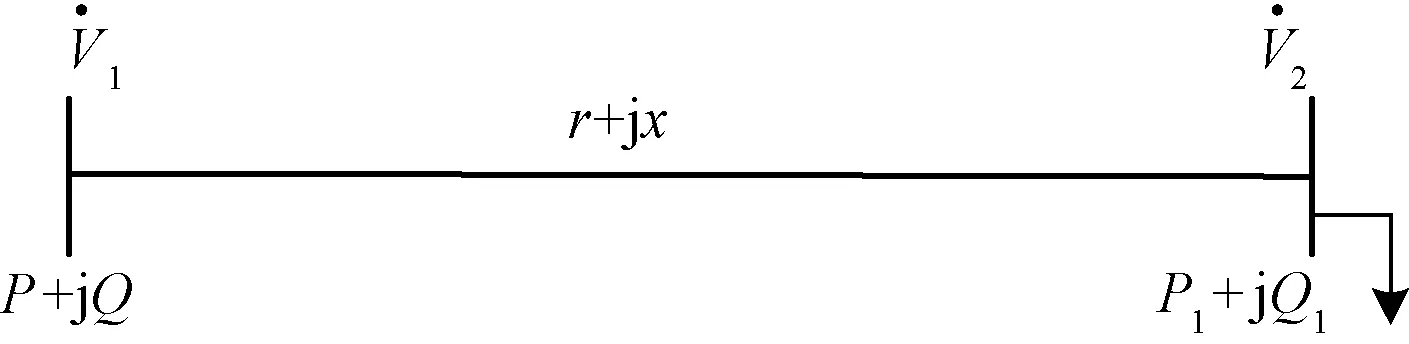
图1 简单两母线系统

其中，r和x分别为线路的电阻和电抗；P、P1分别为送受端的有功功率；Q、Q1分别为送受端的无功功率；V1、V2分别为送受端的电压值。

已知，受端的功率加上网络损耗的功率等于送端发出的功率。即：

(1)

关于P的方程式(1)有实数解的充要条件是方程式的判别式大于等于0，即：

(2)

因此，电压稳定指标为：

(3)

L的大小反映了系统的电压稳定程度，当L越小时，电压越稳定；L越大时，电压越不稳定；当L增大到接近1时，电压临近崩溃。L指标表明系统的总负荷影响电压的稳定性，在推导过程中，将较为复杂的系统等效成简单的两节点系统，这种从网损角度考虑的等效方法得到的指标误差较大，节点电压以及负荷的分布情况等对电压稳定的影响因素在该指标中并未考虑，并且L指标在含分支的配电网中受到局限。

1.2 有功负荷电压稳定指标

文献[15]提出了基于线路有功潮流的电压稳定性指标，该指标推导过程如下，如图2。

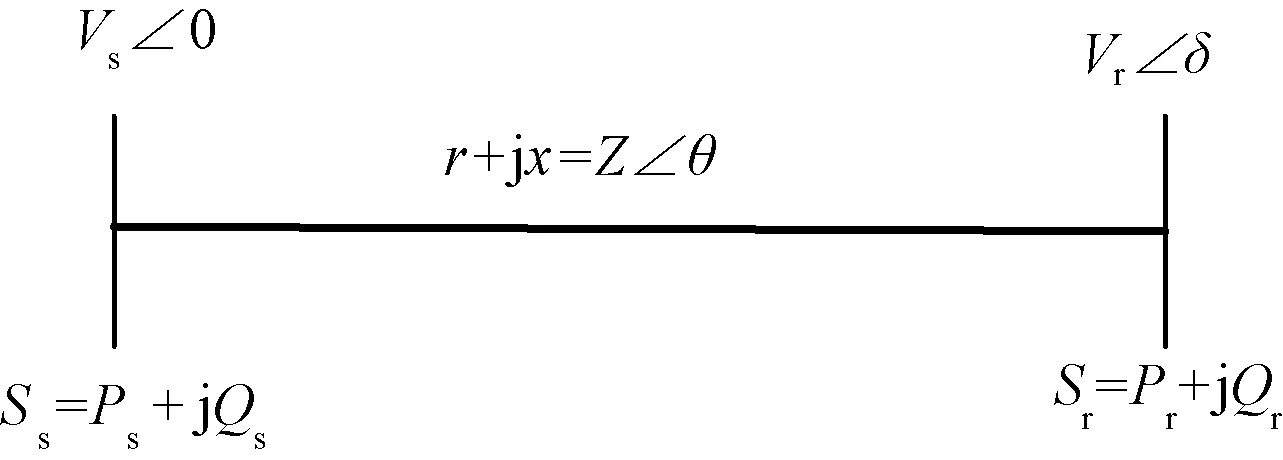
图2 两母线系统

其中，r、x分别为线路的电阻和电抗；δ为线路两端的功角差；θ为线路的阻抗角；Ps、Pr分别为送受端的有功功率；Qs、Qr分别为送受端的无功功率。

(4)

整理得

(5)

公式(5)有实数解的充要条件是判别式大于等于0，即：

(6)

当判别式取等于0时，电压临界点处公式(5)有唯一解。

故得到电压稳定指标为

(7)

Lp的大小反映了系统的电压稳定程度，当Lp越小时，电压越稳定；Lp越大时，电压越不稳定；当Lp增大到接近1时，电压临近崩溃。然而，在使用该指标时，需要考虑线路功率的送受端，并且当线路电阻为0时，Lp不起作用。通过仿真得到，在电压临近崩溃时，Lp并不趋近于1。电压临界点指的是，在某一确定负荷下，电压有唯一解。当方程(5)有唯一解时，Lp在某一确定负荷和功角差下等于1，但是此时功角差不一定是临界点处的值，因此，方程(5)的唯一解不一定是电压临界点。同时，在电压临界点处，方程(5)的判别式不为0，Lp不等于1。

2 新电压稳定指标

负荷的分布情况是电压稳定的重要体现，负荷的母线电压对电压是否稳定具有重要作用。通过对电压稳定指标的分析，已有的指标具有一定的不足，故需要进一步的调整。电压稳定指标应包括影响电压稳定的所有因素，因此，在评估电压稳定的过程中，尤其是系统临近电压崩溃时，应能准确地反映电压稳定情况。文中提出了一种新的电压稳定指标，更好预测电压临近崩溃情况，其推导过程如下，如图3。

图3 新指标下两母线系统

其中，r12、x12分别为线路的电阻和电抗；δ为线路两端的相角差；P2为受端的有功功率；Q2为受端的无功功率；V1、V2分别为送受端电压值。

(8)

经过一系列复杂的计算，整理得：

(9)

公式(9)有实数解的充要条件是判别式大于等于0，即

(10)

由式(9)可得解

(11)

即：

(12)

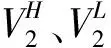
(13)

(14)

对于送端，选取潮流流入为正方向，依据类似的方法可以得到电压稳定指标：

(15)

比较(14)、(15)得，不论线路的送受端，电压稳定指标表达式是类似的，也就是说不需要判别输电线路的受送端功率。本文采用公式(14)作为新指标。

三相辐射状配电网系统可以等效成两母线系统[16]，这种方法可以将新指标Lv推广到N个节点的配电网，将复杂的多节点系统等效为如图3所示的2母线等效系统，等效方法参照文献[17]，连接2个母线线路的等效电阻和电抗分别为：

(16)

(17)

式中：Ploss、Pf分别表示网络中总的有功功率损耗和流经整个网络的有功功率；Qloss、Qf分别表示网络中总的无功功率损耗和流经整个网络的无功功率。

新指标与负荷的视在功率、功率因数有关，同时，它也取决于输电线的导纳以及母线电压和它的向量角。由仿真可得，新指标在系统临近电压崩溃时更接近于1，更好地反映线路电压稳定情况。

3 仿真分析

采用标准IEEE33节点系统(如图4)，进行仿真。该系统有33个节点，总有功功率为3.72 MW，总无功功率为2.29 MVar，该系统网络参数参考文献[18]。仿真中，向特定节点增加负荷功率，从100 kW开始每次增加100 kW，直至电压发生崩溃。选取节点32、17进行仿真分析，研究不同功率因数下，3个电压稳定指标的变化趋势。横坐标代表系统负荷总有功功率(标幺值)，即系统负荷总有功功率与基准有功功率(3.72 MW)比值，纵坐标代表不同电压稳定指标值。

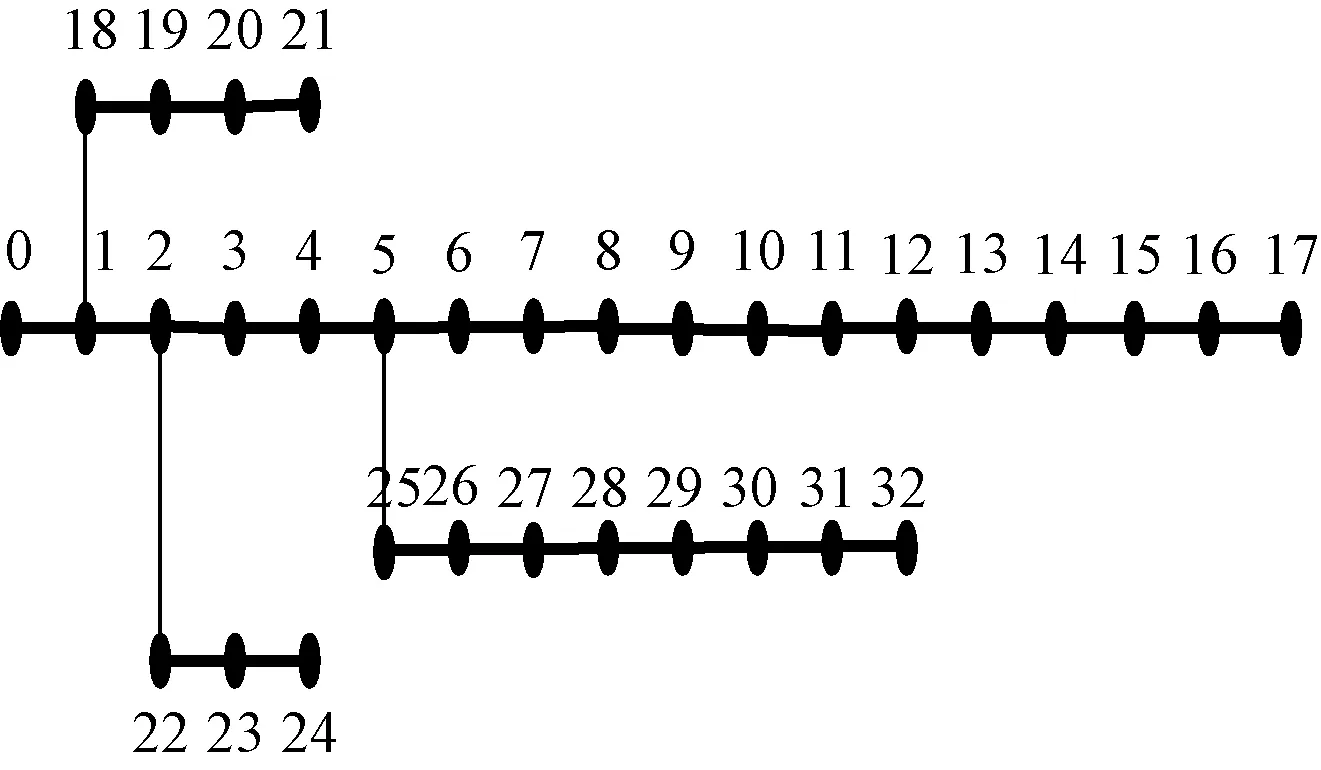
图4 IEEE33节点配电系统图

不同功率因数下，节点32、节点17临近电压崩溃时负荷功率值如表1。

表1 33节点系统中临界电压崩溃时负荷功率值

(1)在节点32上增加负载功率，进行仿真并分析3个电压稳定指标值变化情况。在功率因数分别为0.5、0.8时，向节点32逐渐增加负荷功率，直至电压临近崩溃，其他节点保持不变。仿真结果如图5、6。

图5 功率因数为0.5时，节点32随着总有功功率增加电压稳定指标值

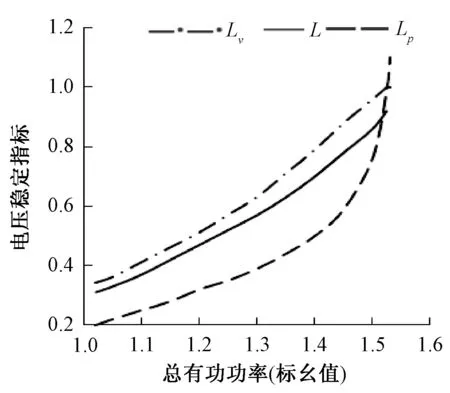
图6 功率因数为0.8时，节点32随着总有功功率增加电压稳定指标值

由仿真图5、6可得，随着节点32负荷功率的不断增加，3个电压稳定指标值都随之上升。在电压临进崩溃时，新指标Lv在不同的功率因数下均趋近于1；Lp即有功负荷电压稳定指标在功率因数为0.5时，其值小于1，在功率因数为0.8时，其值大于1；在不同的功率因数中，L即静态电压稳定指标的值均远小于1。因此，新指标较已有指标更能准确地反映电压稳定情况，预测整个系统是否发生电压崩溃。

(2)在节点17上增加负载功率，进行仿真并分析3个电压稳定指标值变化情况。在功率因数分别为0.7、0.9时，向节点17逐渐增加负荷功率，直至电压临近崩溃，其他节点保持不变。仿真结果如图7、8。

图7 功率因数为0.7时，节点17随着总有功功率增加电压稳定指标值

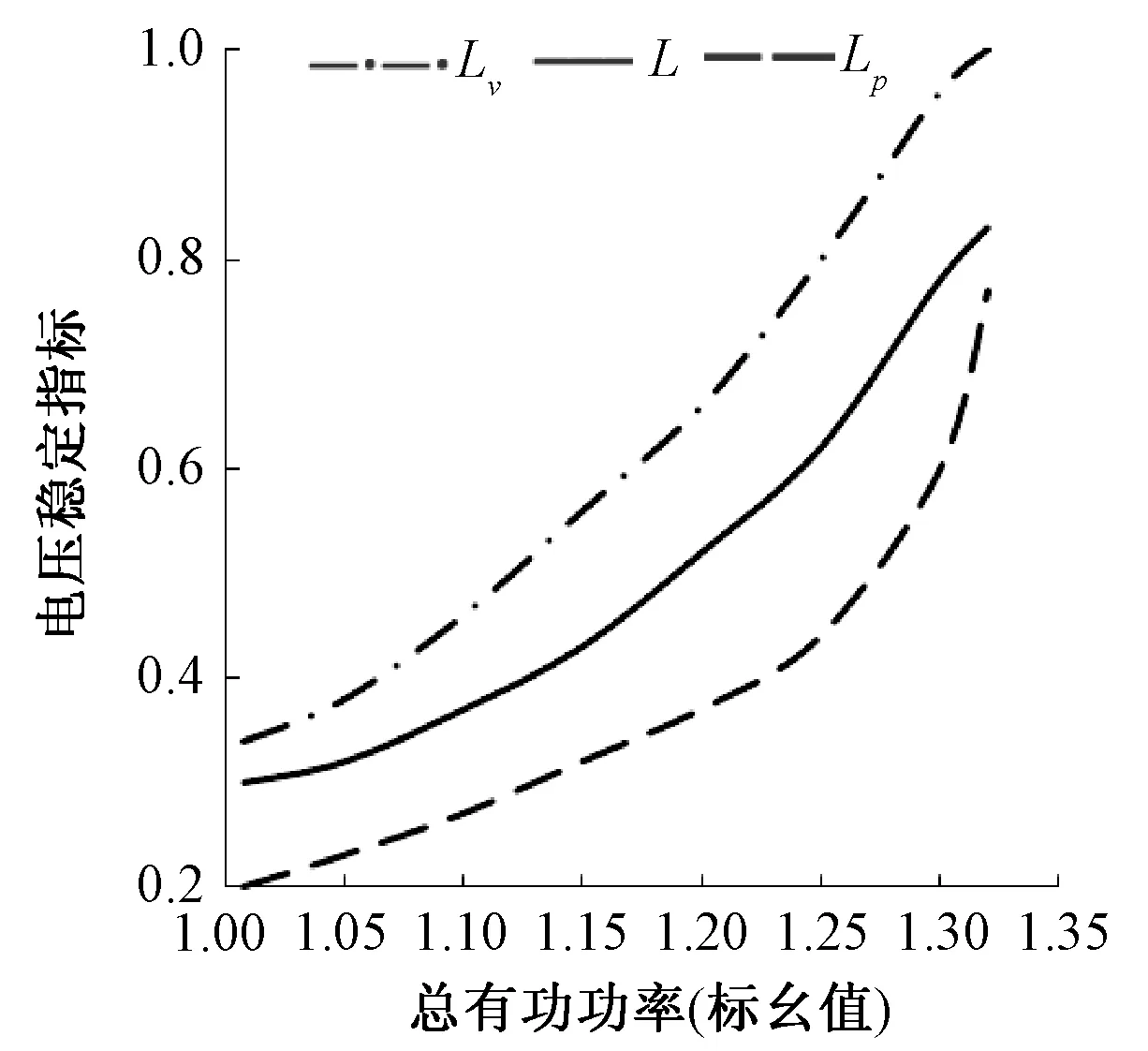
图8 功率因数为0.9时，节点17随着总有功功率增加电压稳定指标值

由仿真图7、8可得，随着节点17负荷功率的不断增加，3个电压稳定指标值都随之上升。在电压临进崩溃时，新指标Lv在不同的功率因数下均更趋近于1；不同的功率因数中，Lp、L的值都远小于1。因此，新指标较已有指标更能准确地反映电压稳定情况，预测整个系统是否发生电压崩溃。

4 结论

文中提出的新电压稳定指标与已有的指标相比，具有不用判断线路电阻的阻值以及受送端功率、线性度好等优点。最后由仿真结果可得，在系统电压临近崩溃时，新指标更趋近于1，可以更好地说明线路电压是否稳定。本文所提出的方法有利于提高系统电压稳定精度并且为调度人员评估电压稳定提供更好的依据。

[1]王云鹏,韩学山,孙东磊,等. 考虑直流输电控制方式的受端电网电压稳定性机理分析[J]. 电力系统自动化,2016，40(6)：35-41.

[2]吴昊,董文辉. 基于改进人工鱼群算法的连续潮流电压稳定性研究[J]. 电气自动化,2014,36(2):69-71，77.

[3]朱星阳，张建华，刘文霞，等.风电并网引起电网电压波动的评价方法及应用[J].电工技术学报，2013，28(5):88-98.

[4]秦文丽,林伟芳. 在线电压分析方法及无功优化配置综述[J]. 电气传动自动化,2013,35(1):1-6.

[5]周念成，钟岷秀，徐国禹，等.基于电压相量的电力系统电压稳定指标[J].中国电机工程学报，1997，17(6):425-428.

[6]邓卫, 唐西胜, 裴玮, 等. 含风电微型电网电压稳定性分析及控制技术[J]. 电工技术学报, 2012,27(1): 56-62.

[7]李大虎, 曹一家. 基于同步相量测量的实时电压稳定分析方法[J]. 电力系统自动化, 2006, 30(12): 17-22.

[8]MOGHAVVEMI M, OMAR F M. Technique for contingency monitoring and voltage collapse prediction[J]. IEE Proceedings-generation Transmission and Distribution, 1998, 145(6):634-640.

[9]傅旭,付翀丽,黄明良. 一种提高电力系统静态电压稳定裕度的切负荷算法[J]. 电力建设,2014,35(9):71-75.

[10]胡金理,刘曼,成涛,等. 含分布式电源的配电网无功优化[J]. 电力学报,2015,30(2):117-122.

[11]马平, 蔡兴国. 估计支路型事故后系统电压稳定边界的灵敏度算法[J]. 中国电机工程学报, 2008, 28(1): 18-22.

[12]巩伟峥,房鑫炎.基于广域测量系统的电压稳定指标[J].电网技术, 2011,35(4):71-75.

[13]JASMON G B, LEE L.Stability of load flow techniques for distribution system voltage stability analysis[J].Generation Transmission and Distribution[see also IEE Proceedings-Generation,Transmission and Distribution],IEE Proceedings C,1991,138(6):479-484.

[14]JAMSON G B, LEE L. New contingency ranking technique in corporating voltage stability criterion[J].IEE Proceedings-Generation Transmission and Distribution,1993,140(2):87-90.

[15]卢锦玲，石少通，卢洋.含大规模风电场的电网静态电压稳定性评估[J].电力系统及其自动化学报，2015，27(6):73-80.

[16]DAS D, KOTHARI D P,KALAM A.Simple and efficient method for load flow solution of radial distribution networks[J].International Journal of Electrical Power & Energy Systems, 1995,17(5):335-346.

[17]BARAN M E,WU F F.Network reconfiguration in distribution systems for loss reduction and load balancing[J].IEEE Transactions on Power Delivery, 1989,4(2):1401-1407.

[18]黄红程,顾洁,方陈. 基于无向生成树的并行遗传算法在配电网重构中的应用[J]. 电力系统自动化,2015,39(14):89-96.

A New Analysis on Nodal Voltage Stability Index of Power Distribution Network

WANG Jin, LI Yafeng, GUO Feiyang, ZHANG Han

(College of Electrical and Information Engineering, Changsha University of Science and Technology, Changsha 410114, China)

The restrictions on the usage and theoretical defects of the existing indices for the voltage stability have been pointed out in the paper．By utilizing the measured electric data such as bus voltage phasors, line parameters, and according to the voltage quadratic equations of power flow，a new voltage stability indexLvis proposed．Comparison between the proposed voltage stability index and previous stability ones has been conducted and the results show that the newly proposed index possesses the following advantages: no need for judging the line resistance and sending end power and so on. The performance of the new index is tested based on IEEE33．The result of simulation shows that when the load approaches the critical point, the value ofLvapproaches 1 more than previous indices．Therefore, the proposed index is favorable to determine voltage stability and implements real-time monitoring of the power system．

voltage stability index; index comparison; system simulation; voltage collapse; real-time monitoring

10.3969/j.ISSN.1672-0792.2017.02.002

2016-09-04。

TM712

A

1672-0792(2017)02-0009-05

王进(1972-)，女，副教授，研究方向为电力系统运行与控制,分布式电源规划。