单电压闭环逆变器数字控制器设计

王卉隽，胡 锴

（1. 中国船舶工业综合技术经济研究院，北京100081；2. 中国舰船研究设计中心，武汉 430064）

单电压闭环逆变器数字控制器设计

王卉隽1，胡 锴2

（1. 中国船舶工业综合技术经济研究院，北京100081；2. 中国舰船研究设计中心，武汉 430064）

分析了单相逆变器数字控制实现时零阶保持器对系统的影响。利用朱利判据求取了单电压环控制下使系统稳定的控制参数，并从求取的区域中选择几组控制参数进行仿真。仿真结果表明所求取稳定区域的正确性，利用朱利判据求得的稳定区域在实际设计控制器时具有很好的指导意义。

单电压闭环 数字控制器 朱利判据

0 引言

逆变器是将直流电变换为交流电的装置。传统的逆变器多采用模拟控制，随着大规模集成电路技术的发展，逆变器全数字化控制的应用日益增多。数字控制相比模拟控制有很多优势，但受器件发展的限制，数字控制方式存在着特定的问题，如采样和量化过程产生的误差，数字处理器采样、计算延时带来最大占空比受限等。这些问题使得系统的性能有所下降，从而影响了数字控制技术优点的充分发挥[1]。

本文将以单相逆变器为研究对象，对数字控制的单电压闭环逆变器进行PI控制器分析设计。首先分析了零阶保持器的引入对系统的影响，再在Z域下对控制系统进行分析设计，利用朱利判据求取控制参数的稳定区域，再利用伯德图对区域中参数进行深入分析，以选取合适参数，最后从求取的区域内选择几组控制参数进行时域仿真和器件级仿真，验证了控制器参数设计的准确性。

1 离散域数学模型

本文以一台3 kW工频逆变器为研究对象，主电路图如图 1所示。电路具体参数如下：Vdc=360 V，uo=220 V，Po=3 kW，Hv=0.02，Lf=0.8 mH，Cf=10 uF，R=16 Ω，fc=10 kHz，fk=20 kHz，Vtri=1。

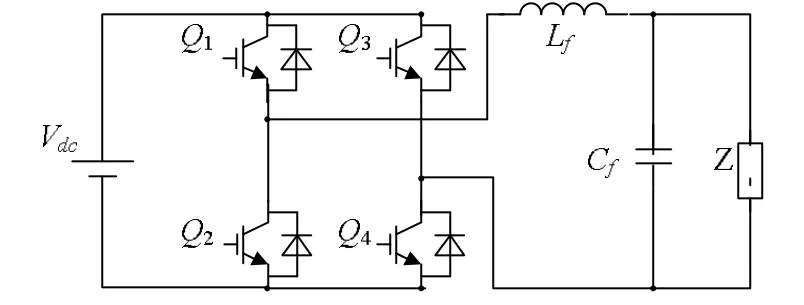
图1 单相全桥逆变器主电路图

调制方式采用单极倍频调制，其中 Vtri为三角载波幅值，则有：

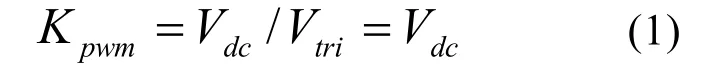
逆变器的主电路等效框图如图2所示。

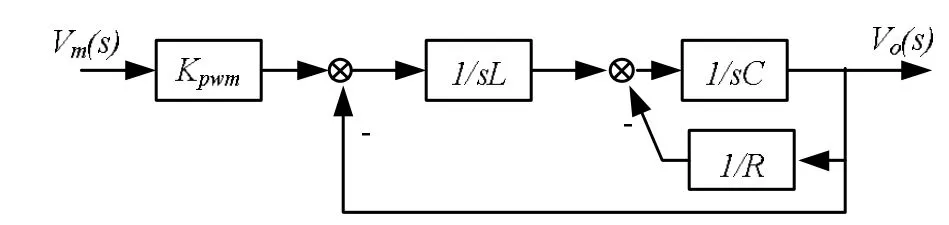
图2 逆变器主电路等效框图

由此可得逆变器调制器输入到输出的S域传递函数为：

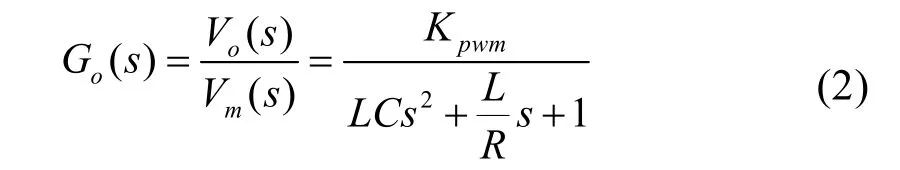
单电压闭环控制框图如图3所示。

图3 单电压闭环控制框图

图中，零阶保持器S域传递函数为：

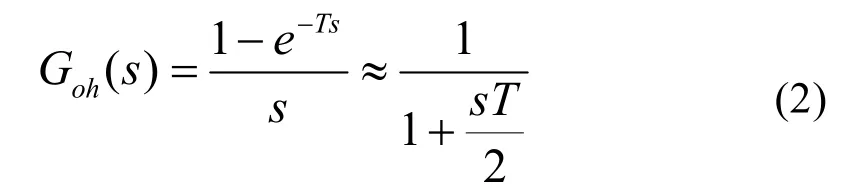
下面推导包含零阶保持器的广义被控对象的离散模型：

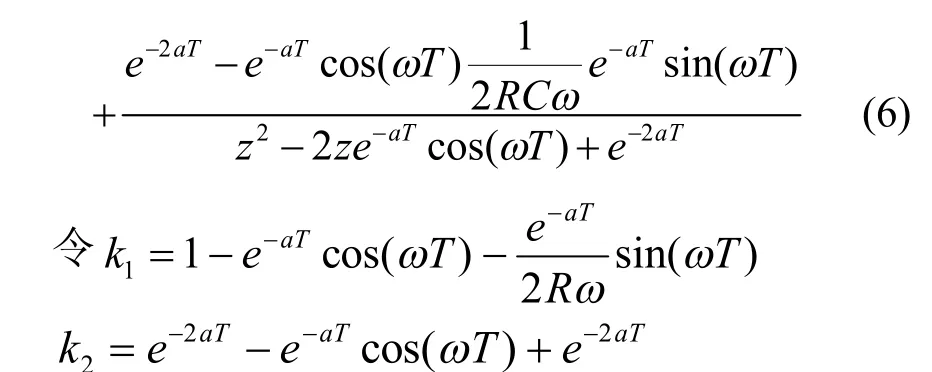
则广义被控对象的离散数学模型为：

2 零阶保持器对逆变器的影响

逆变器利用数字控制方式实现时，由于零阶保持器的引入，包含零阶保持器的系统传递函数不仅与逆变电源的控制参数有关，还跟采样周期有关，系统的一系列特性也将发生变化。

由公式(2)可知，零阶保持器可以等效为一阶惯性环节，会对原系统带来相位滞后和加速系统高频段的衰减。连续系统和加入零阶保持器后系统伯德图如图4所示。

图4 连续系统和离散系统伯德图

从图中可知，原连续系统为稳定系统，但由于零阶保持器的引入，造成系统相角滞后，离散后的系统不再稳定。如果不考虑零阶保持器的影响直接对系统进行分析设计，可能会出现连续系统稳定，而离散后系统不稳定，从而控制参数无法使用。

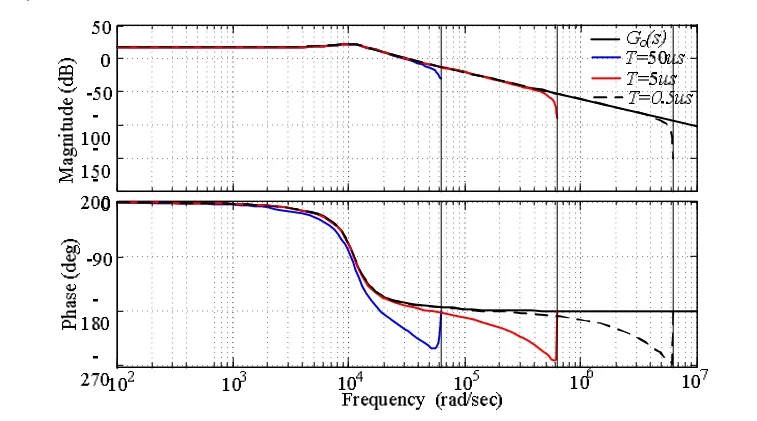
图5 不同采样周期离散系统伯德图

离散系统伯德图与采样周期的关系如图5所示。随着采样周期的增大，零阶保持器造成的相角滞后越大，采样周期越小，离散系统频率特性越接近连续系统，当采样周期足够小时，零阶保持器对系统的影响就可以忽略。由于实际应用中，逆变器采样频率一般选为开关频率，因此零阶保持器对系统的影响不能忽略，在对系统进行设计分析时必需考虑。

3 离散控制系统稳定性分析

稳定性是控制系统最关键的因素。判断闭环系统稳定的方法很多，如判断闭环极点的位置，朱利稳定判据[2]，劳思-赫尔维持稳定判据。本文利用朱利稳定判据求取系统稳定条件，根据稳定条件确定控制参数合理区域，以作为控制器设计时的参考。

朱利判据是直接在Z域内应用的稳定判据。朱利判据直接根据离散系统闭环特征方程D(z)=0的系数，判断闭环极点是否全部位于z平面上的单位圆内，从而判断系统的稳定性。

从前面分析可知，零阶保持器的引入使系统性能差，本文利用PI控制器，即一阶滞后控制，对包含零阶保持器的逆变器进行补偿。PI控制器S域传递函数为：

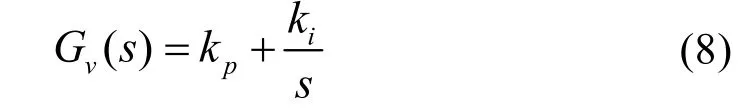
离散化后Z域表达式：

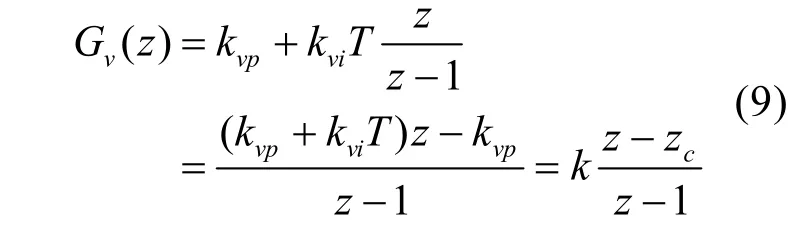
则由控制框图可得，离散系统的特征方程为：

将公式(7)、(8)带入式(10)可得：

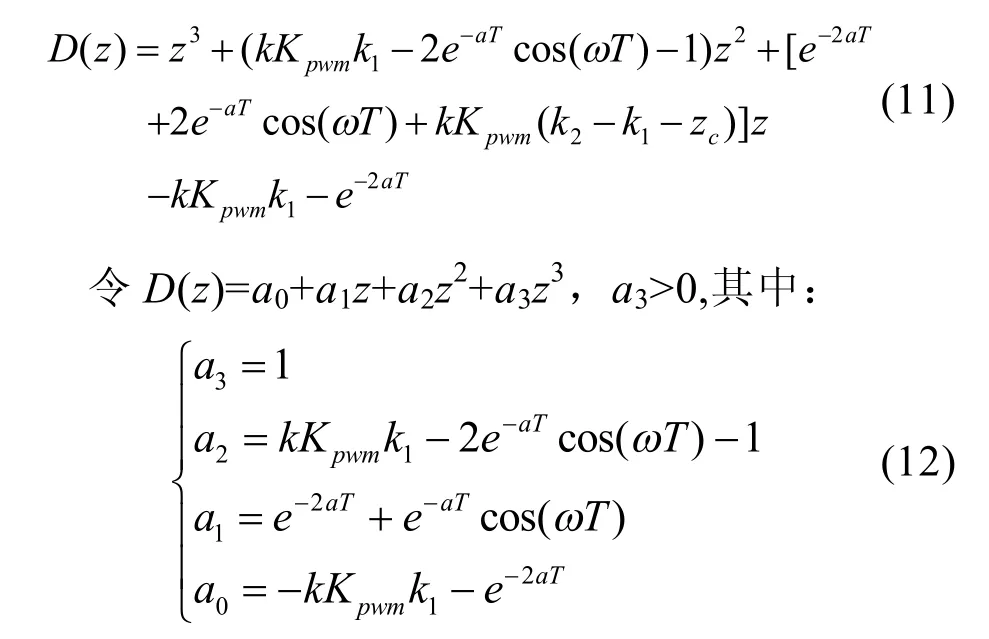
列朱利表：

行数 z 0 z 1 z 2 z 3 1 a0a1a2a32 a3a2a1a0

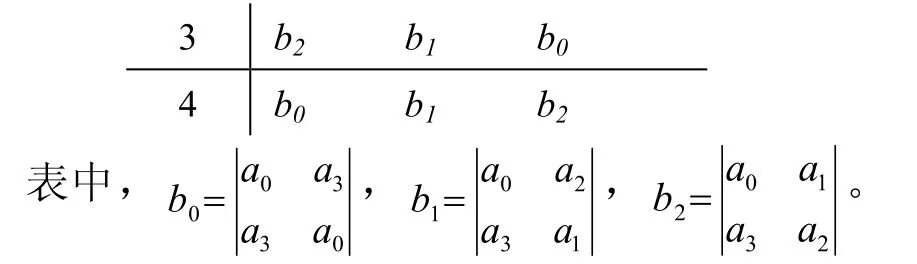
根据朱利判据有：

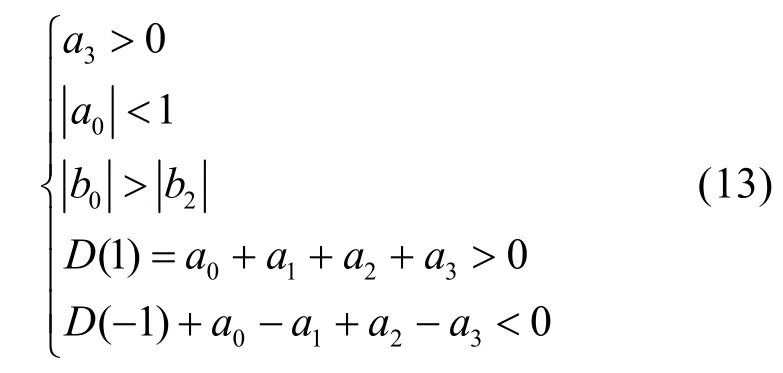
根据(13)中式子可以确定控制参数k，zc的范围，实际应用中可在所求范围中选取，再结合校正后系统开环伯德图判断系统的性能。

4 仿真分析

根据前文分析，选择几组控制参数，利用matlab/simulink和saber进行仿真分析。

由公式(7)、(8)可得校正后离散系统开环传递函数为：

在稳定区域内选如下参数进行分析：

k=0.005、zc=0.4，k=0.05、k=0.05、zc=0.8

在稳定区域外选择如下控制参数分析：

k=0.4、zc=0.4，k=0.05、zc=1.1

下面分别绘制在各控制参数下，校正后系统伯德图。

图6三条曲线分别为连续系统、离散后以及校正后伯德图。从图中可知，连续系统本身是一个稳定系统(稳定余度很小)，离散后，由于零阶保持器的引入，使系统相交滞后，高频段衰减变快，不再为稳定系统。随着滞后校正装置的串入，校正后系统稳定。

图7为校正装置零点不变，增益逐渐增大，由稳定变为不稳定。从伯德图中，可知，k=0.005时，系统相角裕度89.6°，幅值裕度24 dB，为稳定系统，但穿越频率只有433 rad/s，低频增益也小，这在实际系统体现为动态响应慢，稳态精度差。随着 k增大，k=0.05，系统相交裕度降低，幅值裕度也降低，但截止频率增大，低频增益变大，系统的动态性能得到改善，稳定性得以加强，即牺牲了系统的稳定性，提高了系统的动态和稳态系能。如果k增加超过某个值，约为0.09，系统将变为不稳定系统，如图 7所示，k=0.4时，系统不再稳定。

图8为校正装置的系数k不变，改变零点zc值时校正系统伯德图。从图中可知，随着zc增大，会增大系统的相角裕度和幅值裕度，但会降低系统的稳定性，而且稳定时会增加系统的稳态误差。当zc＞1时，系统不再稳定，系统存在单位圆外的闭环极点。

从上面分析可知，在稳定判据求取的控制参数限制区域内的参数k，zc，系统频域内也是稳定的。下面对所选择的几组控制参数进行系统级仿真和器件级仿真。

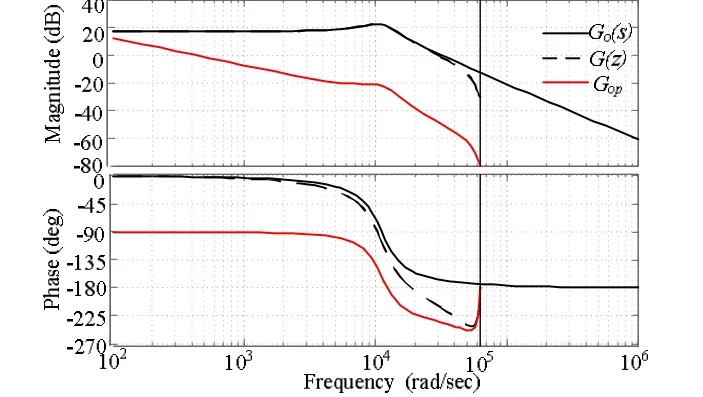
图6 k=0.005, zc=0.4

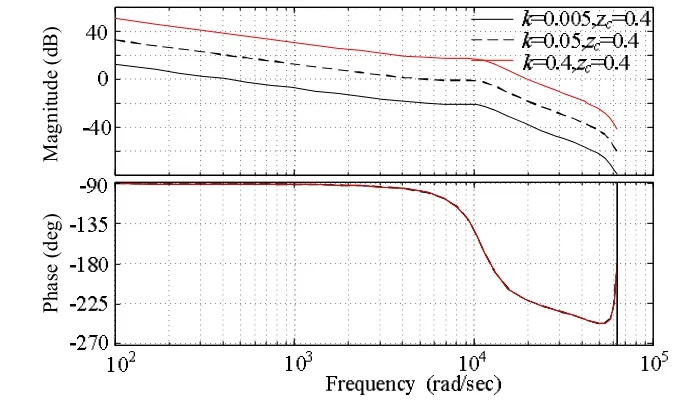
图7 k=0.005、k=0.05、k=0.4,zc=0.4

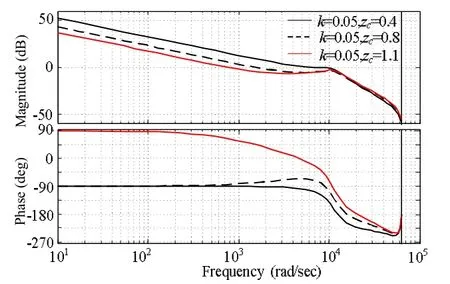
图8 k=0.05, zc=0.4、zc=0.8、zc=1.1

图9为不同控制器参数时系统仿真波形，图(a)、(b)、(c)中，调节时间分别为6.875 ms，2 ms，2.32 ms。这与前面从伯德图中分析结果相吻合。图(d)为控制参数在不稳定区域时仿真波形，验证了前面不稳定分析的正确性。

下面选两组控制参数进行器件级仿真：从上面分析，选取稳定性能相对较好的一组控制参数，k=0.05，zc=0.4(但超调较大)；选择一组系统不稳定的控制参数，k=0.4，zc=0.4。仿真结果分别如图10(a)、(b)所示。

图9 不同控制参数时系统级仿真波形

图10验证了前面理论的分析正确性，证明了基于稳定性求取控制参数的可行性，也证明了系统频域特性和时域特性分析对设计实际控制系统的价值。

5 总结

本文以单相逆变器为研究对象，对数字控制的单电压闭环逆变器进行PI控制器分析设计。连续系统离散化时，由于零阶保持器的引入，系统会受采样周期的影响，采样周期越短，影响越小。利用朱利稳定判据能确定使系统稳定的控制参数，结合系统的伯德图能选择最优的控制参数。系统的时域特性和频率特性能很好的反映实际系统，对系统的分析设计具有很好的指导作用。

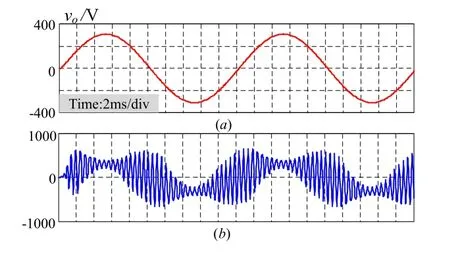
图10 器件级仿真结果

[1] 孔雪娟. 数字控制PWM逆变电源关技术研究[博士学位论文]. 武汉: 华中科技大学, 2005.

[2] 卢京潮. 自动控制原理. 西安: 西北工业大学出版社, 2009.

[3] 赵广元. MATLAB与控制系统仿真实践. 北京: 北京航空航天出版社, 2009年.

[4] M. P. Kazmiekowski and L. Malesani, Current control techniques for three-phase voltage-source PWM converters: A survey. IEEETrans. Ind. Electron., 1998, 45(5): 691-703.

Design of the Single Voltage Closed-loop Inverter Digital Controller

Wang Huijun1, Hu Kai2

(1. China Institute of Marine Technology＆Economy, Beijing 100081, China; 2. China Ship Development and Design Center, Wuhan 430064, China)

The effect of the zero order holder used digital control method on the single-phase inverter is mainly investigated in this paper. The control parameter under single voltage control is obtained by the method-the Jury test which can make system stability. The results of the simulation verify the correctness of stable regions, which can fulfill the controller design requirements of stable regions used Jury test．

Single voltage Closed-loop, Digital controller, Jury test

TM464

A

1003-4862（2017）02-0067-04

2016-09-29

王卉隽（1983-），女，工程师。研究方向：舰船自动化技术标准研究。E-mail: whsm3999@163.com