不可逆热声制冷机的Ω函数优化
2017-03-14蒋智杰吴锋田一泽
蒋智杰,吴锋,田一泽
(武汉工程大学机电工程学院,湖北 武汉 430073)
不可逆热声制冷机的Ω函数优化
蒋智杰,吴锋,田一泽
(武汉工程大学机电工程学院,湖北 武汉 430073)
根据热声制冷机参数振荡的特点,建立复指数传热规律不可逆热声制冷机循环模型.提出Ω=(2ε-1)R/ε的优化目标函数.在考虑热阻、热漏、内不可逆性等不可逆因素的情况下,利用有限时间热力学,分析不可逆热声制冷机各性能参数的优化关系.
热声制冷机;复指数传热;有限时间热力学;优化
0 引言
不同于传统的蒸汽压缩式制冷机,热声制冷技术[1-3]是21世纪全新的技术.它的工作原理是声致热效应[4],在特定的气体工质在声振荡的作用下与回热器固体壁面附近产生反声传播方向的时均热流,从而降低或保持低温端温度,达到制冷的目的.热声制冷机有低污染、无运动部件,克服了传统制冷的寿命短、工作效率低的缺点,成为下一代制冷机的发展方向.最早研究卡诺制冷机的最优性能时,将实数作为传热指数分析.但在实际传热中,由于声管道中纵向压力的振荡,工质流体的温度也会以同样的频率振荡,因此,考虑声弛豫现象,工质的温度用复数[5-7]表示更为准确.本文中建立复指数传热规律下的广义不可逆热声制冷机循环模型,运用有限时间热力学[8]求出复指数规律下的制冷率和制冷系数,通过数值计算分析在不同传热指数、不同热阻的条件下目标函数的最优值[9-10],通过比较分析为以后的设计实验提供帮助.
1 热声制冷机热力学循环分析

图1 热声制冷机模型
热声制冷机主要由冷热端换热器、回热器、热声器件、谐振管组成,在不可逆热声热机模型中工质与热源之间有热阻,传热在有限的温差下进行.工质在传热过程中与高温端换热时平均温度THO、与低温端换热时平均温度TLO,换热器两端温度有THO>TH>TL>TLO的关系.工质温度可表示为THC=THO+T1eiω,TLC=TLO+T2eiω,式中T1,T2为第一级声量,ω为振荡频率,高温热源TH、低温热源TL为常值,如图1所示.
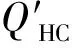
式中K1、K2分别为工质与高温端、低温端的传热系数,F1、F2分别为高温端换热器、低温端换热器的传热面积.n=n1+in2为复数,且虚部n2反应了热传播过程的热弛豫现象.sgn(n1)是关于n1的函数.

(1)
(2)
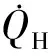
(3)
引入不可逆因子φ:
(4)
以上的公式中,若φ=1且q=0,则系统为内可逆模型;若φ>1且q>0,则系统为有热阻、热漏的不可逆模型;若φ=1且q>0,则系统为有热阻和热漏的模型;若φ>1且q=0,则系统为热阻不可逆模型.
2 目标函数Ω的建立
在仅有热漏q、热阻Rth的制冷机循环模型中,由热力学第二定理得:
QHC/THO=QLC/TLO
(5)
设x=TLO/THO并联立(1)、(2)、(5)式,可得到工质的平均温度TLO、THO与高低温热源TL、TH的关系:
(6)
(7)
“你们不能这样。我在老家就知道《小二黑结婚》《王贵与李香香》,我们现在是新中国的新女性,更要反对包办婚姻。我不能嫁给杨连长,我坚决不同意。这个小伙子不行,就另找别人,反正我不嫁给又老又丑的杨连长。谁说也不行!”田志芳几乎是疯了一样地喊叫着。
(8)
(9)
由热力学第一定律求出热声制冷机制冷率R′和制冷系数ε′的表达式:
(10)
(11)
联立(9)、(10)式,求出复指数传热规律下不可逆热声制冷机制冷率的实部R:
其中A、B分别为TL-(TH/x)n的实部和虚部,经过转换可得:

联立(8)、(9)、(11)式,得出热声制冷机的制冷系数ε′:
(12)
联立(8)、(9)、(10)、(11)、(12)式,得出目标函数Ω:
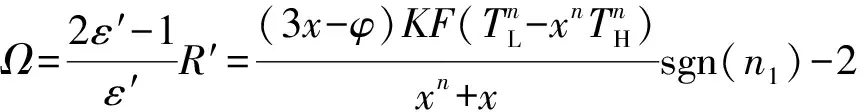
考虑目标函数Ω的实部Re(Ω):

3 数值计算
采用复指数传热规律下的不可逆模型计算,取值如下:TH=310 K,TL=280 K,k=1 200 W/K,F=0.01 m2,取n=1+in2,n2=0.05、0.10、0.15,φ=1.00、1.05、1.10,q=20、40、60 w,x=[0,1].代入以上各式取得数据,作图分析.

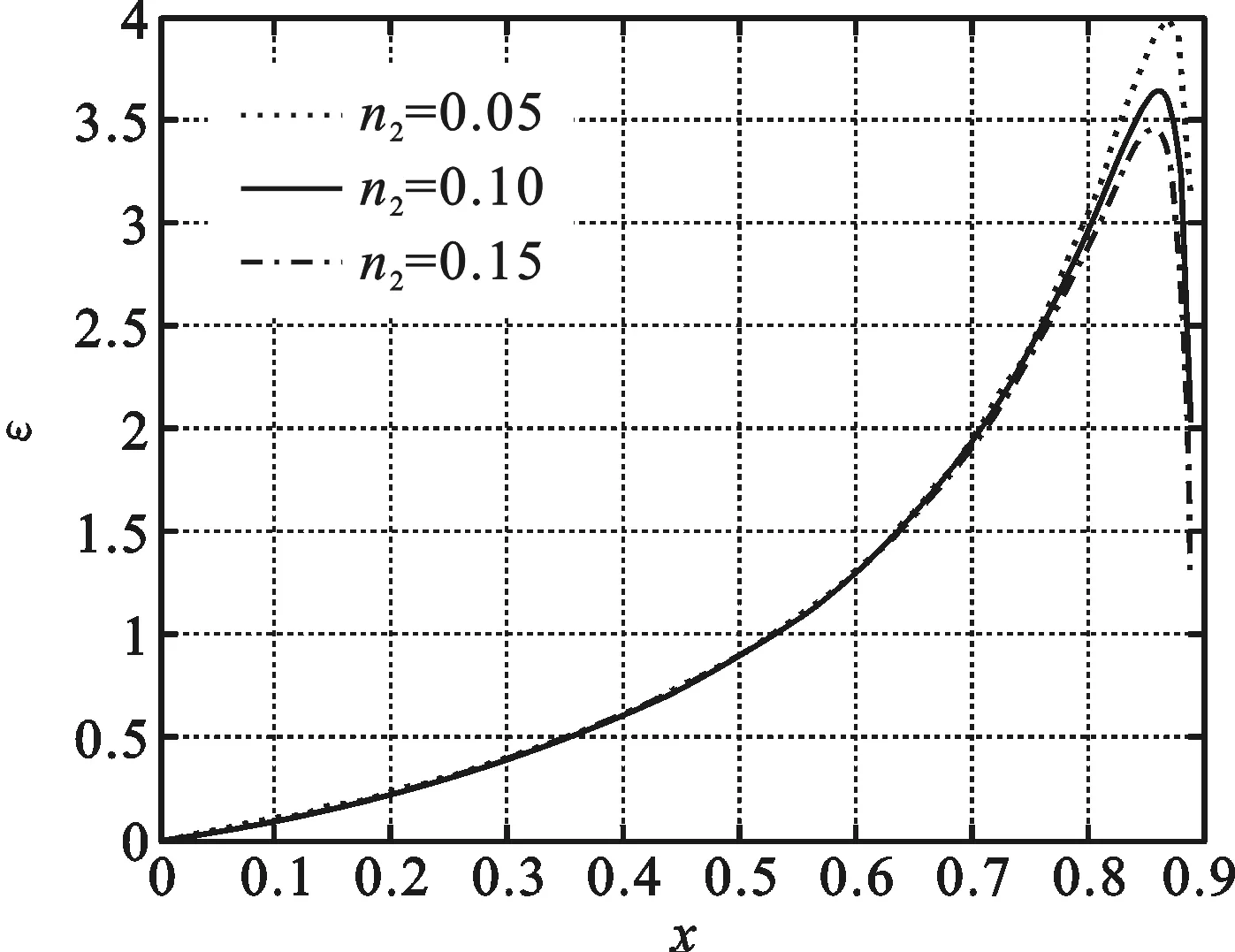
图2 不同虚部数值n2时制冷系数ε和工质低高温度比x的关系曲线

图3 不同不可逆因子φ时制冷系数ε和工质低高温度比x的关系曲线



图4 虚部数值n2=0.05、不同热漏q时目标函数Ω和工质低高温度比x的关系曲线

图5 虚部数值n2=0.10、不同热漏q时目标函数Ω和工质低高温度比x的关系曲线

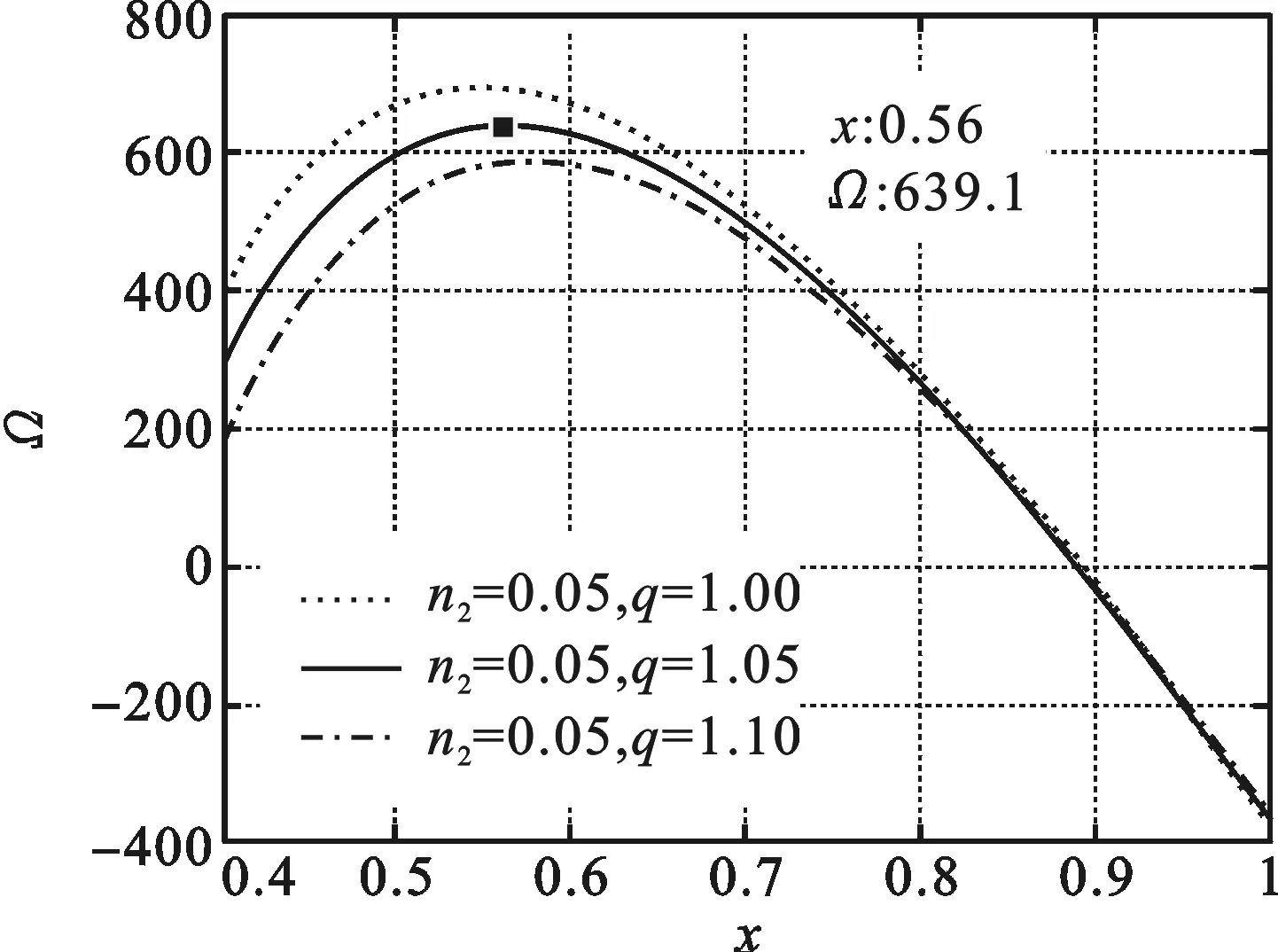
图6 虚部数值n2=0.05、不同不可逆因子时函数Ω和工质低高温度比x的关系曲线
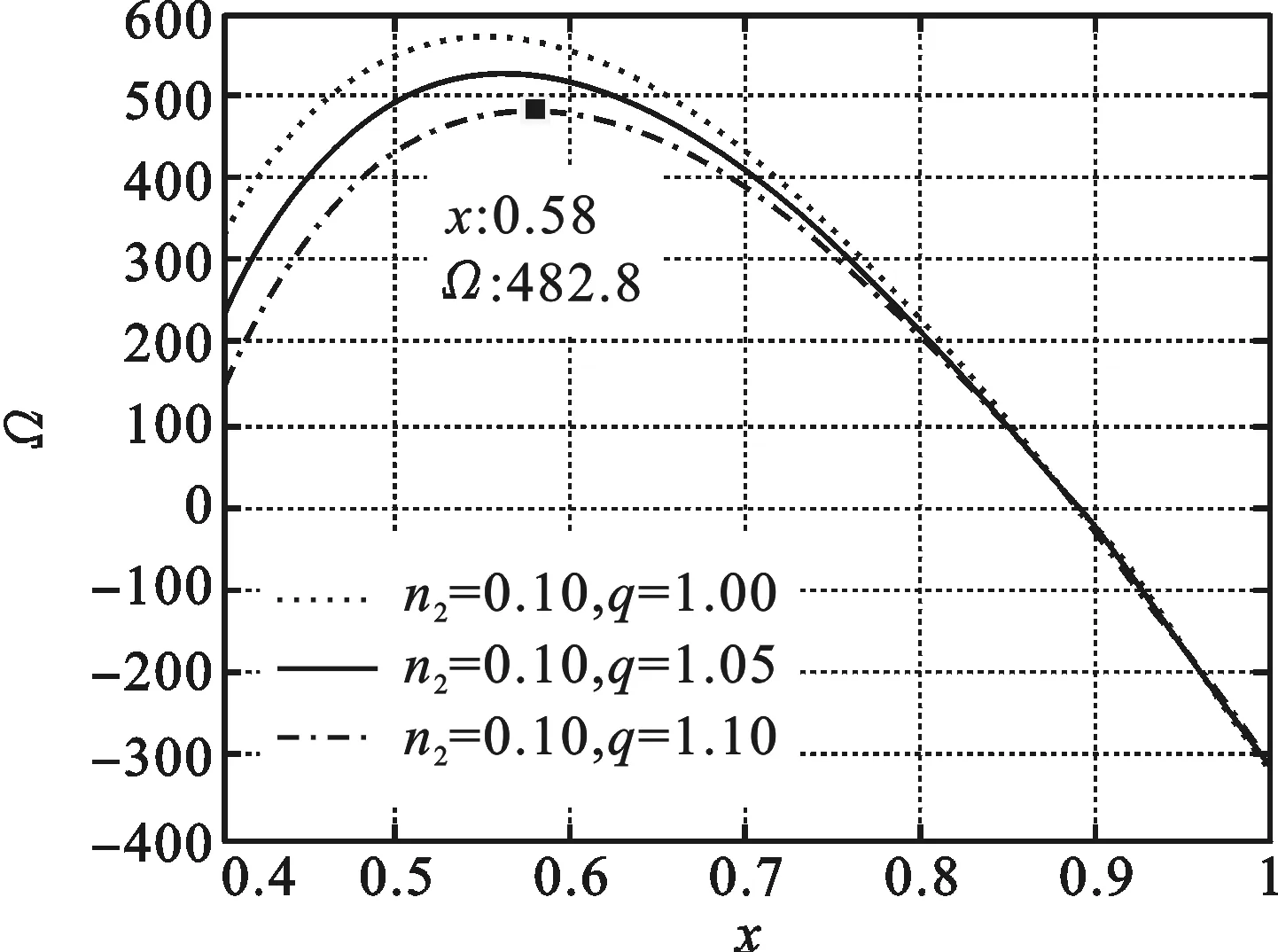
图7 虚部数值n2=0.10、不同不可逆因子时函数Ω和工质低高温度比x关系曲线
图8是制冷率R与制冷系数ε的Ω-ε关系曲线,图9是目标函数Ω与制冷系数ε的R-ε关系曲线,曲线均呈回环趋势.结合图8与图9,随着工质高低温比x的变化,当ε取最大值时制冷率R往往很小,从而导致目标函数Ω值并不理想.当制冷率R最大时,由所对应的ε值知,此时函数Ω值并不是最优.比如虚部n2为0.15时,当制冷率R达到最大值Rmax时,ε=0.06,此时函数Ω值并不是最优;当ε=1.20时,目标函数Ω达到最大值Ωmax,此时设备综合性能最优,这是系统的最佳协调平衡点.
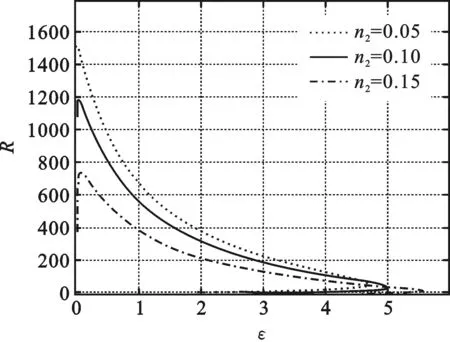
图8 制冷率R与制冷系数ε的关系曲线
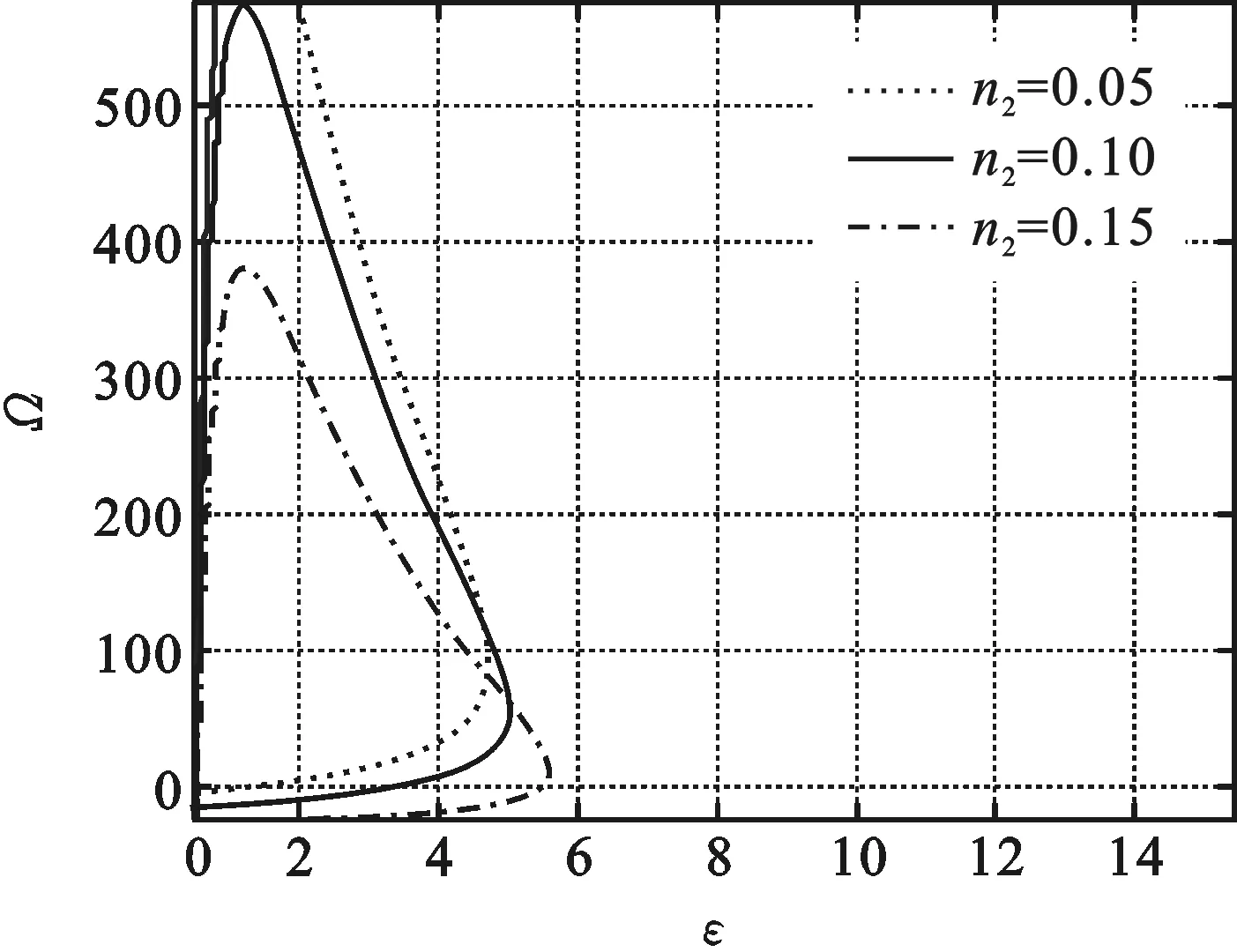
图9 目标函数Ω与制冷系数ε的关系曲线
4 总结
不可逆热声制冷机各个参数错综复杂,目标函数Ω的特殊性意义是为系统提供一个综合性的优化标准.其优点是,目标函数Ω并不像火用或者生态作为目标函数时那样,式中并没有明确的熵表达式被应用或者任何的环境参数被应用,而是用简洁的函数结构反映热机综合性能.要使目标函数Ω达到最优值,需调整多个参数,适当降低传热指数虚部数值n2、热漏q、不可逆因子φ,均使目标函数Ω增大.结果表明,不可逆因子φ一定时,该模型下工质低高温比值x=0.55时,目标函数Ω取得最大值Ωmax,达到设备最优化的效果.
[1] 鄂青,沈秋婉,陈秋霞. 热声制冷机[J].真空与低温,2009, 15 (2):117-120.
[2] 吴锋,李青,郭方中,等. 热声理论的研究进展[J].武汉工程大学学报,2012,34(1):1- 6+73.
[3] 鄂青,刘益才,郭方中. 微型热声制冷机设计方案研究[J].真空与低温,2004, 10 (2):43- 47.
[4] 沈国清,于岩,杨永钊. 热声热机的热力学分析[J].节能,2006(1):21- 24+2.
[5] 林杰. 热声热机系统的性能优化研究[D].武汉:武汉工程大学,2014.
[6] Wu F,Wu C,Guo F,et al. Optimization of a thermoacoustic engine with a complex heat transfer exponent[J].Entropy, 2003,5(5):444 - 451.
[7] 阚绪献,吴锋,张晓青, 等. 热声热机微热力学循环的最优性能[J].武汉理工大学学报,2009, 31 (14):130-133.
[8] 阚绪献,吴锋,张晓青, 等. 复杂传热规律下热声制冷机最优性能[J].华中科技大学学报(自然科学版),2008, 36 (12):91- 93.
[9] 何秋石,吴锋,陈浩, 等. 包含直线过程的热声微循环有限时间热力学优化[J].湖北大学学报(自然科学版),2016, 38 (2):142-147.
[10] 姜振芳. 行波型热声发动机的设计及实验研究[D].辽宁:辽宁科技大学,2015.
[11] 隆瑞. 不可逆热力循环分析及低品位能量利用热力系统研究[D].武汉:华中科技大学,2016.
(责任编辑 郭定和)
Optimization of the functionΩof irreversible thermo- acoustic refrigerator
JIANG Zhijie, WU Feng, TIAN Yize
(School of Mechanical & Electrical Engineering,Wuhan Institute of Technology,Wuhan 430073,China)
A cycle model generalized irreversible thermoacoustic refrigerator with complex exponentical heat transfer was built according to thermoacoustic refrigerator of characterstic of oscilation parameter.A mathematical model ofΩ=(2ε-1)R/εwas built.The article analyzed the optimal relationship of each parameter in irreversible thermoacoustic refrigerator by using finite-time thermodynamics in which heat resistance heat leakage and internal dissipation were considered.
thermoacoustic refrigerators; complex index heat transfer; finite-time thermodynamics;optimization
2016-09-12
国家自然科学基金(51176143)资助
蒋智杰(1992-),男,硕士生,E-mail:1119531682@qq.com;吴锋,通信作者,教授,E-mail: wufeng@mail.wit.edu.cn
1000-2375(2017)02-0137-05
TK11
A
10.3969/j.issn.1000-2375.2017.02.006
