平均法在不确定系统稳定性分析中的应用

王培光，候娟娟

(河北大学 数学与信息科学学院,河北 保定 071002)



平均法在不确定系统稳定性分析中的应用

王培光，候娟娟

(河北大学 数学与信息科学学院,河北 保定 071002)

讨论了一类含参数的不确定系统,运用平均法,得到了该系统渐近稳定的结果,并给出了实例验证.

平均法；不确定系统；渐近稳定性

MSC 2000：34D20；34A37

在许多实际工程应用中,几乎所有可运行的系统均要求设计是稳定的,但由于系统自身的复杂性,寻求解析解是十分困难的,因而从理论上探讨解的稳定性是一项有意义的工作.如果一个系统不仅仅依赖于某一时刻的状态,而且还依赖于某种不确定因素,则称该系统为不确定系统[1].Sundarapandian等[2]提出了参数稳定性的概念,并且应用Lyapunov 直接方法分析了不确定参数稳定性问题之后,Ohta等[3]提出了非线性不确定系统平衡位置的稳定性问题,Martynyuk等[4]通过运用不同的Lyapunov函数分析了不确定系统的运动稳定性.这些理论大都运用Lyapunov函数方法讨论不确定系统稳定性问题.

平均法可避免构造Lyapunov 函数带来的困难,Gama等[5]用平均法讨论了右端不连续系统的稳定性问题.本文将平均法应用于不确定系统,得到了不确定参数系统稳定性的充分条件,发展和丰富了不确定系统稳定性理论.

1 预备知识

本文讨论不确定系统

(1)

及其不确定平均系统

(2)

为得到本文主要结果,首先给出如下定义及引理.

定义1[4]称系统(1)在参数α处是参数稳定的,若系统(1)满足下列条件：

A1)存在平衡态xe(α)∈Rn,其中xe:Rd→Rn为向量参数函数,xe=xe(α),α∈Rd;

A2) 对任意的ε>0,存在δ=δ(ε,α)>0,当‖x0-xe(α)‖<δ时,有

‖x(t,α)-xe(α)‖<ε

对任意的t∈R+成立.

定义2[4]称系统(1)在参数α处是参数渐近稳定的,若系统(1)满足下列条件：

A3) 系统(1)在参数α处是参数稳定的；

A4)存在参数β的开领域N(β),对任意的α∈N(β),存在μ(α)>0,当‖x0-xe(α)‖<μ时,有

成立.

引理1 给定η>0,存在ε0>0,使得对任意的ε∈[0,ε0],有{x(t)}⊆{y(t)}+ηB成立.其中B={x∈Rn|‖x‖≤1},{x(t)},{y(t)}分别为系统(1)系统(2)解的集合.

证明：反证法.假设不然,即x(t)∈{x(t)},但x(t){y(t)}+ηB.

令τ2>τ1,那么

(3)

对(3)式两边同时除以τ2-τ1,且两边同时取极限得

(4)

所以存在η>0,系统(1)的解x(t)与系统(2)的解y(t)满足{x(t)}⊆{y(t)}+ηB.

2 主要结果

将运用平均法证明不确定系统与其平均系统解之间的逼近关系,并且进一步证明不确定系统的渐近稳定性.

定理1 假设

(H1)函数f∈C([t0,∞)×Rn×Rd),且满足‖f‖≤M,‖f(s,x(s),α)-f(s,y(s)，β)‖≤λ(‖x(s)-y(s)‖+‖α-β‖),其中λ>0,M为常数,α,β∈S⊆Rd是向量物理参数,d≥1,S是紧集；

(H2)参数α,β满足‖α-β‖≤q,其中q>0为常数.

则对任意的η>0和给定的L>0,存在ε∈(0,ε](ε0=ε0(η,L)),使得对0<ε<ε0,系统(1)的解x(t)与系统(2)的解y(t)满足

‖x(t)-y(t)‖≤η,0≤t≤Lε-1.

证明：首先注意到,(1)的解满足以下积分方程

(5)

且(2)的解满足

(6)

进一步得

(7)

由条件(H1)(H2),有

(8)

令L>0为固定数,对于0≤t≤Lλ-1,有

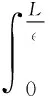
其中

‖f(s,y(s),β)-f0(y(s))‖ds.

并且

进一步得

T2≤2LM.

(9)

再根据(7)和(9)得

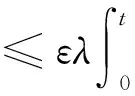
(10)

其中δ=2LM+ελqt.

由引理2,对(10)式应用Gronwall不等式得,

‖x(t)-y(t)‖≤δexp{λL},0≤t≤Lε-1.

更进一步得到

‖x(t)-y(t)‖≤η,t∈[0,Lε-1].

定理1的证明到此完成.

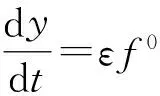
定理2的证明到此完成.

推论1 假设

(H1)函数f∈([t0,∞)×Rn×Rd),且f(t,x,α)是周期为T的周期函数,且满足‖f‖≤M,‖f(s,x(s),α)-f(s,y(s),β)‖≤λ(‖x(s)-y(s)‖+‖α-β‖),其中λ>0为常数α,β∈S⊆Rd, 是2个向量物理参数,d≥1,S是紧集;

(H2)参数α,β满足‖α-β‖≤q,其中q>0为常数,则对任意的η>0和L>0,存在ε∈(0,ε](ε=ε0(η,L)),使得对0<ε<ε0,系统(1)的解x(t)与系统(2)的解y(t)满足

‖x(t)-y(t)‖≤η,0≤t≤Lε-1.

推论1的证明同定理1证明过程类似,不再赘述.

推论2同定理2证明过程类似,不再赘述.

下面举例说明定理的应用,运用平均法分析不确定系统稳定性问题.

3 例子

例1.考虑下列的不确定微分系统

及它的平均微分系统为

[1] 张子方,徐道义.不确定动力系统的稳定性及其应用[D].成都：四川大学, 2004. ZHANG Z F,XU D Y.The stability of uncertain dynamical systems and applications[D].Chengdu:Sichuan University,2004.

[2] SUNDARAPANDIAN V.New results on the parametric stability of nonlinear systems[J].Mathematical and Computer Modelling,2006,43:9-15.DOI:org/10.1016/j.mcm.2005.04.010.

[3] OHTA Y,SILJAK D D.Parametric quadratic stability of uncertain nonlinear systems[J].Systems and Control Letters,1994,22:437-444.DOI:10.1016/0167-6911(94)90087-6.

[4] MARTYNYUK A A,MARTYNYUK-CHERNIENKO Y A.Uncertain dynamical systems:stability and motion control[M].Boca Raton:Taylor and Francis Group,2012.

[5] GAMA R,GUERMAN A,SMIRNOV G.On the asymptotic stability of discontinuous systems analyzed via the averaging method[J].Nonlinear Anal:TMA,2011,74:1513-1522.DOI:10.1016/j.na.2010.10.024.

[6] 葛渭高,李翠哲,王宏洲.常微分方程与边值问题[M].北京：科学出版社,2008.

(责任编辑：孟素兰)

The stability of uncertain systems analyzed via the averaging method

WANG Peiguang,HOU Juanjuan

(College of Mathematics and Information Science,Hebei University,Baoding 071002，China)

The main purpose of this paper is to investigate the asymptotic stability of uncertain systems via the averaging method,and some corresponding results are obtained.We provide an example to illustrate our main results.

averaging method;uncertain systems;asymptotic stability

10.3969/j.issn.1000-1565.2017.01.001

2016-03-01

国家自然科学基金资助项目(11271106)；河北省自然科学基金资助项目(A2013201232)

王培光(1963—)，男，黑龙江哈尔滨人，河北大学教授，博士生导师，主要从事微分方程与控制理论的研究. E-mail:pgwang@hbu.edu.cn

O175.12

A

1000-1565(2017)01-0001-04