露天爆破振动在运输隧道内的传播规律研究

石晨晨，李祥龙，骆浩浩，胡 辉，张晓刚

（1.昆明理工大学 国土资源工程学院，云南 昆明 650093；2.玉溪矿业有限公司狮子山矿，云南 玉溪 651106）

0 引言

金属矿山生产建设中，对井下及地表构筑物进行爆破振动监测，研究爆破振动对构筑物稳定性问题是很重要的。目前我国钨矿山对爆破振动监测研究还不多，因此，该技术推广到钨矿山的生产建设中是非常有意义的。

周建雄[1]通过对现场进行测试，经过理论分析和数值模拟软件计算，分析了爆破地震波对出矿隧道稳定性的影响，并提出具体的隧道支护意见。胡辉[2]对某矿的选厂进行爆破振动监测，得到爆破振动在地表的传播规律，可对地表选厂的稳定性进行评估；安泰龙[3]采用TC4850对爆源周围的隧道进行爆破振动监测，经过线性回归计算，得出爆源附近的爆破振动传播规律，并确定该矿的最大单响药量，推出隧道和爆源的安全距离，为矿山的安全生产提供了保障。史秀志[4]利用爆破振动监测系统对冬瓜山出矿隧道进行振动监测，经过线性回归计算，得到萨道夫斯基公式中的K、α，得到爆破振动有较多主频，但主频较其他频率高，主要振动频率分布范围为100～250 Hz。张力民[5]对矿山生产爆破振动现场进行测试，采用数理统计理论和数值计算方法对不同装药结构条件下的爆破振动速度的变化进行了研究，从计算精度来看，回归分析比数值模拟的精度更高，即回归分析与现场实测吻合度更高。

研究通过对某金属矿山采场进行爆破振动监测，经分析测点Z方向振动速度，得到爆破振动在同一水平运输隧道的传播规律，并利用HHT法对采集的振动数据进行分析，定量分析振动信号传播过程中能量散失的过程，最后给出1230平台、1065平台的最小安全距离。

1 工程概况

某矿山采场位于 102°3′36"E，24°51′48"N[6]。1230、1065平台爆破区域位于81-85号勘探线之间，爆破区域岩性由西向东依次为片岩、夕卡岩、大理岩，爆破区域内节理构造发育，岩石破碎，岩层产状为西倾，有部分水孔。总体岩石坚固性系数f=4.5。

新田进料口西北方向有一条运输隧道叫西帮隧道，距离1065平台西南方向大约410m，距离1230平台西南方向约900m，隧道内运用皮带运输机运输矿石，对西帮隧道进行爆破振动监测，研究爆破振动在西帮隧道内的传播规律对于保障西帮隧道的稳定运输具有重要意义。

2 爆破振动监测

根据《爆破安全规程》（GB6722—2014）[7]爆破振动的判定依据采用测点所在质点Z方向的峰值振动速度和主振频率。监测爆破振动的仪器为TC-4850爆破测振仪和三维速度传感器，速度传感器固定在测点位置，速度传感器通过数据线连接爆破测振仪，测振仪对爆破振动数据进行记录、存储，测振仪通过数据线连接电脑后导出爆破振动数据。

3 爆破振动监测数据与分析

本次爆破振动分为4次进行，第一、三次分别于2017年7月7日、11日1065平台进行生产爆破，第二、四次分为于2017年7月8日、12日1230平台进行生产爆破，在西帮运输隧道布置测点，装药方式为间隔装药和连续装药，采用直线逐孔网络起爆方式，采用磁电雷管起爆，具体爆破参数如表1所示。

测点布置在西帮隧道中，西帮隧道和1230平台、1065平台的大致分布如图1所示。

图1 测点布置图Fig.1 M easuring point layout

3.1 爆破振动监测数据

1230平台、1065平台爆破生产前30min在运输巷道布置测点，待放炮结束一个小时后，收回测振仪，连接电脑导出数据，4次爆破振动数据如表2所示。

表1 1065平台、1230平台爆破参数Tab.1 1065 platform，1230 platform blasting parameter table

表2 爆破振动监测数据Tab.2 Blasting vibrationm onitoring data

3.2 爆破振动信号线性回归分析

在实际工程中，萨道夫斯基公式描述了药量、爆心距、质点振动速度之间的关系，具体见公式（1）所示。

式中：V为爆破振动质点最大速度，cm/s；Q为炸药量，齐发爆破为总药量，延期爆破为最大单响药量，kg；R为爆源距监测点的距离，m；K、α为工程地质条件有关的衰减系数和衰减指数。

将所收集到的数据线性回归后，需要将式（1）转化为线性方程，再进行回归计算。对公式（1）两边同时取以e为底的对数，可得公式（2）。

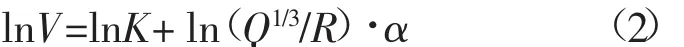
设 y=ln V，a=ln K，b=α，x=ln（Q1/3/R），即可将式可化为标准的线性方程如式（3）所示。

根据爆破振动监测结果，对1065、1230平台测点Z方向上振动速度数据，运用Origin软件对爆破振动数据进行线性回归计算，分析结果如图2所示。

图2 各测点Z方向振动速度的萨道夫斯基公式线性回归图Fig.2 The linear regression of the Sadov's formula for the vibration velocity at each measuring point in Z directionn

依据转化标准线性方程与线性回归图中的方程两者之间对比，再依据所假设的条件推算出与工程地质条件有关的衰减系数K和衰减指数α的值。

即 y=1.892 7x+2.648 3 （R2=0.963 6）

则 K=444.94，α=1.89

得到Z方向的萨道夫斯基振动回归公式为：

3.3 基于HHT方法的爆破振动信号分析

为了更加充分的分析爆破振动波信号，本次采用希尔伯特-黄变换（HHT）算法对爆破振动波形进行时频分析。该程序由EMD法和Hilbert变换两个主要部分组成。EMD方法是HHT法的关键，能够去除干涉波并使波形愈加对称。IMF信号经过EMD方法变换得到，Hilbert变换IMF信号得到瞬时频谱，Hilbert谱可由瞬时频谱综合得到。HHT算法对分析非线性非平稳信号具有较大优势，且具有较强的自主适应性[8-10]。

对1065、1230平台测点爆破振动信号运用HHT法进行时频分析，研究爆破振动在运输隧道内的传播规律。图3为原始波形图，爆破振动持续时间主要分布在0～1 s内，其中，0～0.3 s内爆破振动速度迅速增加，约0.3s时振动速度达到峰值，0.6s后振动速度衰减较快，约1.3 s波形逐渐恢复至初始状态。

图3 原始波形图Fig.3 Original waveform

图4为边际谱，表示每个频率在全局的幅度，次爆破振动频率主要分布在0～30Hz，主频带为15Hz，幅值为1.6×10-6m2·s。图5为能量分布图，表示每个频率在整体时间程度内所积累的能量，其优势频率主要分布在10Hz左右，主要频率范围为0～20Hz，因此，应重点分析0～20Hz区间的爆破振动对运输隧道的影响。

图4 边际谱Fig.4 Marginal spectrum

图5 能量分布图Fig.5 Energy distribution chart

3.4 运输隧道不同距离下的药量控制

随着矿山的持续开采，采场周期性的爆破振动对运输隧道的稳定性造成一定程度的威胁。因此，矿山生产时，相关技术人员给出运输隧道的不同药量下的安全允许距离很有必要。查阅《爆破安全规程》（GB6722—2014）有关爆破振动关于矿山隧道安全允许距离的文献，考虑到运输隧道主要受到约为0～20Hz的爆破振动波的影响，其中，10Hz左右的低频振动波最明显。因此，选取西帮隧道最大安全允许振动速度15 cm/s，通过前面算出的萨道夫斯基公式，可以得到1065平台生产时西帮隧道的最小安全允许距离为33.92m，取35m；1230平台生产时西帮隧道的最小安全允许距离为44.04m，取45m。

为了确保西帮隧道的稳定性，还需要对最大单段药量进行控制，根据已求得的公式其中V取15 cm/s，计算得到公式（4）。

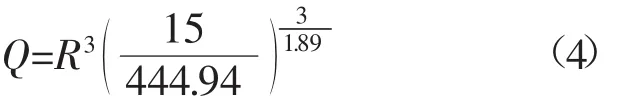
计算不同距离下的最大单段装药量，便于矿山技术人员进行查询，结果如表3所示。

表3 允许最大单段药量控制表Tab.3 Maximum single-paragraph dose safety distance control table

4 结论

（1）1065、1230平台Z方向振动速度萨道夫斯基公式中的衰减系数K=444.94，衰减指数α=1.89，因此，可以根据萨道夫斯基公式描述爆破振动在西帮隧道内的传播规律。

（2）基于HHT方法分析爆破振动在运输隧道内的传播规律，运输隧道受到10Hz左右振动波的影响较大，通过前面算出的萨道夫斯基公式，可以得到1065平台爆破生产时运输隧道的安全允许距离为35m，1230平台爆破生产时运输隧道的安全允许距离为45m。

（3）在运输隧道最大允许振速的条件下，根据爆破振动在运输隧道的传播规律，给出了1230、1065平台爆心距为200～600m范围内的最大单段药量，可指导矿山爆破技术人员现场作业，保证运输隧道安全生产。

[1] 周建雄.爆破地震作用下出矿巷道围岩稳定性分析及控制技术研究[D].长沙：中南大学，2013.ZHOU Jianxiong.Study on stability for surrounding rock of ore drawing roadway and its control techniques under the action of blasting seism[D].Changsha：Central South University，2013.

[2] 胡 辉，李祥龙，石晨晨，等.爆破振动对临近建筑物安全影响研究[J].中国钨业，2017，32（5）：42-48.HU Hui，LI Xianglong，SHI Chenchen，et al.The influence of blasting vibration on the safety of adjacent building[J].China Tungsten Industry，2017，32（5）：42-48.

[3] 安泰龙，李俊孟，齐文跃，等.露天爆破对井工巷道围岩稳定性影响研究[J].煤炭工程，2016，48（1）：74-76，80.AN Tailong，LI Junmeng，QI Wenyue，et al.Study on impact of surface blasting on stability of roadway surrounding rock[J].Coal Engineering，2016，48（1）：74-76，80.

[4] 史秀志，田建军，王怀勇.冬瓜山矿爆破振动测试数据回归与时频分析[J].爆破，2008（2）：77-81.SHI Xiuzhi，TIAN Jianjun，WANG Huaiyong.Blasting vibration measurement regression analysis and time-frequency analysis in Donggua hill mine[J].Blasting，2008（2）：77-81.

[5] 张力民，吕淑然，刘红岩.矿山爆破震动速度的测试与分析[J].矿业研究与开发，2009，29（4）：91-94.ZHANG Limin，LYU Shuran，LIU Hongyan.Test and analysis of velocity of blasting vibration in mine[J].Mining Research and Development，2009，29（4）：91-94.

[6] 赵玉龙.华联锌铟露天采场爆破参数优化及爆破振动在边坡中传播规律的研究[D].昆明：昆明理工大学，2016.ZHAO Yulong.Study on the optimization of blasting parameters and the propagation of blasting vibration in the slope[D].Kunming：Kunming University of Science and Technology，2016.

[7] 中国国家标准化管理委员会.爆破安全规程GB6722—2014[S].北京：中国标准出版社，2014.

[8] 龚 敏，邱燚可可，孟祥栋，等.基于HHT的雷管实际延时识别法在城市环境微差爆破中的应用 [J].振动与冲击，2015，34（10）：206-212.GONG Min，QIU Yikeke，MENG Xiangdong，et al.Identification method of detonator's actual firing time delay based on HHT and its application in millisecond blasting under urban environment[J].Journal of Vibration and Shock，2015，34（10）：206-212.

[9] 宋文峰，张 琪，李跃中，等.基于HHT爆破地震波穿越岩体层面衰减规律研究[J].爆破，2015，32（4）：153-157.SONG Wenfeng，ZHANG Qi，LI Yuezhong，et al.Study on attenuation law of blasting seismic waves through rock layers based on HHT[J].Blasting，2015，32（4）：153-157.

[10] 邱贤阳，史秀志，周 健，等.基于HHT能量谱的高精度雷管短微差爆破降振效果分析[J].爆炸与冲击，2017，37（1）：107-113.QIU Xianyang，SHI Xiuzhi，ZHOU Jian，et al.On vibration reduction effect of short millisecond blasting by high-precision detonator based on HHT energy spectrum[J].Explosion and Shock Waves，2017，37（1）：107-113.