拉格朗日中值定理的教学设计
2017-03-13赵萨日娜
赵萨日娜
(吉林省经济管理干部学院,吉林长春 130000)
1 教学背景
学生通过前期教学,对于学习本节课的相关知识基础而言,基本掌握了直线的斜率公式、直线的方程、函数的连续性及闭区间上连续函数图像的特点、导数的几何意义和基本求导公式。学生的逆向思维、创造思维、逻辑思维能力有待进一步开发和锻炼。
2 教学目标
通过本课教学使学生理解拉格朗日中值定理及其几何解释;了解构造辅助函数的思想方法和用罗尔定理证明拉格朗日定理的方法;掌握罗尔定理与拉格朗日定理的关系。从而达到锻炼学生逆向思维、创造思维、逻辑思维的目的。
3 教学方法
主要采用讲授法、数形结合法、启发式教学等。
4 教学内容
4.1 罗尔定理及其几何意义
若函数 f(x)满足:(1)闭区间[a,b]上连续;(2)开区间(a,b)内可导;(3)f(a)=f(b),则在开区间(a,b)内至少存在一点 ξ,使得 f′(ξ)=0。 其几何意义如(图 1):在端点同高的连续光滑曲线弧AB上至少有一点C,在该点处的切线是水平的。
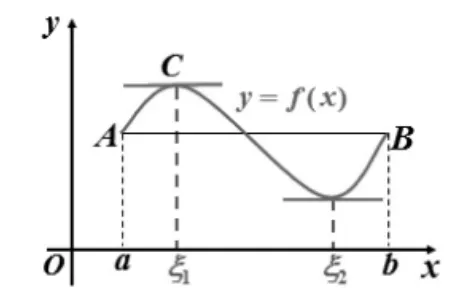
图1
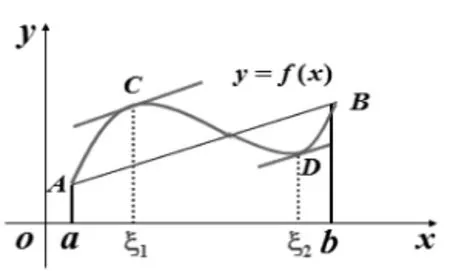
图2
4.2 拉格朗日定理的引出
指出定理中条件(3)f(a)=)f(b)较为苛刻,提出若去掉此条件,即,将图1倾斜一定的角度观察,会产生什么结论?从而引出拉格朗日中值定理。
注意,先让学生独立思考两分钟,然后提问学生,引导其从几何图形的变化入手得到新结论:即如图2拉格朗日定理的几何解释——连续光滑曲线弧AB上至少有一点C,在该点处的切线是平行于弦AB的。
再根据几何解释得到其内在的数量关系:
若函数 f(x)满足:(1)闭区间[a,b]上连续;(2)开区间(a,b)内可导,则在开区间(a,b)内至少存在一点ξ,使得
4.3 拉格朗日定理的证明
思路:构造辅助函数g(x),要求其满足罗尔定理条件,尤其是 g(a)=g(b)…(1),同时由罗尔定理结论能使
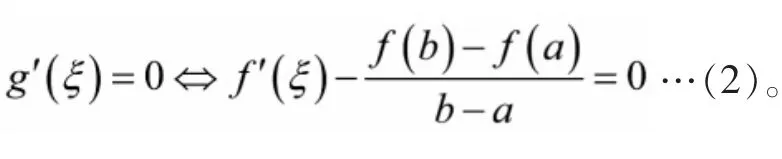
证明的关键是构造辅助函数,方法很多,主要借助逆向思维、创造思维.这里介绍两种典型方法。
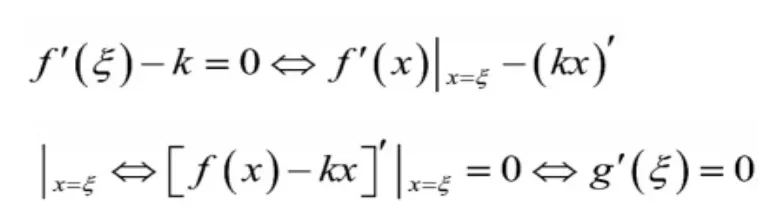
因此,可构造辅助函数,
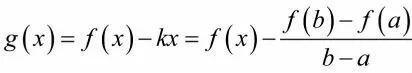
已知有g(a)=g(b),满足辅助函数的两个要求。由罗尔定理证得拉格朗日定理。
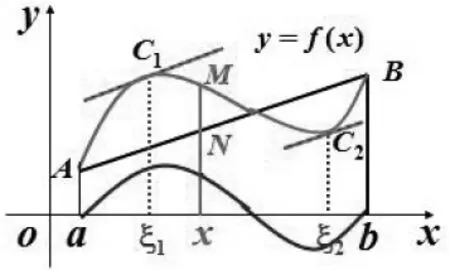
图3
如图3,由弧AB与弦AB端点重合的特点,试取处,其对应的弧AB上点M与 弦AB上点N的纵坐标之差为辅助函数:
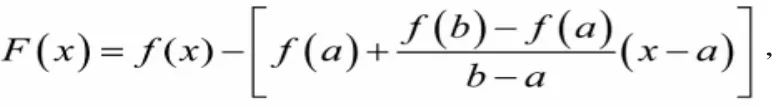
则有 F(a)=F(b)=0 且
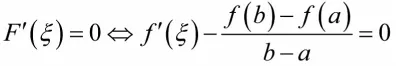
满足了构造辅助函数的两个要求。于是由罗尔定理,稍加整理证得拉格朗日定理。
4.4 拉格朗日定理的应用举例
应用拉格朗日中值定理推得了用函数在区间上一阶导数符号判断函数的单调性的方法。
应用拉格朗日中值定理推得了函数在某区间上一阶导数恒为零,则此函数在此区间上是常数。
例 1:设不恒为常数的函数 f(x)在[a,b]上连续,在(a,b)内可导,且 f(a)=f(b)。 试证在开区间(a,b)内至少存在一点 ξ,使得 f(ξ)>0。
分析:依题设可知f(x)在[a,b]上满足罗尔定理条件,而结论为导函数在某点处的值大于零,因此不能用罗尔定理,可设想,如果能利用拉格朗日中值定理,而 f(x2)-f(x1)与 x2-x1同号,则命题可证。为此构造区间。
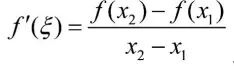
证:因为 f(a)=f(b),且 f(x)不为常数,因此至少存在一点 c∈(a,b),使得 f(c)≠f(a)=f(b)。不妨设 f(c)>f(a),在[a,c]上f(x)满足拉格朗日中值定理条件,故至少存在一点,使由于 f(c)>f(a),c>a,可知 f′(ξ)>0,证毕。
5 教学小结
在现如今高等数学教学越发的讲究实用主义教学的大环境下,为使学生更多地领悟数学的精神实质和思想方法,使学生自觉地接受数学文化的熏陶,讲清楚一些经典的、重要定义、定理的来龙去脉是非常必要的,尤其应该讲清楚逻辑证明的思路及过程,使学生体会严密有理、丝丝入扣的数学逻辑之美。
[1]张泽林.关于拉格朗日(Lagrange)中值定理的教学设计[J].咸宁学院学报,2005(6):24-26.
[2]黄强联,朱兰萍.关于Lagrange中值定理的逆命题[J].高等数学研究,2012,15(5):15-16.
[3]刘三阳,杨国平.关于Lagrange中值定理的反问题[J].高等数学研究,2007(5):40-41.
