思维比对理念下试卷分析课的教学研究

姜群星

（浙江省淳安县威坪中学，浙江淳安 311715）

1 选题由来

1.1 试卷分析课中的现状

在我们教学实践中，很多教师对试卷分析并不十分重视，很少有教师认真去备一下试卷分析课。很少有教师为了一堂试卷分析课而精心写好教案：教学目标、教学流程、教学方法、教学手段、教具准备、设计实验、媒体选择、板书设计、检测试题等课堂教学的要件。而多数教师都以对答案为教学主线，以学生错得较多的试题分析讲解为主要内容，以教师讲学生听为主要形式。尤其是在毕业班进行试卷分析时情况更糟：课代表报答案或把答案抄在黑板上，学生自行改正，有问题的同学向教师提问。因为毕业班的教师批改任务繁重，根本没有时间去备试卷分析课。据笔者观察，也没有哪位领导愿意听试卷分析课，没有开展过有关试卷分析课的教研活动，试卷分析的公开课、观摩课，所有这些现象都表明，试卷分析课——一个被遗忘的角落。

1.2 试卷分析的作用

（1）具有评价功能。考试对学生的“学”和教师的“教”具有重要的指向作用。许多教师在平时考试中，常常只对分数评价感兴趣，而很少对考试题目的解答方法与卷面得失原因进行深入分析，造成对教学有益的考试信息的流失，也因此使考试的作用与功能下降。因此，应当把考试看作是评价教学质量和教学效果的重要手段。使教师能够从考试卷面分析中得到改进措施，让学生从卷面分析中找到存在的问题及薄弱环节，以利于学生改进学习方法，提高学习成绩。

（2）具有反馈功能。通过考试卷面的分析，可以为教与学提供反馈信息，就能促使教师改进教学方法，来提高教学效果，同时试卷分析也能为学生改进学习方法提供指导。但是要求对试卷的分析必须建立在正确、客观的基础上，这样才能为师生反馈真实有用的信息。由此可见，改进现有的试卷分析弊端，提高试卷分析课的有效性，使之成为提高教学质量的重要手段，对于推进新课程改革、促进教师专业发展都具有重要的现实意义。

2 试卷分析的类型

根据考试的目的不同可以把试卷分析分为两大类型：一是专业调研型试卷分析；二是常态试卷分析。本文将重点探讨常态试卷分析课。

所谓常态试卷分析，主要是指教学常规中的期中、期终考试、每一章的单元考试等。这一类试卷分析是教师教学的常规工作和常态工作，但又是教师重点应对的一类试卷分析工作，是本文探讨的主要内容。笔者在本文中想探讨的问题旨在这一类试卷分析中如何有所突破、有所创新、有所成效。

一般地说，试卷分析课的常态功能主要有：一是对答案，把错的改正过来；二是对错得较多的问题进行重点讲解；三是发现教学中的疏漏过失；四是诊断学生还存在哪些未解决的问题。

2.1 从宏观层面来分析

一是，对考试要点进行评析。主要是对重点、难点知识、易错易忘知识点的分析。通过这样的分析就能让学生产生深刻的记忆效果，由于考试本身就是为了让学生检查对知识的掌握情况，对过卷面分析既能复习旧知识，又能对掌握不牢固的问题加深记忆。进行试卷评析时，要让学生借机对所学知识进行系统自习。因此，进行试卷分析课教学，老师需要考虑讲课的重点所在。

案例1：抛物线y2=4x的焦点为F,A、B、C是其上的三点，若的值。

分析：题中涉及向量和、长度和，可联想到向量的坐标运算、距离公式及几何意义等。

具体解法探究如下：

探究 1：设出三点的坐标为 A(x1，y1)、B(x2，y2)、C(x3，y3)，由，可得 x1+x2+x3=3

思路1：通过运用两点间距离公式并化简，利用x1+x2+x3=3可求值。

探究2：分析上述解法，发现利用抛物线上的“三点”满足的向量关系，可得到数量关系x1+x2+x3=3，从而求出长度之和。

思考：四点与三点的问题的解法是一致的，改成更多的n个点呢？

结论1：抛物线y2=4x换成一般的形式，y2=2px(p＞0)的焦点为 F，A1，A2，A3，…，An是其上的 n 个点，若的值为np。

拓展2：上述研究过程中，涉及焦点，准线及焦半径的关系，那么同样具备这几个元素的椭圆和双曲线是否有类似的结论？

通过对试卷中的经典题目进行纵向推广、横向发展的深入研究，寻求解决一类问题。促使学生积极思维、勇于探索，使学生认识问题的水平和思维能力得到提升。对于考试题目来说，试卷的每一个题目都可以作为讲解内容，不能仅以所占的分数多少来作为讲解的依据，每一类知识都要照顾到，但也不可能面面俱到，每次的讲评要有所侧重。

二是，对学生失分最多的题目进行分析。通过考试，肯定能够发现许多问题，进行试卷分析应把重点放在帮助学生找到学习中存在问题，以及造成问题的原因，包括解题方法、思维方法、基本知识的掌握情况等，应把这些内容作为讲评重点。

案例2：若化简|1-x|-|x-4|的结果为2x-5，求x的取值范围。

分析：（1）原式=|1-x|-|x-4|根据题意，要化成：x-1-（4-x）=2x-5，从绝对值概念的反方向考虑，推出其条件是：1-x≤0，且 x-4≤0，所以 x 的取值范围是：1≤x≤4。

（2）本题得分率较低，究其原因，是学生不能运用逆向思维方法。本题的另一种解法是先找出绝对值的零点：x=1 或 x=4，然后按 x＜1,1≤x≤4,x＞4 分类讨论去掉绝对值，化简后与结果比较，得到x的取值范围。通过分析试卷，找出问题的原因，才能让学生有所改进。

三是，注重试卷分析的方法。进行试卷分析课，老师要注重讲课的方式方法，讲解中可以把老师的解题方法进行讲解，也可以把学生中好的解题方法进行展示，还可以把全班学生对每个重点题目的解题方法全部列出来，让学生进行比较、选择，可增强学生解题的灵活性。

分析：本题旨在考查函数的性质，不少学生忽略了函数f(x)的定义域这个前提条件，从而导致错误。通过学生答题中各种方法的展示，并让学生进行对比、讨论和交流。

总之，试卷分析课也要有一定的教学方法，明确的教学目标，清晰的教学程序安排。这样才能收到更好的效果。

2.2 从微观层面分析

试卷分析应重视思维的三比对。所谓思维比对主要是指考试后通过试卷分析、错因探究、错题订正、评价交流后所提升的思维水平与考试时自己的思维水平进行比对。

（1）考时与考后的思维比对——思维的纵向比对。

首先是对于错题要启发学生针对听了教师的讲解后，要进行考前与考后的思维比对。即考试时自己是如何理解、处理试题的？而现在有无新的感悟？

其次是对已经得分的试题，现在有无想到还有更简明、快捷的方法开展思维比对。

表1

当a增大时：

A.E(η）增大，D(η)增大 B.E（η）减小，D（η）增大

C.E(η)增大，D(η)减小 D.E(η)减小，D(η)减小

以上两种方法在求方差的时候计算较繁。

方法3：当a增大时，-1对应的概率变大，0对应的概率变小，而1对应概率不变，可以得到离散数据波动大，反之则离散数据波动小，所以a增大则D（η）增大。从方差的定义去解题就可以很快求得答案。

其中第三种方法可谓干净利落，令人拍案叫绝。

（2）考生与他生的思维比对——思维的横向比对。

由于新课程理念提倡探究式学习，因此，在试卷分析课中，第一个环节应该让学生分小组针对试卷上各自的问题进行广泛的讨论与交流，使一些简单问题、错因不复杂的问题在小组内就能得到解决。

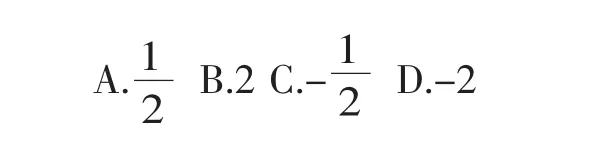
这是一道基础题，学生容易想到。

（3）学生与教师的思维比对——思维的交叉比对。

在试卷分析中，既要充分体现学生的主体作用，也要发挥教师的主导作用。可以说，教师的思维方法和思维品质对学生会产生极大的影响。尤其是对那些学生解起来感到困惑不解的问题，更应该发挥教师的示范作用，使学生有一个明确而清晰的思维比对。

总之，试卷分析课的设计要有利于培养学生的思维能力。通过试卷分析要使学生有一个思维的参照，知道自己的对错与优劣；明白自己解法的正误与简繁；悟出自己解题犯错的原因与误判缘由。因此，需要教师给予足够重视。

[1]唐松锦.中考数学创新性试题分析与命题研究[D].广州大学,2011.

[2]王林全，林国泰.中学数学思想方法概论[M].广州：暨南大学出版社，2000.

[3]蔡德清.中考数学压轴题的命题研究与反思[J].福建中学数学,2010(11):11-14.