题干中含有“至少”的关系代数查询问题探讨
2017-03-13程晨
摘 要 本文结合笔者多年的教学研究和实践对关系代数查询题干中含有“至少”的这样一类查询问题进行了阐述和探讨,希望能够对该类问题教学研究的发展有所帮助。
关键词 关系代数 “连接”运算 “除”运算 “至少”
中图分类号:O15 文献标识码:A DOI:10.16400/j.cnki.kjdkz.2017.01.028
An Approach to the Problem of Algebra Query with the "Least" in the Problem
CHENG Chen
(School of Computer Science and Technology, Nantong University, Nantong, Jiangsu 226019)
Abstract This paper combined of teaching research and practice of the author's stem contains described and discussed in such a class of queries “at least" query of relational algebra, hoping to help the development of teaching and research of this kind of problem.
Keywords relational algebra; connection operation; "removal" operation; “least”
1 关系代数概述
关系数据语言可以分为三类:关系代数、关系演算、既具有关系代数的特点又具有关系演算特点的语言(主要指SQL)。其中关系代数是用对关系的运算来表达查询的。关系代数共有八种运算,按照运算方向的不同可以分为两类:集合运算和专门运算。集合运算包括并、交、差、笛卡尔积,这类运算把关系看成是元组的集合,运算方向是元组的方向;专门运算包括选择、投影、连接、除。这类运算不仅涉及到元组的方向,还有可能涉及到属性列的方向。按照是否可以由其它关系运算导出,关系代数的八种运算也可以分为两类:基本的关系运算和非基本的关系运算。基本的关系运算包括:并、差、笛卡尔积、选择、投影;非基本的关系运算包括:交、连接、除。
2关系“连接”运算
连接运算属于非基本的关系运算,连接运算的本质相当于笛卡尔积+选择。两个表进行连接运算,相当于先对两个表进行笛卡尔积运算,然后对于笛卡尔积的结果施加某些条件进行选择运算,最终得到连接运算的结果。按照选择的条件中的比较运算符是否为等号可以将连接运算分为两类:当比较运算符为等号时称为等值连接,不是等号时称为非等值连接。在等值连接中又有一种特殊的连接称为自然连接:当两个表具有公共属性组,并且在结果中取消重复列的等值连接称为自然连接。在具体查询中用到的连接大部分都是自然连接。
3关系“除”运算
关系除运算也属于非基本的关系运算。两个关系进行除运算,要求两个关系具有公共属性组。假设两个关系为A(P,Q)和B(Q,R),Q即为公共属性组。A和B的除运算的结果是一个新的关系C(P),C是A中满足以下条件的元组在P属性组上的投影,元组在P上分量值p的象集包含B在Q上的投影。除运算在所有的关系运算中是最难的一种。
4 题干中含有“至少”的关系代数查询问题的分析和解决
有这样一类关系代数的查询,其查询的题干里含有“至少”这样一个关键词。对于这样一类查询问题,原则上可以考虑用除运算来解决。但是否一定用到除运算,则还要考虑是否有“确定的包含关系”,因为除运算的概念里其实就有“确定的包含关系”。于是可以把这样一类查询问题又细分为两类:确定的包含关系、不确定的包含关系。
4.1 確定的包含关系
确定的包含关系需要使用除运算,下面举三个实例加以说明。在以下的关系数据库中查询至少选修了读者编号为“13050220”的读者所借阅过的全部图书的读者的读者编号、姓名、部门。
图书(书号,书名,作者,出版社,类别,定价)
读者(读者编号,姓名,性别,年龄,部门)
借阅(书号,读者编号,借阅日期,归还日期)
上述查询里有确定的包含关系:设该读者所借阅图书的图书号所构成的集合为集合1,读者编号为“13050220”的读者所借阅过的图书的图书号所构成的集合为集合2,如果集合1包含了集合2,则就说明该读者至少选修了读者编号为“13050220”的读者所借阅过的全部图书。很显然,上述的集合1和集合2都是确定的集合,所以此查询要用到除运算。
表式: 读者编号,书号(借阅)€鳌∈楹牛ā《琳弑嗪?‘13050220(借阅))∞ 读者编号,姓名,部门(读者)
在以下的关系数据库中查询至少用了供应商S1所供应的全部零件的工程号。
供应商(供应商编号,供应商姓名,供应商所在城市)
零件(零件编号,零件名称,颜色,重量)
工程(工程编号,工程名称,工程所在城市)
供应(供应商编号,零件编号,工程编号,数量)
上述查询里有确定的包含关系:设该工程所使用的零件编号及其供应商编号所构成的集合为集合1(此集合的每个元素都包含了零件编号、供应商编号这两个属性),供应商S1所供应的零件编号及其供应商编号所构成的集合为集合2(此集合的每个元素也都包含了零件编号、供应商编号这两个属性,只不过供应商编号的取值均为S1),如果集合1包含了集合2,则就说明该工程至少用了供应商S1所供应的全部零件。很显然,上述的集合1和集合2都是确定的集合,所以此查询要用到除运算。
表达式为: 工程编号,供应商编号,零件编号(供应)€鳌」┯ι瘫嗪牛慵嗪牛ā」┯ι瘫嗪?‘S1(供应))
在以下的关系数据庫中查询至少参加了项目编号为2、3、5号的雇员的信息(所有属性)。
雇员(雇员编号,姓名,性别,年龄,部门)
项目(项目编号,名称,经费,起始时间,终止时间)
参加(雇员编号,项目编号,相应职责)
上述查询里有确定的包含关系:设该雇员所参加的项目的项目编号所构成的集合为集合1,2、3、5这三个项目编号所构成的集合为集合2,如果集合1包含了集合2,则就说明该雇员至少参加了项目编号为2、3、5号的这三个项目。很显然,上述的集合1和集合2都是确定的集合,所以此查询要用到除运算。
表达式为 雇员编号,项目编号(参加)€鳌∠钅勘嗪牛ㄏ钅勘嗪?‘2v项目编号=‘3v项目编号=‘5(项目))∞雇员
4.2 不确定的包含关系
不确定的包含关系不能使用除运算,下面举三个实例加以说明。在以下的关系数据库中查询至少选修了其先修课为7号课程的学生的学号。
学生(学号,姓名,性别,年龄,院系)
课程(课程号,课程名,先修课,学分)
选修(学号,课程号,成绩)
上述查询里的包含是不确定的:假定1、2、3号课程的先修课均为7号课程。设该学生所选修的课程的课程号所构成的集合为集合1,那么集合2并不是一个确定的集合,以下的集合:{1}、{2}、{3}、{1,2}、{1,3}、{2,3}、{1,2,3},当集合1包含上述集合时,均符合此查询的要求。因此本查询的包含是不确定的,不需要使用除运算。
本查询使用三个关系的连接即可,表达式: 学号( 先修课=‘7(学生∞选修∞课程))
在以下的关系数据库中查询至少参加了两个项目的雇员的雇员编号、姓名、部门。
雇员(雇员编号,姓名,性别,年龄,部门)
项目(项目编号,名称,经费,起始时间,终止时间)
参加(雇员编号,项目编号,相应职责)
显然以上的查询是不确定的包含:至少参加了两个项目,意思是参加了两个,或者参加了三个,或者参加了四个等等;即使就是参加了两个,到底是哪两个,也是不确定的。所以此查询不能使用除运算。
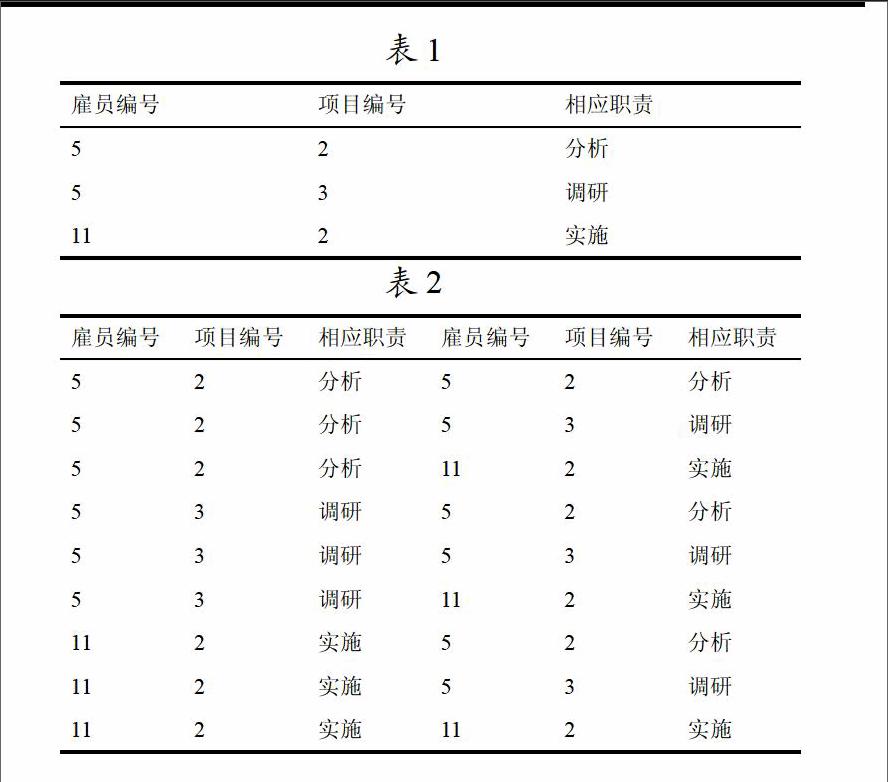
此查询需要把两个“参加”关系“拼接”起来,但是此种“拼接”不能使用自然连接,因为自然连接会取消重复的属性列,应该使用笛卡尔积把两个“参加”关系拼接起来。假设“参加”关系如表1所示,则参加参加如表2所示。
在“参加”关系中,雇员编号为“5”的雇员至少参加了两个项目(正好两个),而雇员编号为“11”的雇员只参加了一个项目。在参加参加关系中,至少存在一个元组,第一列的雇员编号取值和第四列的雇员编号取值相等,都等于“5”;而第二列的项目编号取值和第五列的项目编号取值不相等,一个取值为“2”,另一个取值为“3”。在参加参加关系中,不存在这样一个元组:第一列的雇员编号取值和第四列的雇员编号取值相等,都等于“11”;而第二列的项目编号取值和第五列的项目编号取值不相等。因此由上述所分析的条件使用选择运算先求出至少参加了两个项目的雇员的雇员编号,然后再和“雇员”关系自然连接求出姓名、部门。
此查询的表达式为: 1( 1=4∧2<>5(参加€撞渭樱蕖?,2,5(雇员),表达式用序号来表示相应的属性列。
在以下的关系数据库中查询至少借阅过一本类别为天文类图书的读者的信息(全部属性)。
图书(书号,书名,作者,出版社,类别,定价)
读者(读者编号,姓名,性别,年龄,部门)
借阅(书号,读者编号,借阅日期,归还日期)
上述查询中虽然有“至少”,但同时也有数字“一”,这种类型查询里的包含往往也是不确定的:假定天文类图书有四本,书号分别为6、7、8、9。设该读者所借阅的图书的书号所构成的集合为集合1,那么集合2并不是一个确定的集合,以下的这些集合:{6}、{7}、{8}、{9}、{6,7}、{7,8}、{8,9}、{6、7,8}、{7、8,9}、{6、7、8、9}等等,当集合1包含上述集合时,均符合此查询的要求。因此本查询的包含是不确定的,不需要使用除运算。
这种类型的查询直接使用自然连接,表达式如下:
读者编号,姓名,性别,年龄,部门( 类别=‘天文(图书∞借阅∞读者))
5 结束语
关系代数的查询问题有这样一类,其题干中含有“至少”这样一个关键词,笔者根据多年的教学经验将这样的一类查询问题分为两类:确定的包含关系和不确定的包含关系,前者需要使用关系除运算,后者不能使用关系除运算,需要考虑诸如自然连接甚至是传统的集合运算等其它关系运算。
南通大学教学改革课题《数据库原理及应用》 课程上机实验教学改革及质量评价指标体系的研究与实践(2015B55)
参考文献
[1] 王珊,萨师煊.数据库系统概论(第五版)[M].北京:高等教育出版社,2014.
[2] 程晨.数据库原理课程中关系代数除运算教学的探讨[J].电脑知识与技术,2014(14):3338-3339.
