FEM/SPH耦合方法在鱼雷入水研究中的应用

张岳青, 蔡卫军, 李建辰, 王志杰



FEM/SPH耦合方法在鱼雷入水研究中的应用

张岳青, 蔡卫军, 李建辰, 王志杰

(中国船舶重工集团公司第705研究所, 陕西西安, 710077)

为了扩大鱼雷浅海区的使用范围, 浅水控制技术非常重要, 鱼雷入水过程的非定常运动参数是初始控制的输入条件。文中采用有限元/光滑粒子流体动力学(FEM/SPH)耦合方法, 建立鱼雷入水仿真模型, 对鱼雷从触水到全沾湿过程进行了数值仿真, 仿真结果与试验数据吻合较好, 说明FEM/SPH耦合方法对于入水问题的研究具有明显的优势。仿真分析了鱼雷入水过程中运动姿态的变化, 以及入水冲击加速度的变化趋势, 文中所做研究为进一步研究鱼雷入水问题提供参考。

鱼雷入水; FEM/SPH耦合方法; 非定常参数

0 引言

我国海域辽阔, 领海主权受到各个方面的威胁和挑战, 鱼雷作为海军主要作战武器, 在现代和未来海战中的地位不可替代。针对我国多数海域水深较浅的状况, 提高鱼雷的浅水控制技术, 以扩大鱼雷在浅水区的使用范围势在必行。目前, 鱼雷可以通过火箭助飞、飞机空投和水面舰艇等多种方式进行发射, 发射后鱼雷都会经历一个入水过程。而在鱼雷侵水过程中是无法进行控制的, 只有待到其全沾湿后, 控制系统才能对鱼雷运动姿态进行有效控制, 所以鱼雷全沾湿时的速度、深度、滚动角、俯仰角和偏航角等运动参数是鱼雷浅水控制的输入条件。鱼雷从触水到全沾湿的侵水过程非常复杂, 如果能准确的对此过程进行仿真分析, 获得鱼雷全沾湿时的运动参数, 对鱼雷浅水控制深度非常重要。

鱼雷入水过程涉及固体、液体和气体3种介质的运动, 力学环境极为复杂。在整个入水过程中, 雷体的运动、水的运动、空泡内的气体运动都具有强烈的非定常性, 入水冲击载荷可能造成雷体和雷内部件的变形或者破坏, 同时对鱼雷入水弹道产生重要的影响, 使鱼雷入水时发生翻转和冒水等危险运动[1]。

对于入水问题, Von Karman[2]于1929年最早提出入水理论, 采用附加质量法计算水上飞机降落过程中的入水冲击载荷。1932年, Wagner[3]考虑到结构在冲击过程中的液面抬升现象, 提出了小斜升角模型的近似平板理论, 成为对结构入水冲击理论研究的基础。基于二人研究基础, 研究者针对简单结构的入水问题进行了理论、试验和数值仿真等方面的研究, 并取得了很多成果[4-6]。近年来, 国内针对鱼雷入水问题的研究相对较少。1990年, 严忠汉[7]采用固化系数法对鱼雷三自由度纵向姿态运动进行了分析, 得出了入水鱼雷带空泡航行保持姿态运动稳定的条件, 提出入水鱼雷尾部稳定器设计原理思想。1998年, 颜开等[8]采用Mackey方法, 根据实验空泡的外形, 重新拟合了空泡椭球模型中的经验常数, 分析了由雷体与空泡壁的相互作用引起的鱼雷流体动力变化特性, 计算预报的入水弹道与模型试验结果吻合得较好。2009年, 潘光等[9]研究了高空远程滑翔鱼雷的全弹道, 分析了各阶段弹道的主要特点。2011年, 安伟光等[10]依据气体泄漏规则建立起空泡深水闭合后空泡内气体平衡方程, 分析运动体入水及带空泡航行的受力特性。空泡内气体的弹性对计算结果有很大的影响。2015年, 邬明[11]在考虑入水空泡的基础上, 采用Matlab求解了航行器带空泡航行阶段的流体动力, 分析了航行体入水深度、姿态和速度随时间的变化。朱珠等[12]基于CFD计算获得了柱体大攻角入水过程流体动力特性, 建立了大攻角入水弹道模型, 仿真分析了入水攻角和速度对入水弹道的影响规律。

目前针对鱼雷入水问题的仿真, 多数采用有网格方法, 由于网格的局限性, 对鱼雷入水运动特性研究中极易造成网格畸变, 致使计算精度不高, 甚至无法进行计算。文中基于无网格方法的优势, 采用有限元方法(finite element method, FEM)和光滑粒子流体动力学(smoothed particle hydrodynamics, SPH)耦合方法, 对鱼雷从触水到全沾湿整个过程进行了仿真, 研究了鱼雷入水过程中的冲击加速度和入水初始段鱼雷姿态的变化。

1 FEM/SPH耦合方法

FEM/SPH耦合方法是将FEM和SPH耦合起来, 发挥2种方法各自的优势, 针对大变形问题进行仿真计算的方法。FEM方法在计算连续介质的力学变形问题时, 具有更高的效率和准确度; SPH方法基于无网格的特点, 在模拟大变形、不连续介质动力问题时具有较大优势。因此针对鱼雷入水问题的仿真, 鱼雷变形很小, 采用FEM方法; 水由于冲击作用变形很大, 采用SPH方法。此方法能在保证精度与准确性的同时提高计算效率。

1.1 SPH方法基本理论

SPH方法不需要生成网格, 是一种纯粹的Lagrange粒子方法, 将水的计算域离散成有限数量的粒子(见图1), 每个粒子上都拥有一系列参量信息, 如水的密度、速度和能量等。初始状态下, 不需要定义各个粒子之间的关联性, 整个计算域中水粒子的变化过程需要质量、动量和能量守恒定律进行控制, 所以在SPH方法中首先需要将基本控制方程进行离散化处理。

SPH方法所基于的基础理论是插值理论, 首先需要将偏微分方程采用核近似方法转换成积分方程, 然后采用粒子近似法将积分方程进行离散化, 形式离散化的粒子方程。由此, 可以理解核函数近似法是SPH方法的核心思想之一[13]。

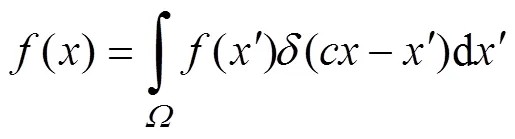
(2)

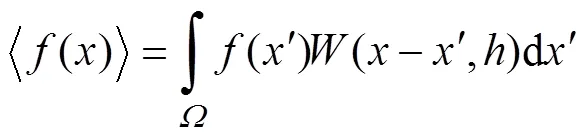
1) 正则化条件

2) 当光滑长度趋向于零时具有狄拉克函数性质

(5)

3) 紧支性条件

3次B样条函数是SPH方法中最常用的光滑函数, 其表达式

最后, 将函数积分表达式进行离散化, 由支持域内有限个粒子的和形式来表示。离散化后, 粒子的表达式为

(9)

式(8)经粒子离散后, 转化为

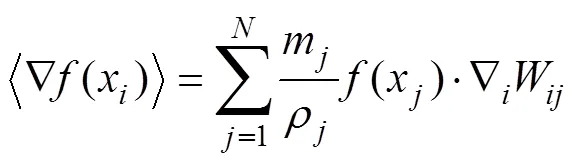
由此, 对基本方程进行离散, 可以得到SPH方法的离散化的控制方程

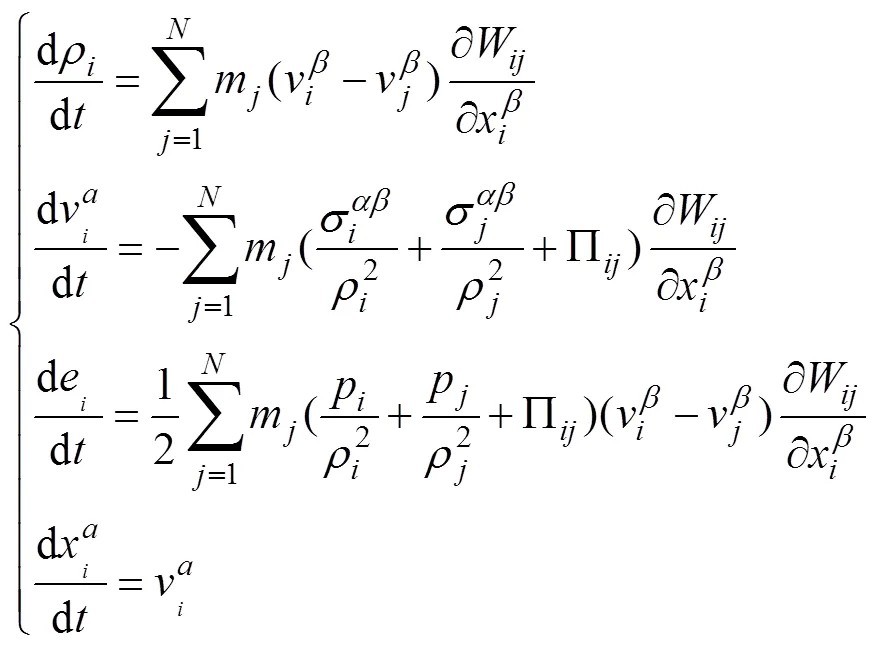
1.2 界面耦合算法

在鱼雷入水过程中, 实现鱼雷和水2种介质相互作用, 需要在FEM/SPH耦合方法中, 将网格和粒子之间的界面进行处理。鱼雷网格和水粒子之间需要采用接触算法进行相应的计算处理。

图2为鱼雷网格和水粒子之间的接触面。网格节点S1, S2, S3和S4之间的连线为2种介质之间的接触面。粒子半径

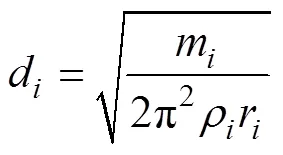
图2 有限元(FEM)网格与SPH粒子接触面

Fig. 2 Interface between FEM(finite element method) mesh and SPH particle

其中接触面处的法向接触力表达式为

接触面切向接触力表达式

2 仿真模型

针对鱼雷入水冲击的特点, 鱼雷变形很小, 重点关注鱼雷入水过程中的姿态变化, 所以鱼雷采用FEM网格, 材料模型选用刚体模型, 实现鱼雷质心、质量、转动惯量、入水角度和速度的仿真, 完成鱼雷多自由度运动; 冲击过程中会造成水的飞溅, 变形较大, 所以水采用SPH粒子, 材料模型选用NULL材料模型和Gruneisen状态方程; 在整个计算域通过施加体力的方式实现重力场的模拟, 仿真模型和坐标如图3所示。鱼雷入水参数范围如下: 入水角度为1º~20º,方向入水速度为15~25 m/s,方向入水速度为–5 ~ –10 m/s, 入水初始俯仰角速度为–10~–20 (º)/s。选取其中的典型工况, 入水角度为16º, 入水速度为20 m/s, 入水初始俯仰角度为14 (º)/s。对仿真结果(cal)和试验数据(exp)进行了对比分析。

3 仿真分析

3.1 入水过程

鱼雷入水过程如图4所示。

0.05 s时, 鱼雷入水点处水面发生飞溅, 雷头侵入水中; 0.15 s时, 鱼雷质心没入水面之下, 水面飞溅更加明显, 鱼雷上部形成明显空腔; 0.25 s时, 鱼雷上部空腔逐渐增大, 鱼雷雷尾没入水中; 0.4 s时, 鱼雷受到侵水力矩作用, 顺时针方向旋转, 俯仰角逐渐增大, 雷尾空腔逐渐减小; 0.5 s时, 鱼雷入水后形成的空腔基本闭合, 雷体趋于全沾湿, 在水的阻力作用下, 鱼雷速度已变得较小; 0.6 s时, 水面溅水在重力作用下逐渐回落, 鱼雷运动状态基本稳定。

3.2 俯仰角速度和俯仰角

鱼雷入水时俯仰角速度的变化对鱼雷后续姿态的影响较大。从鱼雷入水后俯仰角速度(见图5)和俯仰角(见图6)的无量纲变化曲线可以看出, 仿真值和试验值变化比较一致, 说明数值仿真的鱼雷入水姿态与试验中鱼雷姿态变化也是一致的。鱼雷入水后, 俯仰角速度负方向迅速增大, 说明鱼雷入水后受到“低头”力矩的作用, 俯仰角持续增大。到0.035 s时俯仰角速度值有所减小, 并持续减小了约0.02 s, 由图4知, 此时鱼雷处于雷头侵水过程中。0.055 s时, 雷头已没入水中, 低头力矩持续作用, 俯仰角速度和俯仰角继续负向增大。0.1 s后俯仰角速度停止增大, 维持在最大值, 此时雷体已完全没入水中, 鱼雷处于带空泡航行阶段。直到0.35 s时, 俯仰角速度迅速减小, 俯仰角继续增大, 但是增大的趋势变小, 此时鱼雷侵水空腔逐渐闭合。

3.3 入水冲击加速度

鱼雷入水冲击后, 加速度无量纲的仿真曲线(cal)与试验曲线(exp)最大值和变化趋势比较一致, 如图7所示。鱼雷入水冲击后, 由于受到水的阻力作用,方向加速度在负方向迅速增大, 约0.02 s时达到最大值, 由图4可知, 此时雷头刚触水。随后方向加速度值逐渐减小。方向加速度在鱼雷触水后, 很短的时间内有一明显的正向增大趋势, 约5 ms时增大到最大值, 随后受到空泡所产生的低压力的影响, 迅速减小, 并出现负值, 约0.02 s时达到负向最大值, 然后加速度值缓慢减小。从向加速度变化鱼雷在斜入水过程中受力状态是比较复杂的, 既包括冲击力、阻力和力矩的作用, 还包括负向低压力的作用, 此力是由鱼雷头部空泡内的低压力产生, 会造成忽扑现象, 对鱼雷入水后的姿态有重要影响, 这也是鱼雷入水问题中常被忽略的作用力。

3.4 入水深度

鱼雷入水深度一直是工程上比较关心的问题, 关系到鱼雷实际的作战使用深度, 尤其是从鱼雷触水到全沾湿的深度, 影响鱼雷的起控时间。图8为鱼雷入水深度的仿真曲线和试验曲线, 深度随着时间几乎成线性增大。结合图4入水过程可知, 鱼雷全沾湿大约在0.4 s, 此时鱼雷入水深度约为3 m, 在此之前曲线吻合度较好, 之后全沾湿鱼雷尾舵影响较大, 曲线略有差异。

4 结束语

采用FEM/SPH耦合方法, 对鱼雷入水过程进行了仿真研究, 仿真结果与试验数据吻合较好, 验证了此方法对鱼雷入水问题研究的可靠性。

仿真分析了鱼雷入水后的运动姿态变化。鱼雷入水后, 受到“低头”力矩的作用, 俯仰角和俯仰角速度逐渐增大。由加速度可知, 鱼雷入水后受到冲击力作用, 加速度正向增大, 但是5 ms后, 由于雷头下部空泡所产生的负向低压力的作用, 加速度迅速减小并负向增大, 对鱼雷运动姿态影响较大。鱼雷全沾湿后的入水深度约为3 m。低压力是后续研究鱼雷入水姿态的关键。仿真结果可以为鱼雷入水弹道设计和结构承载能力设计提供分析依据。

[1] 徐宣志. 鱼雷力学[M]. 北京: 国防工业出版社, 1992.

[2] Von K T. The impact of seaplane floats during landing[R]. Washington USA: National Advisory Committee for Aeronautics, NACA TN 321, 1929: 1-8.

[3] Wagner V H. Phenomena associated with impacts and sliding on liquid surfaces[J]. Z Angew Math Mech, 1932(12):193-215.

[4] Oger G, Doring M, Alessandrini B. Two-dimensional SPH Simulations of Wedge Water Entries[J]. Journal of Computational Physics, 2005(213): 803-822.

[5] El-Mahdi Yettou, Alain Desrochers, Yvan Champoux. Experimental Study on the Water Impact of a Symmetrical Wedge[J]. Fluid Dynamics Research, 2006, 38(2): 47-66.

[6] Panciroli R. Water Entry of Flexible Wedges: Some Issues on the FSI Phenomena[J]. Applied Ocean Research, 2012, 39(3): 72-74.

[7] 严忠汉. 鱼雷入水初期水弹道稳定技术分析[J]. 水动力学研究与进展, 1990, 5(3): 117-126.Yan Zhong-han. The Technology of Stabilization of Initial Trajectory of Water Entry Torpedoes[J]. Journal of Hydrodynamics, 1990, 5(3): 117-126.

[8] 颜开, 史淦君, 薛晓中, 等. 用Mackey方法计算鱼雷带空泡航行时的入水弹道[J]. 弹道学报, 1998, 10(2): 93-96.Yan Kai, Shi Gan-jun, Xue Xiao-zhong, et al. The Water Entry Trajectory Calculation of a Torpedo With Cavity by Use of Mackey Method[J]. Journal of Ballistics, 1998, 10(2): 93-96.

[9] 潘光, 吴文辉, 毛昭勇, 等. 高空远程滑翔鱼雷全弹道仿真关键技术[J]. 鱼雷技术. 2009, 17(4): 10-15.Pan Guang, Wu Wen-hui, Mao Shao-yong, et al. Key Technologies about Complete Trajectory Simulation for High Altitude Long Range Gliding Torpedo[J]. Torpedo Technology, 2009, 17(4): 10-15.

[10] 安伟光, 蒋运华, 安海. 运动体高速入水非定常过程研究[J]. 工程力学, 2011, 28(3): 251-256.An Wei-guang, Jiang Yun-hua, An Hai. The Unstesdy Water Entry Process Study of High Speed Vehicle[J]. Engineering Mechanics, 2011, 28(3): 251-256.

[11] 邬明. 考虑空泡的空投航行器入水弹道研究[J]. 四川兵工学报, 2015, 36(3): 23-27.Wu Ming. Research on Water Entry and Underwater Trajectory of an Airborne Vehicle with Consideration of Cavity[J]. Journal of Sichuan Ordnance, 2015, 36(3): 23-27.

[12] 朱珠, 袁绪龙, 刘维. 柱体大攻角入水弹道建模与仿真[J]. 火力与指挥控制. 2015, 40(2): 13-23.Zhu Zhu, Yuan Xu-long, Liu Wei. On Modeling and Simulation of Cylinder Dropping in Water with High Angle of Attack[J]. Fire Control&Command Control, 2015, 40(2): 13-23.

[13] 郑兴, 段文洋. 光滑指点流体动力学(SPH)及算法特性[J]. 船舶力学, 2008, 12(4): 550-559. Zheng Xing, Duan Wen-yang. Smoothed Particle Hydrodynamics (SPH) and Its Numerical Behavior[J]. Journal of Ship Mechanics, 2008, 12(4): 550-559.

[14] 韩旭. 光滑粒子流体动力学——一种无网格粒子法[M]. 长沙: 湖南大学出版社, 2005.

(责任编辑: 许 妍)

Application of a FEM/SPH Coupling Method to Torpedo Water Entry

ZHANG Yue-qingCAI Wei-junLI Jian-chenWANG Zhi-jie

(The 705 Research Institute, China Shipbuilding Industry Corporation, Xi′an 710077, China)

To expand the application of a torpedo in shallow area of the sea, shallow water control technology is very important, and the unsteady motion parameters of the torpedo water entry are the input condition of initial control. In this paper, a simulation model of torpedo water entry is established by the FEM(finite element method)/SPH(smoothed particle hydrodynamics) coupling method, and the process of the torpedo from contacting with water to whole body wetting is simulated. The simulation results are in good agreement with the sea trial data, which indicates that the FEM/SPH coupling method has obvious advantage for solving torpedo water entry problem. Furthermore, the changing rule of movement attitude of torpedo water entry and the acceleration are analyzed by numerical simulation. The proposed method may become a reference for the study of torpedo water entry problem.

torpedo water entry; FEM/SPH coupling method; unsteady parameter

10.11993/j.issn.1673-1948.2017.01.001

TJ630.1; TB71.2

A

1673-1948(2017)01-0001-06

2016-11-19;

2016-12-18.

陕西省博士后科研项目资助.

张岳青(1984-), 男, 博士, 高级工程师, 主要研究方向为流固耦合研究.