基于遗传算法的鱼雷控制系统拓扑优化
2017-03-11张百勇
林 洋, 孙 炯, 刘 凯, 张百勇
基于遗传算法的鱼雷控制系统拓扑优化
林 洋1, 孙 炯2, 刘 凯2, 张百勇1
(1. 海军工程大学兵器系, 湖北武汉, 430033; 2. 海军工程大学科研部, 湖北武汉, 430033)
鱼雷控制系统对全雷正常运转起着至关重要的作用。针对其通信网络架构问题, 建立以某型鱼雷为实例的模型, 选取总线长度及可靠性优化为目标问题开展研究, 改进了遗传算法的求解效率及搜索全局最优解能力, 并利用MATLAB编程实现了对目标问题的求解。结果表明, 优化方案的拓扑结构在长度及可靠性上较该型雷的原设计结构更优。
鱼雷; 控制系统; 拓扑结构; 遗传算法
0 引言
鱼雷控制系统是控制全雷正常运作的关键, 而控制系统的显著特点便是其拓扑结构[1]。星型结构便于集中控制, 易于维护、安全, 但对中心节点可靠性有较高要求, 目前国产鱼雷的控制系统普遍采用的是这种架构。环网结构控制软件简单, 但网络响应时间长, 不便于扩充。总线结构费用低, 虽易于扩展但访问机制较复杂[2]。实际应用中, 控制系统的拓扑结构设计应考虑多个影响因素带来的约束条件, 整个系统中子系统或节点的重要程度不同, 可靠性要求存在差异, 其可靠性不仅取决于自身的可靠度及运行环境, 还与该节点的连线冗余程度有关, 同时, 节点的通信量要求也不相同, 另外还要考虑鱼雷内部复杂空间结构带来的区域限制等条件, 电磁兼容性问题等[3]。在其他领域, 针对系统的拓扑结构设计问题已有较多的研究案例, 在航空发动机领域, Thompson. H. A等人[4]利用多目标遗传算法对星型、环型、垂直、水平总线等4种结构进行了评估对比, 南京航空航天大学叶志峰团队[5]采用多目标遗传算法对发动机控制系统进行了结构优化的研究, 证明了多目标遗传算法对发动机控制系统的拓扑优化是可行的。在鱼雷控制系统的优化设计上, 目前针对拓扑结构的研究相对较少, 主要研究方向集中在节点模块化研究和通信总线类型的研究上[6], 对拓扑结构的设计缺乏系统地研究, 而智能算法得到的解是通过评价筛选得到的优势解, 利用智能算法实现拓扑结构优化设计的方法具有参考价值。文中在传统遗传算法的基础上, 改进算法计算周期及其求最优解效率, 以系统连线及节点冗余可靠性为优化目标对各类拓扑类型进行最优结构求解, 最后综合各类最优解特点计算综合最优的拓扑结构。
1 问题陈述
1.1 控制系统通信网络模型
图1为某型雷控制系统模型, 各子系统或节点标号~。以连线长及节点冗余度为优化目标, 不考虑其他约束条件, 为简化运算过程, 假设如下:
1) 忽略不可布线区域, 节点连线长度采用空间距离计算;
2) 各节点均分布在包含鱼雷纵向中轴线的平面内, 其余位置特性参考该型鱼雷设计手册。
1.2 问题定义
由于设各节点分布于同一平面, 且优化目标为总线长及节点冗余可靠性, 不涉及节点之间的方向问题, 可用无向图的优化等价该目标[7]。

(2)
(3)
各节点的连接关系用图的邻接矩阵表示, 定义邻接矩阵

其中
(5)
由于考虑节点冗余度及总线长, 目标问题函数可归一为


为使所求解符合实际情况, 加入以下筛选条件。
1) 任意节点不能被孤立
所得解中不能出现孤立节点, 即每一节点的冗余度至少为1。
2) 无向图必须连通
图论中, 连通性表示任意2个节点之间存在有效的连接路径, 求解过程中, 会出现若干独立连通区域的解的情况, 根据图论理论, 图的连通性与图的邻接矩阵有关[8]

在优化过程中, 验证式(8)中幂次和矩阵任意行和不为零即可筛除此类解,为节点数目。
3) 重要节点的冗余度设置
文章的目的在于优化求解最优总线长及节点冗余可靠性, 为此, 参考设计手册, 对部分节点增加冗余度约束。
2 算法设计及优化结果
遗传算法是模拟达尔文生物进化论中遗传学机理和自然选择的计算方法, 通过一个随机生成的初始种群开始反复迭代进化, 进化过程中的算子模仿生物界的进化机制, 包括选择、交叉、变异等操作不断提高种群的适应度, 适应度的计算方法与所求问题的目标函数相关, 直到算法收敛或迭代停止, 此时, 所得种群中最优适应度个体即为所求目标问题最优解[9]。
2.1 个体编码
由式(6)和式(7)可知, 求解过程变量为邻接矩阵, 观察可知其为主对角线为0的对称矩阵, 且任意元素为0或1, 采用二进制向量的编码方式, 将邻接矩阵的上三角部分逐行依次组合构成一个多维二进制行向量, 如图2所示。
2.2 适应度函数
适应度函数用以评价个体的优劣程度, 决定个体在进化过程中遗传至下一代的概率, 文中需要求解式(6)的最小解, 对目标函数作如下变换, 得适应度函数
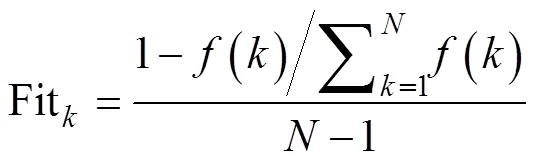
2.3 遗传算子及算法改进
简单遗传算法中, 主要使用选择、变异和交叉3个算子模拟生物的进化过程, 传统遗传算法搜索效率低, 对大解空间问题容易陷入局部最优解而收敛, 为此提出以下改进措施。
1) 动态算子
传统算法中, 交叉和变异概率往往根据经验选择且固定不变, 难以保证当种群规模大幅扩增时的搜索效率或种群数急剧下降的过早收敛, 主要原因在于遗传算法自身是一个动态搜索过程, 种群进化过程中, 多样性及规模在不断变化[10], 为保证算法高效, 需根据以上因素设定相应的动态交叉和变异概率。

(11)
2) 精英保留策略
传统遗传算法中, 参与进化个体会被直接破坏, 导致优秀个体概率性被淘汰, 而Rudolph已经采用有限马尔可夫链理论证明了仅采用交叉、变异和选择3个遗传算子不能收敛到全局最优值, 为此De Jong[11]定义了一种精英保留策略, 参与运算个体若在下一代中不存在, 则加入到下一代种群中, 否则剔除, 并证明了具有精英保留策略的遗传算法是全局收敛的。
3) 并行群间竞争
为了提高运算效率, 一个体首3位编码为标识编码, 建立8个种群并行求解, 迭代过程中, 种群之间独立, 每迭代若干代后群间随机配对进行选择淘汰, 重复这一过程直到算法收敛[12]。
2.4 算法仿真及运算结果
设定算法参数如表1所示。

表1 算法参数
表1中:1为初代种群数;2为初代种群规模;为进化代数;为群间竞争间隔代数。
通过MATLAB软件编程实现算法, 设定表1参数, 得出结果如图3所示。
各拓扑类型求得最优个体参数见表2。
观察表2结果可知, 树型结构在总线长上最小, 总线型结构较树型结构节点冗余度更高, 而环网结构的节点冗余度最优, 综合考虑总线长及节点冗余度两者, 以总线型结构为基础, 计算时对系统中重要节点冗余度设置大于2的约束条件, 计算所得结果如表3所示。
该个体实际连线如图4所示。
以冗余度数为权值衡量各结构冗余度可靠性, 所有试验结果对比排序为冗余度可靠性:;总线长:。

表2 优化结果
表2中:为拓扑类型;1为原设计结构;2为树型结构;3为环网结构;4为总线结构;为冗余度为的节点数;为拓扑总线长。

表3 混合结构优化结果
表3中,5表示混合结构。
结合图4可知, 该试验得出的混合型拓扑结构是综合最优的, 即环网和总线型结构综合的拓扑方式在最小化总线长及最大化节点冗余度方面综合最优, 较该型雷原设计更优。
2.5 试验结果有效性验证
为了验证试验结果的有效性, 选择一个多峰值函数验证改进算法, 与传统遗传算法进行实例仿真对比

图5 实例函数图像
Fig. 5 Graph of example function
从图5可以看出, 在该区间上, 该实例函数有较多个峰值, 分别利用改进的遗传算法和传统遗传算法, 设定1 000初始种群规模数, 对其进行该区间上最大值搜索, 迭代结果如图6所示。
观察可知, 传统遗传算法迭代了54次得到收敛解, 而改进算法迭代了39次就得到了收敛解, 且最优解与实际解值如表4所示。
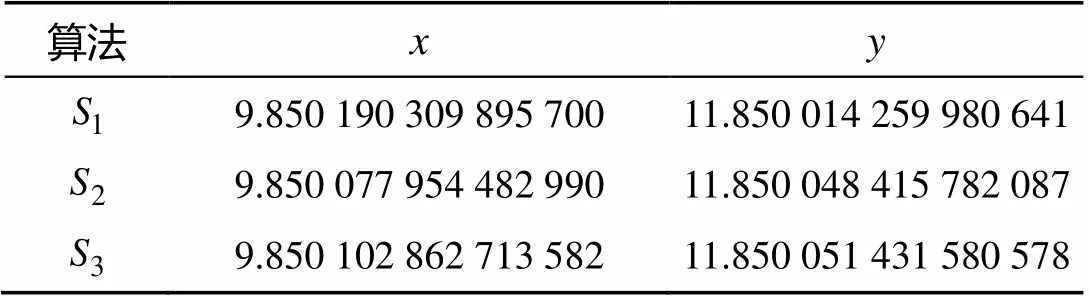
表4 算法迭代结果
表4中:1为传统遗传算法;2为改进算法;3为求导实际解。
由上述结果可知, 改进方法较传统遗传算法, 在提高算法收敛速率的同时, 所得的解也能够更准确搜索到实际该函数的最大值, 证明该改进方案在搜索效率及保证最优解上较传统遗传更加可靠, 由此, 试验所得优化的鱼雷控制系统拓扑结构是可行并具有参考价值的。
3 结束语
文中在建立简化模型的基础上, 以系统总线长及节点冗余可靠性为优化目标, 改进了遗传算法的求解周期及最优解搜索效率, 将拓扑结构优化问题等价为带约束的平面无向图优化问题并进行求解计算, 得出了综合优化的结构, 结果证明优化方案较该型雷原设计结构在总线长及节点冗余度可靠性上更优。实际上, 文中考虑的约束条件较少, 在计算过程中, 为简化运算, 忽略了雷内空间结构的硬性约束。在实际的优化设计过程中, 单一以总线长及节点冗余可靠性为优化目标是不全面的, 需要考虑的有包括通信协议确定的节点主从关系、雷内实际空间限制要求、节点之间通信量需求, 电磁兼容等等诸多约束条件, 下一步工作将结合实际情况考虑多目标的综合优化问题。
[1] 黄樟灿, 杨鹏, 李亮, 等. 网络拓扑结构的数学模型及遗传算法[J]. 计算机工程与应用, 2001, 37(2): 68-69.
[2] 魏柏舟. 网络拓扑结构类型简论[J]. 才智, 2012(25): 54.
[3] 汤丽丽, 宋军强, 潘慕绚, 等. 航空发动机分布式控制通讯网络拓扑结构优化[J]. 航空发动机, 2015, 41(2): 27-30.Tang Li-li, Song Jun-qiang, Pan Mu-xuan, et al. Optimization of Topology Structure for Aeroengine Distributed Control System Communication Network[J]. Aeroengine, 2015, 41(2): 27-30.
[4] Thompson H A, Fleming P J. A Transputer-based Fault- tolerant Architecture for Gas Turbine Engine Controllers[C]//IEEE Colloquium on Fault Tolerant Techniques. [s.l.]: IEEE, 1990: 8/1-8/5.
[5] 张世维. 航空发动机分布式控制系统结构多目标优化[D]. 南京: 南京航空航天大学, 2007.
[6] 魏玉华, 朱云周, 高卓. 一种基于复合拓扑结构的鱼雷高速光纤总线设计[J]. 鱼雷技术, 2016, 24(2): 117-118.Wei Yu-hua, Zhu Yun-zhou, Gao Zhuo. A High-speed Optical Fiber Communication Bus in Torpedo Based on Complex Topological Structure[J]. Torpedo Technology, 2016, 24(2): 117-118.
[7] 关越. 航空发动机分布式控制系统通信总线研究[D]. 南京: 南京航空航天大学, 2013.
[8] 龙亚. 图的连通性算法探讨[J]. 毕节师范高等专科学校学报(综合版), 2002, 20(1): 70-71. Long Ya. An Approach to the Algorithm of the Graphic Cinnectivity[J]. Journal of Bijie Teachers College, 2002, 20(1): 70-71.
[9] 王煦法. 遗传算法及其应用[J]. 小型微型计算机系统, 1995(2): 59-64.
[10] 张宇, 郭晶, 周激流. 动态变异遗传算法[J]. 电子科技大学学报, 2002, 31(3): 234-239. Zhang Yu, Guo Jing, Zhou Ji-liu. Dynamic Mutation Genetic Algorithm[J]. Journal of University of Electronic Science and Technology of China, 2002, 31(3): 234-239.
[11] Jong K A D. An Analysis of the Behavior of a Class of Genetic Adaptive Systems[D]. USA: University of Michigan Ann Arbor, 2010.
[12] 郭凯. 遗传算法的3种改进方法和分析[J]. 电子测试, 2011(3): 38-40. Guo Kai. Three Kinds of Improved Genetic Algorithm and Analysis[J]. Electronic Test, 2011(3): 38-40.
(责任编辑: 许 妍)
Optimization of Topology Structure for Torpedo Control System Based on Genetic Algorithm
LIN Yang,SUN Jiong, LIU Kai,ZHANG Bai-yong
(1. Department of Weapons, Naval University of Engineering, Wuhan 430033, China; 2. Office of Research and Development, Naval University of Engineering, Wuhan 430033, China)
Aiming at the optimization of communication network architecture of torpedo control system, a simple model is established for a certain type of torpedo. The total length of the lines for connection in the control system and the reliability of network are chosen as the optimizing target, the solving efficiency of genetic algorithm and the ability of searching global optimal solution are improved, and the solution to the target optimization problem is achieved by programming with MATLAB. The result shows that the optimized topology structure is better than the original one in the total length of connection lines and the network reliability.
torpedo; control system; topology structure; genetic algorithm
10.11993/j.issn.1673-1948.2017.01.006
TJ630.33; TP18
A
1673-1948(2017)01-0027-05
2016-07-20;
2016-08-26.
林 洋(1991-), 男, 在读硕士, 主要研究方向为武器系统运用与保障工程.
