准确把握函数的对称性解题例说
2017-03-10
准确把握函数的对称性解题例说
☉浙江省宁海县知恩中学 徐明月
对称性是函数的重要性质,其中主要有两种类型:
(1)一个函数自身的对称性.
对于特殊的函数,如奇函数关于原点对称,偶函数关系y轴对称.对于函数f(x),若存在常数a使得任意x,都有f(a+x)=f(a-x),则f(x)关于直线x=a对称;对于函数f(x);若存在常数a,b,使得任意x,都有f(2a-x)=2b-f(x),则函数f(x)关于点(a,b)成中心对称等等.
(2)两个函数之间的对称性.
底数相同的指数函数与对数函数互为反函数,两个函数的图像关于直线y=x对称;y=f(x)与y=f(-x)关于y轴对称;y=f(x)与y=-f(x)关于x轴对称;y=f(x)与y=-f(-x)关于原点对称,y=f(x)与y=-f(2a-x)+2b关于点(a,b)对称等等.
解题中要准确识别对称的类型,利用相关的对称性解题.
一、关于直线y=x对称
若两个函数互为反函数,则这两个函数的图像关于直线y=x对称,常见的类型是底数相同的指数函数与对数函数互为反函数.
例1已知函数y=ax,y=xb,y=logcx的图像如图1所示,则().
A.a>b>c
B.a>c>b
C.c>a>b
D.c>b>a
解析:a为指数函数的底数,b为幂函数的指数,c为对数函数的底数.

图1
对于a,c,由指数函数与对数函数的图像,易知a>1,c>1,但不易直接比较大小.利用指数函数与对数函数互为反函数的关系,将y=ax的图像转化为其反函数y=logax的图像,如图1中粗线所示.进而可得出c>a.
故正确选项为C.

由图像关于y=x对称得|PQ|最小值为2dmin=(1-ln2).
故正确选项为D.
二、关于y轴对称
若函数y=f(x)为偶函数,则对于任意的x,都有f(-x)=f(x)=f(|x|),解题中利用此关系,常可有效避免分类讨论.
例2(2015年天津理科卷)已知定义在R上的函数f(x)=2|x-m|-1(m为实数)为偶函数,记a=f(log0.53),b=f(log25),c=f(2m),则a,b,c的大小关系为().
A.a<b<cB.a<c<bC.c<a<bD.c<b<a
解析:因为函数f(x)=2|x-m|-1为偶函数,所以m=0,即1=2,
b=f(log25)=2log25-1=4,c=f(2m)=f(0)=20-1=0.
所以c<a<b.
故正确选项为C.
变式已知函数f(x)=x2+ex-(x<0)与g(x)=x2+ ln(x+a)的图像在存在关于y轴对称点,则a的取值范围是().

解析:由题条件易知,存在x0∈(-∞,0),满足+ex0 -=(-x)02+ln(-x0+a)⇒ex0 -ln(-x0+a)-=0有负根,当x趋近于负无穷时,ex0 -ln(-x0+a)-趋近于负无穷,因为函数h(x)=ex-ln(-x+a)-在定义域内是单调递增,所以h(0)=-lna>0,所以lna<ln⇒a<,故选B.
三、关于原点对称
若函数y=f(x)为奇函数,则对于任意x,都有f(-x)= -f(x),或f(-x)+f(x)=0.根据条件准确识别出相关的性质是问题顺利求解的关键.
例3已知函数f(x)的定义域为R,∀a,b∈R,若此函数同时满足:①当a+b=0时,有f(a)+f(b)=0,②当a+b>0时,有f(a)+f(b)>0,则称函数f(x)为Ω函数.
下列函数:①y=x+sinx;②y=3x-()x;③y=是Ω函数.(填出所有符合要求的函数序号)
解析:由条件①知,当a=-b时,f(-b)+f(b)=0,进而可知函数f(x)为奇函数;
由条件②知,当a>-b时,有f(a)>-f(b)=f(-b),即函数f(x)在定域内为增函数.
函数y=x+sinx与函数y=3x-()x既是增函数;函数为奇函数,但不是非单调函数.
故正确答案为①②.
变式平面若直角坐标系内的两点P、Q满足条件:①P、Q都在函数y=f(x)的图像上,②P、Q关于原点对称,则称点对[P,Q]是函数y=f(x)的一对“友好点对”(注:点对[P,Q]与[Q,P]视为同一对“友好点对”).
A.0B.1
C.2D.3
解析:此题的关键点在于y轴两侧的点关于原点对称,故可联想到函数的奇偶性,即奇函数的性质,作出f(x)=-x2-4x(x<0),关于原点对称的图像,如图2中虚线所示,即可得出其与函数f(x)=log2x(x>0)的交点个数为2,故答案C.
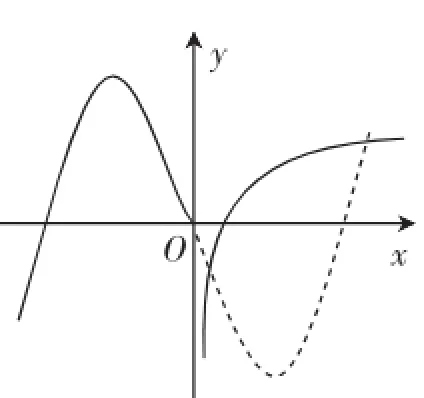
图2
四、关于直线x=a对称
例4(2015年福建卷)若函数f(x)=2|x-a|(a∈R)满足f(1+x)=f(1-x),且f(x)在[m,+∞)单调递增,则实数m的最小值等于_______.
解析:由f(1+x)=f(1-x)得函数f(x)关于x=1对称,故a=1,则f(x)=2|x-1|,由复合函数单调性得f(x)在[1,+∞)递增,故m≥1,所以实数m的最小值等于1.
变式已知函数f(x)=cosxsin2x,判断函数f(x)的图像是否关于直线x=对称.
五、关于点(a,b)对称
例5(2016年全国卷Ⅱ)已知函数(fx)(x∈R)满足(f-x)=2-(fx),若函数y=与y=(fx)图像的交点为(x,
1y)1,(x2,y)2,…,(xm,ym),则(xi+y)i=().
A.0B.mC.2mD.4m
解析:由f(-x)=2-f(x),得f(x)关于(0,1)对称,而y=也关于(0,1)对称,所以对于每一组对称点xi+xi′=0,yi+yi′=2,所以m,故选B.
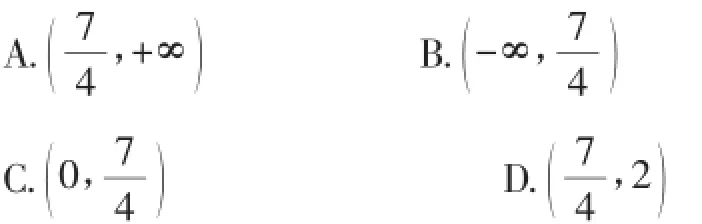

图3
总之,在解答与函数对称性相关的问题中,要准确识别出函数的性质,图像关于直线对称,还是关于点对称,是一个函数自身的对称性,还是两个函数间的对称性,从而准确利用其解题.
