数学概念、性质教学的一点建议
——以苏教版椭圆性质教学为例
2017-03-10
数学概念、性质教学的一点建议
——以苏教版椭圆性质教学为例
☉江苏省海安县曲塘中学 周爱琴
在高中数学某些性质、定理的教学中,部分教师采用让学生先记忆,再进行解题应用训练来达到熟练程度的办法,对相关性质、定理的得出并未进行推理、说明,学生往往也是只知道有这个性质,但这个性质是如何得出的,并不清楚.因此在创新问题的解答中往往找不到问题的切入点.
一、引例说明
题目曲线C是平面内与定点F(2,0)和定直线x=-2的距离的积等于4的点的轨迹.下列四个结论:
①曲线C过坐标原点;②曲线C关于x轴对称;③曲线C与y轴有3个交点;④若点M在曲线C上,则|MF|的最小值为2(-1).
其中,所有正确结论的序号是___________.
定义一个新曲线,考查曲线相应的几何性质.考查学生即时学习的能力,培养学生创新意识.从数(方程)与形(曲线)两个角度认识事物.解答此题的方法其实在教材中都能找原型,如苏教版教材“圆锥曲线与方程”椭圆的简单几何性质一节中均有详细的说明.
二、解法探源
以焦点在x上的椭圆方程为例.
1.椭圆上的点(x,y)的坐标范围
2.椭圆的对称性
3.椭圆的顶点
4.椭圆上的点到焦点的距离最值问题
所以当x=-a时,|PF1|min=a-c;当x=a时,|PF1|max=a+c.
其实上述性质通过直接观察椭圆的图形即可得出,也不难理解、容易接受.但是如果我们真的这样做了,那就失去了培养学生解题能力的一次有利时机.
三、问题解答
曲线C是平面内与定点F(2,0)和定直线x=-2的距离的积等于4的点的轨迹:设M(x,y)是曲线C上任意一点,则有此方程若进一步化简较为复杂,但这并不影响我们对题目所给结论正确性的判断:
对于结论①,判断曲线C是否过坐标原点,可将x=0, y=0代入方程中,等式成立,故结论①正确.
说明:此结论的判断方法源于椭圆顶点的求解.
对于结论②,判断曲线C是否关于x轴对称,可令-y代换方程中的y,方程不改变,所以曲线C关于x轴对称,故结论②正确.
说明:此结论的判断方法源于椭圆对称性的判断.
说明:此结论的判断方法源于椭圆顶点的求解.
故结论④正确.
说明:此结论的判断方法源于椭圆上点的坐标范围的确定及椭圆上的点到焦点距离的最值问题的求解.
综上所述,本题的正确答案为①②④.
四、变式拓展
变式曲线C是平面内与三个定点F(1-1,0),F(21,0)和F(30,1)的距离的和等于2的点的轨迹.给出下列四个结论:①曲线C关于x轴、y轴均对称;②曲线C上存在一点P,使得③若点P在曲线C上,则△F1PF2的面积最大值是1;④三角形PF2F3面积的最大值
其中所有真命题的序号是_________.
解析设曲线C上任意一点为P(x,y).由题意可知,C的方程为
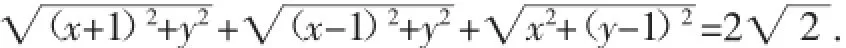
对于结论①,在此方程中,用-x,-y分别取代x,y,可知C只关于y轴对称,不关于x轴对称.故结论①错误.
对于结论③,因为|PF1|+|PF2|≤|PF1|+|PF2|+|PF3|=2,所有的P点都应该在椭圆D:+y2=1内(含边界),曲线C与D有唯一公共点A(0,1),此时,三角形面积最大,最大值为1.故结论③正确.
对于结论④,△PF2F3面积的最大值为此时需要先考虑以F2,F3为焦点、实半轴为的椭圆E,其短轴顶点到直线F2F(3x+y-1=0)距离为,此时△PFF的23面积为,但是曲线C应该在此椭圆内部,所以三角形PF2F3的面积应小于.故结论④错误.
综上所述,本题正确答案为③.
五、教学反思
通过上述两例的分析,我们不难发现,对于一道所谓的难题,“难”往往只是体现在问题的形式,透过表象,不难发现问题的求解方法其实都是我们熟悉的内容,关键在于有没有引起我们足够的重视.
教材是历代教学专家智慧的结晶,是高考命题的主要依据,很多教师在教学中对教材内容的重视不够,常常是少讲甚至不讲,脱离教材.例如很多学生在学完了双曲线的有关内容之后,仍然不知道为什么双曲线的离心率越大,曲线的开口越大.是教师不知道吗?当然不是,只是他们对这一原理没有进一步解释,其实道理很简单,因为离心率,所以离心率越大,越大,曲线的开口越大.
教材中的每一个知识点,甚至每一道例题或习题都是众多专家精心编排的,具有典型性、代表性、发散性,很多高考命题都是在这些内容的基础上衍变而来,即使是综合题的命制也例外,也是由教材中例题或习题的组合、深度加工和拓展而来,因此对教材内容不能孤立地看待,要抓住重点,并且善于从各个方面精心挖掘其内存的潜能,使教材中的每一个知识点、每一道例习题都能充分发挥其应有的作用.
操作起来其实很简单,在讲解某一知识点时,只要我们讲清楚该知识点的来龙去脉,并对教材内容进行有效的追问、拓展,将问题的背景进行引伸,将问题形式进行变换,这样就能有效激活学生的思维,帮助学生建立章节内部及章节之间的知识网络,形成系统,进而有效促进学生分析问题能力、解决问题能力的提高与发展.
