赏析几例圆锥曲线切线问题

2017-03-10

中学数学杂志 2017年3期

关键词：补角对称点切点

赏析几例圆锥曲线切线问题

☉江苏省南通市通州区教学研究室王惠清

圆锥曲线是一组非常优美和谐的曲线，笔者在平时的教学实践中发现了其中的一些优美性质，下面举几例，以飨读者.

一、圆锥曲线切线中的一个定值问题

设PA，PB分别是焦点为F的抛物线的两条切线，A，B为切点，过抛物线上任意一点C作切线分别交直线PA，PB于M，N两点，当点C移动时，∠MFN大小不变（如图1）.

通过探究，对于椭圆和双曲线也有同样的结论，具体的情形就是本文的定理1，2，3.下面给出几何法的证明.

图1

图2

引理1设PA，PB分别是焦点为F的抛物线的两条切线，A，B为切点，则有∠PFA=∠PFB.

证明：如图2，设l为抛物线的准线，分别过点A，B作l的垂线，垂足D，E.由抛物线的定义及光学性质知，AF= AD，D，F两点关于切线PA对称（从点F射出的光线经抛物线上的点A反射后将垂直于准线射出，相当于从准线上的点D直接射出），此时的切线PA相当于在点A处的一面平面镜，所以△PFA与△PDA全等，PD=PF.同理，PE= PF，从而PD=PE，∠1=∠2，∠PDA=∠PEB，即∠PFA=∠PFB得证.

引理2设PA，PB分别是焦点为F的抛物线的两条切线，A，B为切点，则有∠PFA+∠APB=π.

证明：如图2，夹在两平行线DA，EB之间的∠PDA+∠PEB+∠3+∠4+∠5+∠6=2π，因为∠PDA=∠PEB，∠3=∠4，∠5=∠6，所以∠PDA+∠4+∠5=π，即∠PFA+∠APB=π，得证.

此外，还有△PAF与△BFP相似；PF2=AF·BF；∠AFB=2∠APB等结论，留给读者证明.

定理1设PA，PB分别是焦点为F的抛物线的两条切线，A，B为切点，过抛物线上任意一点C作切线分别交直线PA，PB于M，N两点，当点C移动时，∠MFN大小不变，且∠MFN+∠APB=π，即点P，N，F，M四点共圆.

证明如图3，由于MA，MC是两条切线，根据引理1知，∠AFM=∠CFM.同理NB，NC是两条切线，根据引理1知，∠BFN=∠CFN，所以∠CFM+∠CFN=（∠PFA+∠PFB）=∠PFA，即∠MFN=∠PFA，即∠MFN大小不变得证；再由引理2，∠MFN+∠PFA=π，所以点P，N，F，M四点共圆.

引理3设PA，PB分别是焦点为F1，F2的椭圆的两条切线，A，B为切点，则有∠PF1A=∠PF1B，∠PF2A=∠PF2B.

图3

图4

证明：如图4，作点F1关于切线PA的对称点D，△PAD与△PAF1全等，∠1=∠2.由椭圆的光学性质，从F1发出的光线经椭圆反射后经过另一焦点F2，相当于光线从点D直接经过A到达F2，由椭圆定义，DF2=AF1+AF2等于椭圆的长轴长.作点F1关于切线PB的对称点E，△PBE与△PBF1全等，∠3=∠4，由椭圆的光学性质，从F1发出的光线经椭圆反射后经过另一焦点F2，相当于光线从点E直接经过B到达F2.由椭圆定义，EF2=BF1+BF2等于椭圆的长轴长.因为PD=PE=PF1，DF2=EF2，故△PDF2与△PEF2全等，∠5=∠6，即∠PF2A=∠PF2B得证.同时得∠1=∠4，从而∠2=∠3，即∠PF1A=∠PF1B得证.

引理4设PA，PB分别是焦点为F1，F2的双曲线同一支的两条切线，A，B为切点，则有∠PF1A=∠PF1B，∠PF2A=∠PF2B.

证明：如图5，作点F2关于切线PA的对称点D，△PAD与△PAF2全等，∠5=∠7，由双曲线的光学性质，从F2发出的光线经双曲线反射后的反向延长线经过另一焦点F1，相当于光线从点F1经过D到达A，由双曲线定义，DF1= AF1-AF2等于双曲线的实轴长.同理得△PBE与△PBF2全等，∠6=∠8，EF1=BF1-BF2等于双曲线的实轴长.因为PD=PE=PF2，DF1=EF1，得△PDF1与△PEF1全等，∠1=∠2，即∠PF1A=∠PF1B得证.同时得∠3=∠4，从而∠5=∠6，∠7=∠8，即∠PF2A=∠PF2B得证.

图5

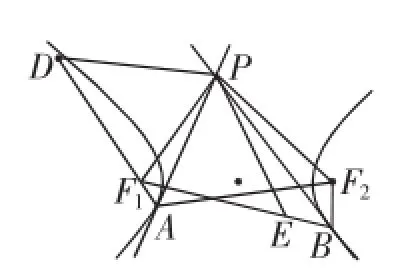
图6

引理5如图6，设PA，PB分别是焦点为F1，F2的双曲线的两条切线，当切点A，B不在同一支上时，则有PF1平分∠AF1B的外角，PF2平分∠AF2B的外角.

证明与引理4的证明类似，不再赘述.

定理2如图7，设PA，PB分别是焦点为F1，F2的椭圆的两条切线，A，B为切点，A′，B′分别是A，B关于中心O的对称点，若过椭圆上A′，B′之间的实线部分任意一点C作切线分别交直线PA，PB于M，N两点，∠MF1N与∠MF2N大小不变，且分别等于∠PF1A与∠PF2A；若过椭圆上A′，B′之间的虚线部分任意一点C作切线分别交直线PA，PB于M，N两点，∠MF1N与∠MF2N大小不变，且分别等于∠PF1A的补角与∠PF2A的补角.

图7

图8

定理3如图8，设PA，PB分别是焦点为F1，F2的双曲线的两条切线，A，B为同一支上切点，A′，B′分别是A，B关于中心O的对称点，若过双曲线上的实线部分（以A′，B′为界）任意一点C作切线分别交直线PA，PB于M，N两点，∠MF1N与∠MF2N大小不变，且分别等于∠PF1A与∠PF2A；若过双曲线上A′，B′之间的虚线部分任意一点C作切线分别交直线PA，PB于M，N两点，∠MF1N与∠MF2N大小不变，且分别等于∠PF1A的补角与∠PF2A的补角.

图9

如图9，设PA，PB分别是焦点为F1，F2的双曲线的两条切线，当切点A，B不在同一支上时，A′，B′分别是A，B关于中心O的对称点，若过双曲线上的实线部分（以A′，B′为界）任意一点C作切线分别交直线PA，PB于M，N两点，∠MF1N与∠MF2N大小不变，且分别等于∠PF1A与∠PF2A；若过双曲线上的虚线部分任意一点C作切线分别交直线PA，PB于M，N两点，∠MF1N与∠MF2N大小不变，且分别等于∠PF1A的补角与∠PF2A的补角.

定理2和定理3的证明过程与定理1的证明过程类似，只要利用引理3，4，5就行了.只是椭圆和双曲线有两个焦点，另外，切点C在实线上与在虚线上需要讨论，还有双曲线中PA，PB切在同一支上和切在两支上，情形更多，限于篇幅，不再赘述.