一道“伪坐标题”的命题商榷与变式改编

☉江苏江阴市第二中学 徐燕君

一道“伪坐标题”的命题商榷与变式改编

☉江苏江阴市第二中学 徐燕君

近年来，我们在《中学数学》（初中版）阅读了不少命题商榷类的文献，增长了见识，知道了中考题也不一定都是好题.比如，一类“伪坐标系”的考题在不少文献中多有批判，言之确凿，看似函数问题，其实与函数图像几无关系，当函数解析式求出之后，图像上一些点的位置确定之后，就演变成几何问题唱大戏.这类“伪坐标系”问题在不少地区的考题中仍然频繁上演.笔者近期就碰到一道中考模考卷的压轴题，也属这类“怪怪的考题”.以下先概述这道考题及求解思路，并跟进结构反思，最后给出命题商榷和命题改编，供研讨.

一、考题讲解与结构反思

图1

（1）求直线AB的解析式；

（2）设点P在直线AB上，△COP的周长最小时，求点P的坐标；

（3）若抛物线的对称轴与x轴交于点D，直线l经过点D且与AB平行，点E在线段AD上运动（不与A、D重合），点F在直线l上运动，且∠BEF=60°，比较线段BE与EF的大小，并证明你的结论.

（2）根据轴对称最小值模式（光线反射原理）可构造图2分析，取点C关于AB的对秒点C′，连接OC′，交AB于点P，则点P为所求.

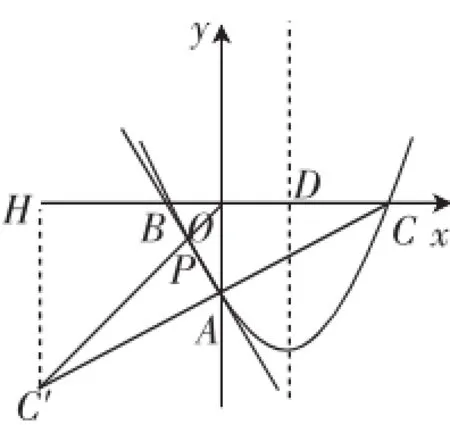
图2

接下来是如何求点P的坐标，比如，走“解析路径”是可以的，根据相似三角形（△COA∽△CHC′）可确定点C′的坐标，接着可解出直线OC′的解析式x.联立直线OC′和AB的解析式，即可得点P的坐标.

殊途同归：也可走几何相似法求出点P的坐标，比如，构造图3，可获得等边三角形CEC′的结构认识，直线AB恰经过等边三角形的顶点E.利用△OAP∽△C′EP，结合相似比可求出点P的横、纵坐标.

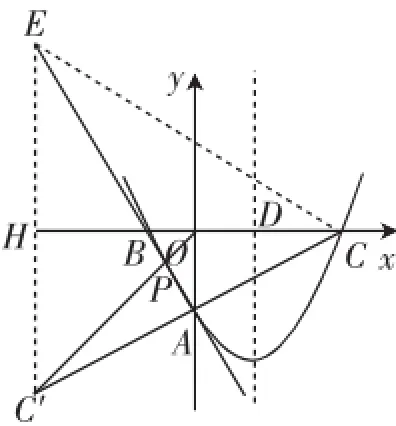
图3

（3）先构造图4分析，线条繁多，思路较难获得，我们可以确认几个信息：△ABD是等边三角形，∠BDF=60°.

现在把图形的无关线条删减成图5这样的结构：

在图5中，等边△ABD中，点E为AD边上一点，∠BEF=60°，边EF交△ABD的外角平分线于F.在AB边上取一点G，构造等边三角形AGE，从而只要证△BEG≌△EFD即可实现问题突破.

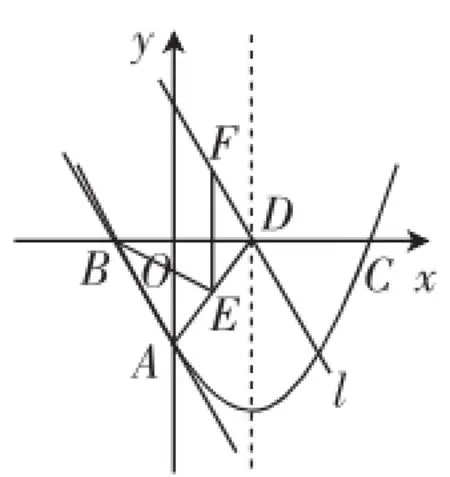
图4

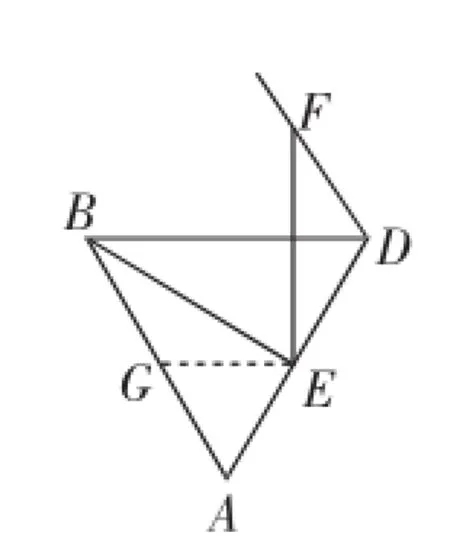
图5

解后反思：第（2）、（3）问分别对应着两个基本图形，即：光线反射原理；等边三角形为背景的一类全等问题.以下就是一类典型问题及其变式：

同类题链接：如图6，已知△ABC与△CDE都是等边三角形，点B、C、D在一条直线上，点P为直线BC上一动点，且∠APQ=60°，PQ交直线CE于点Q，连接AQ.

我们知道，当点P在边BC上、BC的延长线上时，都可证得△APQ是等边三角形.

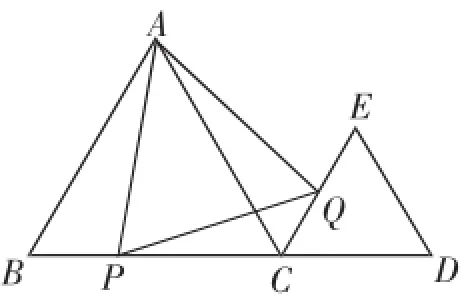
图6

图7

同类题拓展：如图7，点A、B、E在同一直线上，作正方形ABCD、正方形BEMN，点P为AB边上一点，连接PD，过点P作PQ⊥PD，交直线BM于点Q，一定有线段PD、PQ是相等的；如果连接DQ，则可证△PDQ是等腰直角三角形.

二、命题商榷与变式改编

1.伪坐标系问题从表面上看是综合考查，实则貌合神离.

网上一些所谓的以二次函数为载体的综合题，其中大量属于伪坐标系问题，就如上文中的考题一样，当抛物线明确之后，各个交点随之确定，进一步的设问探究与函数、函数图像都无关.这种题目看似以二次函数或图像为平台展开设问，实质上函数题干信息已提前枯萎，后面生长出去的问题已无关函数.

2.繁杂的几何构造不宜组合在综合题中.

一般来说，根据教学经验，学生在限时独立完成的考场上答题时最怕的是在代数几何综合题中遇到需要复杂构造的几何问题，有时单独把这种几何题分离出来，答题效果会好很多.就如上面提到的图6、图7的证明，但是将其融合在抛物线为背景的所谓的综合题中，能在较短时间内顺畅地获得思路的学生少之又少.

3.深刻理解函数概念，在函数本质处设问考查.

近年来，章建跃教授提出的“三个理解”（理解数学，理解学生，理解教学）“搔到痒处”，得到一线教师的广泛共鸣，一个显著标志是，在中国知网上以“三个理解”为关键词、主题词检索初中数学教学研究文章时，会出现大量的相关文章，特别是以案例跟进式研究文献居多.对于函数综合题来说，我们认为命题者应该基于深刻理解函数概念的基础，在函数本质处设问，比如，函数中的参数问题、函数的增减性、函数的最值、函数中的数形结合分析法等.知易行难，下面我们给出一道改编题，供研讨：

（1）当点D与点A关于抛物线的对称轴对称时，求S的值；

（2）当点D位于什么位置时，S取得最大值？求出D点的坐标与S的最大值；

（3）若点M是直线AB上一个动点，当△COM的周长最小时，求M点的坐标.

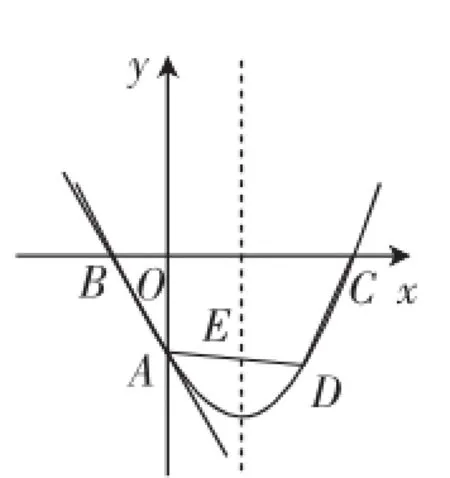
图8

三、写在后面

命题研究是教学研究中的一个基本问题，命题时首先要确立正确的命题“价值观”，如果认为各级考卷中的题都是权威的、正确的，网上、教辅上流行的都是好的题目，那么自己的命题往往会走偏方向.通过精研数学，理解数学，深入理解教材上的概念、例题和习题设计的意图，知道“好的题目”（章建跃语）追求简洁、易懂、深刻、与上下左右充满关联，等等，则自己的命题成果很有可能会引领学生理解数学、感悟本质，善莫大焉.

1.章建跃.“题型+技巧”的危害［J］.中小学数学（高中版），2010（11）.

2.付小飞.明辨并列与递进，引导分离和聚焦——2016年江苏苏州中考第28题解析与教学思考［J］.中学数学（下），2016（7）.

3.宋秀云.让“简单内容”教得深刻［J］.数学通报，2016，55（4）.

4.向中军.试题命题应紧扣教材和课标［J］.中学数学教学参考（中），2016（5）.