动点函数
——中考的“常青藤”
2017-03-10江苏如东县掘港镇童店初级中学沈卫卫
☉江苏如东县掘港镇童店初级中学 沈卫卫
动点函数
——中考的“常青藤”
☉江苏如东县掘港镇童店初级中学 沈卫卫
纵观每一年的中考题,不难发现有一类动点函数的选择题屡屡出现,成为中考场上的亮点.这类题一般处在选择压轴题的位置,需要综合调度知识来解决.通过梳理发现承载这类函数的载体元素一般是线段、周长、三角、面积等,很自然,在考查动点函数的同时融入了诸多图形的核心知识,处于压轴题的位置成为应然之态.本文通过2016年的中考题作一类析,供参考.
一、线段函数
例1(2016·西宁第10题)如图1,点A的坐标为(0,1),点B是x轴的正半轴上一动点,以AB为边作等腰直角△AB C,使∠BAC=90°,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图像大致是().
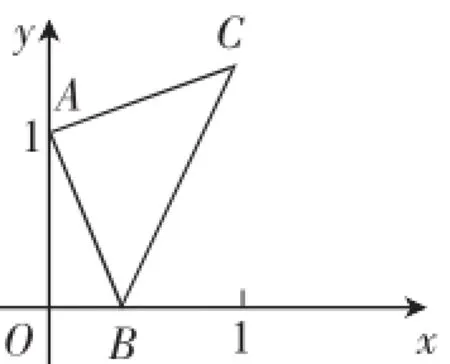
图1
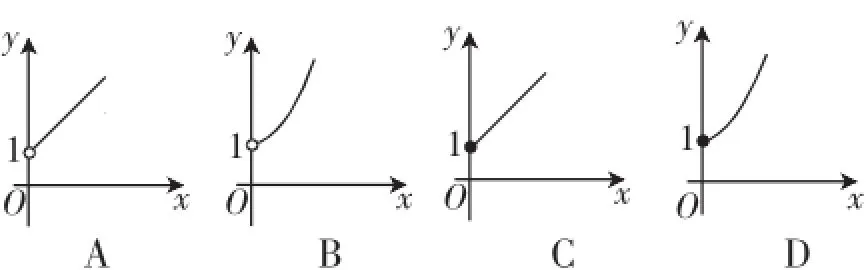
图2
点评:本题以点的坐标为载体,考查动点问题的函数图像.解题的关键是明确题意,把点的坐标与线段关联起来,通过辅助线构造三角形形成对接,隐形考查了三角形的全等,进而建立相应的函数关系式,根据关系式确定的函数类型结合自变量的取值范围判断出正确的函数图像.
例2(2016·泰安第20题)如图3,正△ABC的边长为4,点P为BC边上任意一点(不与点B、C重合),且∠APD=60°,PD交AB于点D.设BP=x,BD=y,则y关于x的函数图像大致是().

图3
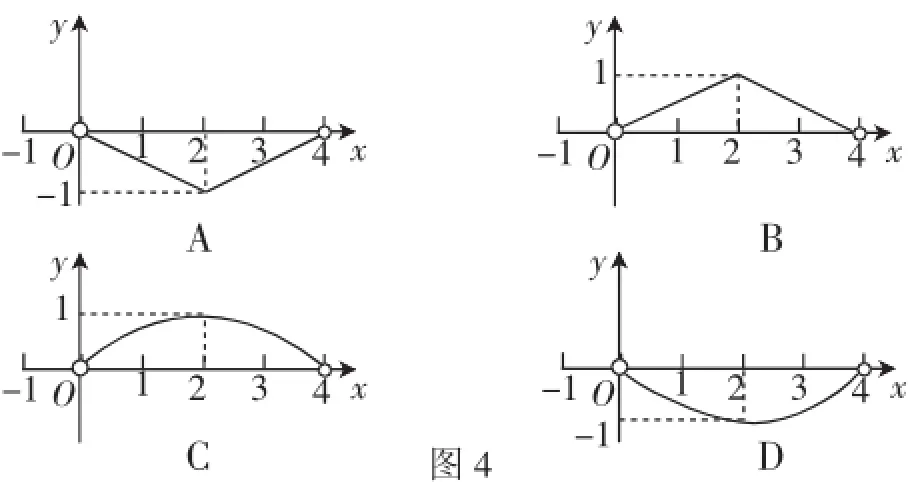
图4
点评:x、y表示的都是线段长,据此可排除A、D,但仍不能确定答案,还需要构建x、y之间的关联.由△ABC是正三角形,∠APD=60°,根据一个常见的相似模型“一线三等角”可证得△BPD∽△CAP,然后由相似三角形的对应边成比例,即可获得函数关系,答案自明.
二、周长函数
例3(2016·衢州市第10题)如图5,在△ABC中,AC=BC=25,AB= 30,D是AB上一点(不与A、B重合),DE⊥BC,垂足是点E,设BD=x,四边形ACED的周长为y,则下列图像能大致反映y与x之间的函数关系的是().
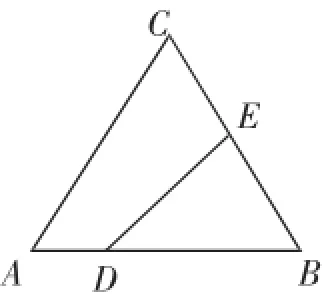
图5
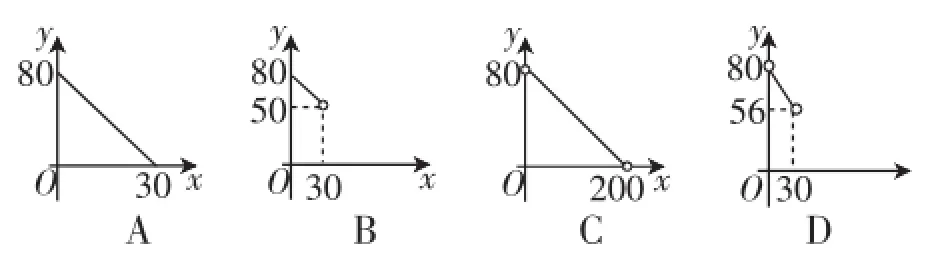
图6
点评:确定y与x的函数关系的关键在于将DE、BE通过x表达出来,而这一关键仍离不开相似性的构造,因此本题综合考查了函数图像、等腰三角形的性质、相似三角形的判定和性质等知识.另外,自变量的取值范围也不容忽视
三、三角函数
例4(2016·烟台市第12题)如图7,⊙O的半径为1,AD、BC是⊙O的两条互相垂直的直径,点P从点O出发(P点与O点不重合),沿O→C→D的路线运动,设AP=x,sin∠APB=y,那么y与x之间的关系图像大致是().
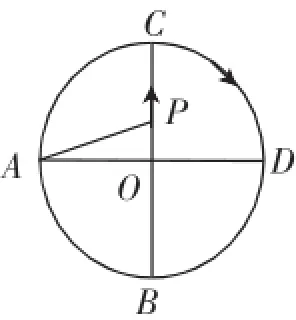
图7
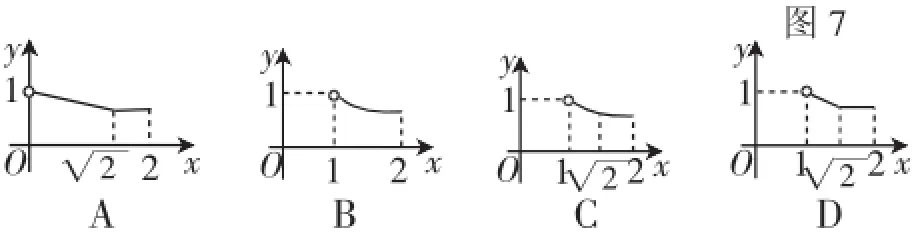
图8
点评:本题有转折点,结合选择支可以估测应该是分段函数,其中转折点是,故根据题意可分1<x<两种情况处理,确定出三角函数y与x的关系式,是解本题的关键,其中第二段结合了圆的核心知识,形成了代数、几何、三角的多重综合.
四、面积函数
例5(2016·济南市第15题)如图9,在四边形ABCD中,AB∥CD,∠B=90°,AB=AD=5,BC=4,M、N、E分别是AB、AD、CB上的点,AM=CE= 1,AN=3,点P从点M出发,以每秒1个单位长度的速度沿折线MB-BE向点E运动,同时点Q从点N,以相同的速度沿折线ND-DCCE向点E运动,设△APQ的面积为S,运动的时间为t秒,则S与t函数关系的大致图像为().
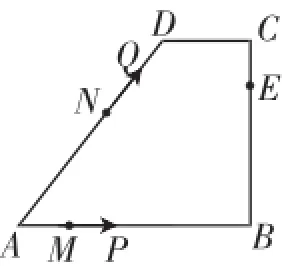
图9
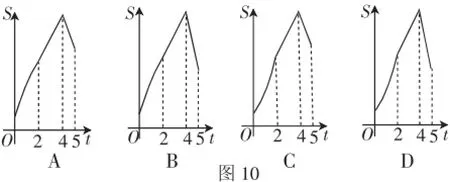
图10
点评:求解析式和排除法相结合可减缩求解历程,作为分段的面积函数有时候全部确定比较麻烦,此时要注意审时度势,看看有无突破口.求出第一段的解析式后即可排除A、B两个选项.而C、D选项的本质差别在于最后的落点与第一段的最高点有高低之别,故而再求出这个终端值即可.
例6(2016·荆门市第8题)如图11,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm),在下列图像中,能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图像是(:).
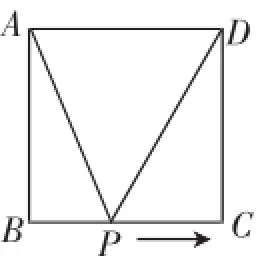
图11
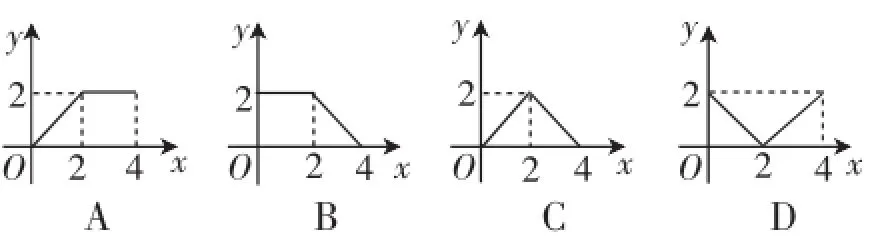
图12
点评:本题作为选择题,通过观察面积走势即可确定.若从求解析式的角度,本题用到的知识点是三角形的面积、一次函数及自变量的取值范围等.
例7(2016·青海省第19题)如图13,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图像大致是(:).
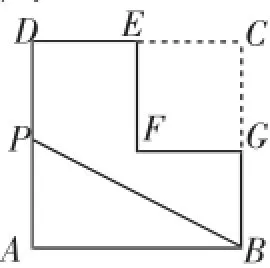
图13
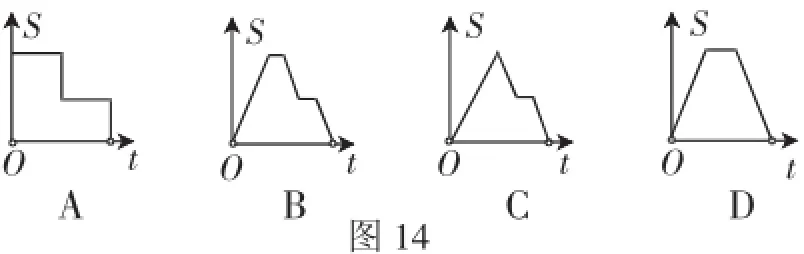
图14
点评:对于本题,没有必要具体确立每一段的函数解析式,只要根据点P在AD、DE、EF、FG、GB上时的不同状态,探测出△ABP的面积S与时间t的变化态势即可.
例8(2016·白银市、临夏州等)如图15,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则下列能大致反映y与x函数关系的图像是(:).

图15
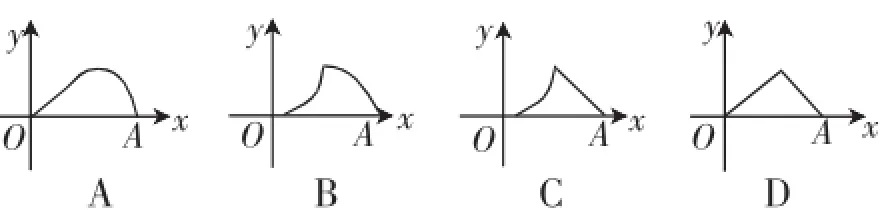
图16
点评:本题单凭走势难以确定,只有具体求出每一段的解析式才能作出判断,其关键仍然是转折点的确定.
结语:四类问题均考查了动点问题的函数图像.函数图像是典型的数形结合,图像应用信息广泛,备受命题专家的青睐,成为选择题中考查学生多种能力的有效载体,综合度大,立意高远,可谓中考的“常青藤”.尤其是面积函数,一般呈分段态势,所以解决面积函数的关键是分类讨论思想的使用,要么具体求出函数关系式,要么观其形态,探其走势,通过排除法确立.
1.邢成云.备受青睐的运动与图像[J].中国数学教育(初中),2016(8).
