明辨特殊与一般,感悟数学小用与大用
——由两道高中自主招考题说起
2017-03-10江苏如皋市长江镇郭园初级中学朱玫瑰
☉江苏如皋市长江镇郭园初级中学 朱玫瑰
明辨特殊与一般,感悟数学小用与大用
——由两道高中自主招考题说起
☉江苏如皋市长江镇郭园初级中学 朱玫瑰
我们知道,不少优质高中自主招生考试往往独立于当地统一中考之外,其命题风格也不同于中考命题原则,往往在初、高中衔接,几何拓展,高中知识改编成初中生能理解的数学语言后,考查学生灵活运用知识的能力.本文选取两道高中自主招生考题,解析思路并跟进命题思考,供分享.
一、两道高中自主招考试题及解析
考题1(2016年江苏省海门中学自主招考题)如图1,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转.若∠BOA的两边分别与函数的图像交于B、A两点,则∠OAB大小的变化趋势为_____(填不变或变大或变小等情形)(以下两者选一小题作答)

图1

图2
思路解析:可以构造图2中的两条垂线段AC、BD.容易根据“一线三直角”得出△BOD∽△OAC,接下来从这两个相似三角形的面积比突破,△BOD的面积是△AOC的面积是它们的面积比为1∶3,所以相似比为即OB,即在Rt△AOB中,tan∠OAB=
变式思考1:如图3,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转.若∠BOA的两边分别与函数的图像交于B、A两点,则∠OAB还是定值吗?

图3
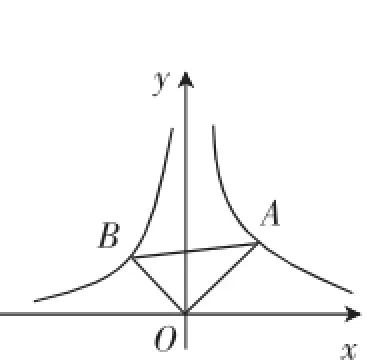
图4
思路解析:类似地,还可作出垂线段AC、BD,分析出两个相似三角形△AOC、△BOD,它们的相似比为1,于是BO∶AO=1,即tan∠OAB=1,即∠OAB=45°.
变式思考2:如图4,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转.若∠BOA的两边分别与函数的图像交于B、A两点,则∠OAB还是定值吗?
走向一般,小结性质:现在让我们“走向一般”,仍然以图4为例,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转.若∠BOA的两边分别与函数和(n> 0)的图像交于B、A两点,则∠OAB还是定值吗?
考题2(2016年江苏省海门中学自主招生考题)(1)类比探究:根据完全平方公式a2-2ab+b2=(a-b)2,可知a
(3)学以致用:某公司为一家制冷设备厂设计生产一种长方形薄板,其周长为4米,这种薄板须沿其对角线折叠后使用.如图5,长方形ABCD(AB>AD)为薄板的形状,沿AC折叠后,AB交DC于点P.当△ADP的面积最大时最节能.

图5
(3)①设AB=x,则BC=2-x.
因x>2-x,故1<x<2.
设DP=y,则PC=x-y.
因△ADP≌△CB′P,故PA=PC=x-y.
由PA2=AD2+DP2,得(x-y)2=(2-x)2+y2⇒1<x<2.当且仅当S取得最大值.1
解后反思:这道考题由特殊到一般,再到应用,让学生在一道试题的求解之后感受到数学追求从特殊到一般的数学精神,也体会到数学知识在生活中应用的广泛性,以及解决问题的力量感(有力地解释了道理,使人彻底信服).
二、关于“特殊到一般”思想的进一步思考
1.理解数学,需要明辨“特殊”与“一般”之间的关系.
数学的本质是什么?众说纷纭,不同的数学家有不同的表达,有说抽象,有说运算,有说数形结合,有说数学思想;就是数学思想,不同的数学家关于分类也有很多层次的探讨.这里不想纠结太多数学本质、数学思想或数学精神,只想结合上述两道“自招”考题,就特殊与一般稍作阐释.进入初中,很多数学概念或性质教学,都力图从特殊走向一般,比如,用字母表示数,图形的抽象等.以上面的两道典型考题来说,当函数解析式中的系数以一个特殊数值给定时,探究相关性质或展开配方、变形,这就是特值引路,而当特殊值不断变式直至参数时,就是一般.学生需要感受考题中从特殊走向一般的这种成果扩大的变化.
2.中学数学已不止于“特殊”,应引导学生走向“一般”.
中学数学与小学数学一个显著不同就是:中学数学引导学生从特殊走向一般.最突出的例子是,初中代数起始阶段就引入了字母表示一个数,而这个数可能是正数、0或负数.很多数学适应性不好的学生容易走不出小学的思维惯习,看到一个数a,习惯认为它是正数,从而在解题中漏解或错解.再比如,对于上面的考题1,在学生解题时,常常是一题一解、一题一得,但是作为教师,在预设该题讲评时,就应该深入下去、对于走向一般,认识到两个反比例函数解析式中的系数k是可以变换的,∠OAB会随着两个系数k的不同取值而随之确定.再比如,对于围长方形这一经典问题背景,给定一个数值的长度围长方形,则围成正方形的面积最大,在学习二次函数之后,学生可以基于二次函数视角,进行有力解释.
3.在“特殊与一般”之后引导学生体会数学小用与大用.
就“考题2”的解题来说,前面两问经历了从特殊到一般的过程,而最后一问回归生活应用,让看似“无用”的数学性质找到了生活中的解释.事实上,恰恰相反,前面关于数学性质从特殊到一般的探究与演算,使得这种数学模型得到严格证明,才保证了在后面生活情境中应用的正确性.从这个意义说,前者是数学之“大用”,后面的生活应用只是数学的“小用”.类似的题例还有很多,比如,函数来源于生活,函数模型可用来刻画很多情境问题,实现问题解决;但函数本身也有其数学上的价值,作为一门重要的数学分支,函数家族成员庞杂,“变量说”反映函数的本质.此外,我们如果能超越解题教学的让学生学会解一道题或一类题的局限,而使学生认识到解这类问题能收获或感悟出来数学的精神、本质、思想或方法,则学生就领略到了数学之“大用”.
三、写在后面
数学自主招生考试领域广泛,命题研究值得深入.是简单的脱离课本、摘选竞赛试题,还是立足课本,将一些教材内容拓展深化?我们还有很多的研究课题值得开展,本文抛砖引玉,期待更多的案例跟进和思考.
1.朱金祥,刘东升.数学教学中例题变式的策略——基于教学追问的视角[J].教育研究与评论(中学教育教学版),2016(9).
2.傅种孙.平面几何教本[M].北京:北京师范大学出版社,1982.
3.郑毓信.“开放的数学教学”新探[J].中学数学月刊,2007(7).
4.中华人民共和国教育部制定.义务教育数学课程标准(2011年版)[S].北京:北京师范大学出版社,2012.
5.罗增儒.数学的领悟[M].郑州:河南科学技术出版社,1997.
6.章建跃.“题型+技巧”的危害[J].中小学数学(高中版),2010(11).
