一道华杯赛决赛几何试题的本质探究

☉广东惠州市惠阳区教育局教研室 钟文辉

一道华杯赛决赛几何试题的本质探究

☉广东惠州市惠阳区教育局教研室 钟文辉

2014年第十九届华杯赛初二组决赛题，是一道有趣的几何“怪”题.它通过旋转图形、变换点和线的呈现顺序，把解题的“捷径”隐藏起来，甚至独辟“曲径”，转移思维焦点，让解题者顺着“曲径”一步步走下去，使一道本应该很简单的题目复杂化.接下来，笔者将顺着这条“曲径”分析问题，而后再跳出“曲径”，沿着“捷径”走向这道题的本质.

如图1，∠ABC=∠BCD=∠DAB=45°，BD=2，求四边形ABCD的面积.

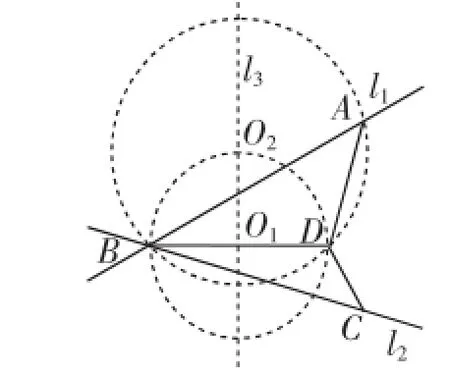
图2

图1

一、题意剖析

1.在变化中寻找不变.

题目言简意赅，“45°”容易让人产生联想，形成思路，但细一想却无从下手，即便有些头绪和猜想，也很难判断是否正确.原因主要有两个：

其一，这不是大家所熟悉的图形，“最底下”的边BC甚至是倾斜放置的.

其二，这不是一个固定的图形，而是一个动图.原因如下：

（1）如图2，固定线段BD=2，过B点分别在BD上方、下方做直线l1、l2，使得l1、l2的夹角为45°.

（2）以BD的中点O1为圆心、BD为直径作圆，交BD的垂直平分线于点O2；以O2为圆心、BO2为半径作圆，交直线l1于点A，易证：∠BAD=45°.

（3）同理，可在l2上找到一点C，使得∠BCD=45°.

由作图过程可知，∠ABD和∠CBD并不是一个确定的值，也就是说，题目中的图形是一个动图.依照题目的意思，这虽然是一个可以变化的图形，但它的面积却是不变的.在变化中寻找不变，这正是这道题最大的难点之一.

2.特殊化寻求猜想.

一个合理的猜想，是解题成功的一半.将变化的图形特殊化，是寻找猜想的捷径，更是深入理解图形的直观方法.

如图3，当∠ABD=45°、∠CBD=0°时，C、D两点重合，

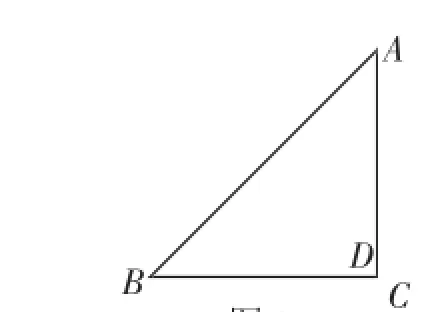
图3

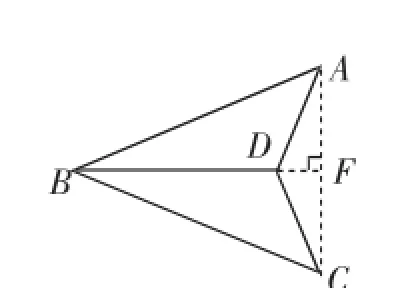
图4

如图4，当∠ABD=∠CBD=22.5°时，连接AC，延长BD交AC于点F，则AC垂直于BD.

从上面两个特殊化的例子中，可以生成两个猜想：1.SABCD=2；2.BD=AC，且BD⊥AC.事实上，已经可以说是本题的答案了，否则，所求面积将不是一个定值.

二、常规解法

对于解一道题来说，从条件出发和从结论出发，是两个最基本的解题思路.

1.从条件出发.

从“∠ABC=∠BCD=∠DAB=45°”这个条件出发，延长AD交BC于点E，形成等腰直角三角形，便是一个很自然的做法.如图5，△ABE和△CDE是两个等腰直角三角形，AE=BE，DE=EC，结合前面的猜想：AC=BD，便可以进一步猜想：△BDE≌△ACE.易证：△BDE≌△ACE，进而易得：BD=AC，且BD⊥AC.从而

注1：本解法是网上广为流传的解法，也是较容易想到的解法.

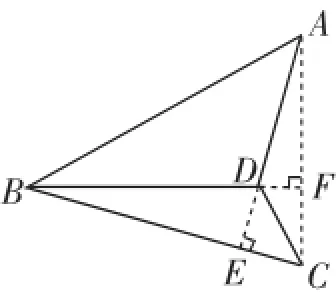
图5

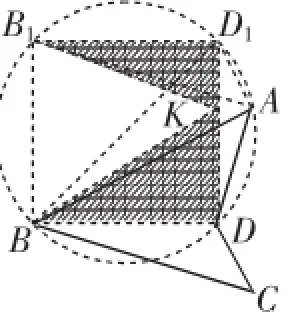
图6

2.从结论出发.

从猜想的结论SABCD=2出发，结合“45°”、图3的特例及猜想“BD=AC，且BD⊥AC”这三个条件，自然便产生这样的解题思路：构造一个“2×2”的等腰直角三角形或正方形，证明等于等腰直角三角形的面积或者正方形面积的一半.

如图6，以BD为边作正方形BDD1B1，连接BD1、AB1、AD1，过A作AK⊥DD1于K，连接BK、B1K.

由∠BD1D+45°=∠BAD，得B、D、A、D1四点共圆.又B、D、D1、B1四点共圆，所以B、D、A、D1、B1五点共圆.

由∠B1AD1=∠B1BD1=45°=∠BCD，B1D1=BD，∠AB1D1=∠D1DA=180°-90°-45°-∠ABD=45°-∠ABD=∠CBD，得△AB1D1≌△CBD.

则SABCD=S△ABD+S△CDB=S△ABD+S△AB1D1=S△KBD+S△KB1D1=

三、巧妙解法

接下来，笔者提供一个巧妙的解法.如图7，延长AD交BC于点E，并旋转图形，使BC“水平放置”，显然，△ABE和△CDE均为等腰直角三角形.

图7

在发现这种解法后，笔者惊叹，这道题真的是出乎意料的简单.而在旋转之后，这个奇怪的图形也变得熟悉起来.当然，发现这个解法并不简单.

第一，在原图中，BC边是倾斜的，这将阻碍解题者产生联想.

第二，想到“求面积”，很多人都会下意识地与“底×高”等价起来，而不是关联起来，陷入了思维定式，于是便不会朝这个方向尝试.

第三，在原图中，BD边是水平的，而且是唯一确定的一条边，于是，解题者的思维焦点便会一直集中在BD上，甚至转移到AC上，而忽略了DE的关键性，容易把四边形ABCD拆分成△ABD和△CBD，但却想不到拆分成△ABE和△CDE的情形.

注2：解法1（或解法2）与解法3结合起来，实际上就是勾股定理的一种证明.此题完全可以放在教材的课后习题中，将解法1和解法3呈现在学生面前，让他们感受全等三角形和勾股定理的一次合作.

四、改编的启示

笔者不是命题者，并不了解命题者的命题思路.但根据上述分析，逆推回去，至少有两种方式，把原图变换成大家熟悉的图形.

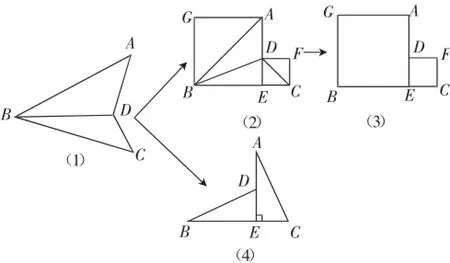
图8

如图8，把DE显示出来，然后把两个等腰直角三角形补充成两个正方形，最后隐藏AB、BD、CD，便形成了图8（2）；把DE、AC显示出来，AB、CD隐藏起来，便形成了图8（4）.

图8（3）是非常经典的一个图形，在小学奥数中常结合面积进行考查，而到了初中又可以证明勾股定理.图8（4）是两个全等的直角三角形，左边的“躺着”，右边的“站着”.

在图8（2）～（4）中，A、B、C、D四点的相对位置关系并没有任何改变，但不仔细观察，却很难发现这三个图形最核心、最基本的构图是一样的.这充分说明，在不改变各点位置关系的情况下，图形的旋转、线段的呈现和隐藏、多余的点的干扰，能够对几何构图形成有效的掩护，让解题者难以看清图形的基本构造.

五、尝试改编

基于前面的探究，笔者思前想后，得到了一系列有趣的改编题，仅供各位读者参考.

1.如图9，△ABE和△CDE均为等腰直角三角形，BD=2，求四边形ABCD的面积.

（说明：此题和原题是一模一样的，只是换了一种表述方法，并且把图形“摆正”了）

2.已知两张等腰直角三角形纸片（或正方形纸片）和一把足够长的有刻度的直尺，请问：至少需要量几次，才能知道两张纸片的总面积？

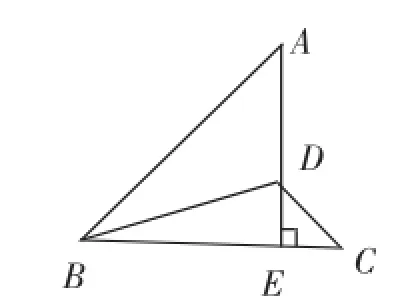
图9

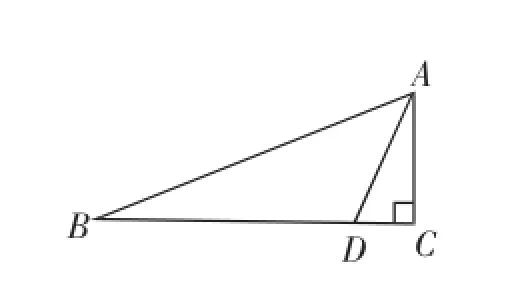
图10

3.如图10，AC⊥BC，∠ABC=22.5°，∠BAD=45°，求证：BD=2AC.

（说明：此图是图4的上半部分，是原题的一种特殊情况）

4.如图11，∠A=45°，∠ACB为钝角，在BC的延长线上取一点D，使得BC=CD，过点D作DE⊥AC于点E，试比较AC、DE的大小.（实际上，AC+CE=DE）

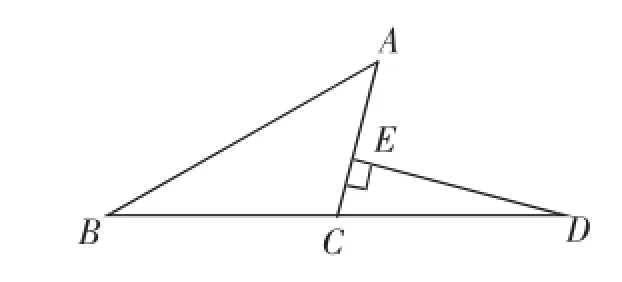
图11

（说明：在图9中，把△CDE去掉，然后以点D为旋转中心，将△BDE沿逆时针方向旋转，使得DE与AD重合，即为图11）

注3：原题是一道垂心背景题，点D是△ABC的垂心.