推陈出新化难点压轴例题显效能

☉江苏无锡市太湖格致中学 陈锋☉江苏无锡市东林中学 杨峰

推陈出新化难点压轴例题显效能

☉江苏无锡市太湖格致中学 陈锋☉江苏无锡市东林中学 杨峰

一、缘起

中考压轴题是中考试卷中综合性强、区分度较为明显的一类试题.它历来是众多学生、教师及命题人员关注的焦点.中考复习，在构建知识网络、进一步夯实基础的同时，如何进一步提高综合性知识复习的有效性，成为每个初三数学教师思考的一个重要课题.下面，笔者就通过对一道关于函数综合问题的典型例题的推陈出新，来谈一谈通过逐次释放例题功效，将例题的成果扩大化，从而化解压轴题难点的一些感悟.

二、题源分析

1.原题再现.

图1

（1）求这条抛物线的函数关系式.

（2）设题中的抛物线与直线的另一交点为C，已知P为线段AC上一点（不含端点），过点P作PQ⊥x轴，交抛物线于点Q，试证明：当P为AC的中点时，线段PQ的长取得最大值，并求出PQ的最大值.

（3）设D、E为直线AC上的两点（不与A、C重合），且D在E的左侧，过点D作DF⊥x轴交抛物线于点F，过点E作EG⊥x轴交抛物线于点G.问：是否存在这样的点D，使得以D、E、F、G为顶点的四边形为平行四边形？若存在，请求出所有符合条件的点D的坐标；若不存在，请说明理由.

2.解法分析.

（1）由于点M和抛物线的顶点N关于x轴对称，从而可得抛物线的顶点坐标为（1，-2），进而得出该抛物线的函数解析式

（2）根据（1）所得抛物线的解析式，可得到点A（-1，0）、B（3，0），进而可求出直线AC的解析式：y=x+1.设P的横坐标为m，从而得到点P的坐标为（m，m+1），Q的坐标为所以PQ=yP-yQ=（m+1）-.根据所得函数的性质即可求出PQ的最大值为及对应的P点的坐标为（2，3），然后判断此时的P点为AC的中点即可.

（3）符合条件的点共有3个，分别为D1（1，2）、

3.效能点评.

这是一道经典的试题，教师每次复习抛物线综合题时都会让学生解，这题对学生思维的考查，逐次递进.对于第（1）问，只要熟悉抛物线解析式的表示方法，在一般式和顶点式之间找到连接点，结合顶点坐标和，抛物线的函数关系式轻松可得.对学生来说，考查的是平时的基本功，难度不大.第（2）问体现了一定的综合性，求抛物线与x轴的交点坐标、求直线AC的解析式，这是对基本功的考验，根据P、Q横坐标相同设出这两点的坐标，再根据图形特征，运用“上纵-下纵”得出PQ的长，运用二次函数的性质，求出PQ的长取得最大值时P的坐标，这里的考查力度开始提升，同时求出AC的中点，发现即为所求得的P的坐标，从而得证.第（3）问的难度进一步提高，对于学生独立画图思考、分情况讨论是一个考验，尤其考验的是学生的计算能力，部分学生在画图和分类讨论能力都具备的前提下算错，其中在解题的状态中无法静下心来展开运算的居多，所以导致第（3）问正确率不高.

三、演绎拓展

在考试中，针对学生对这道试题的解答不是很理想的情况，结合正处于中考第二轮的复习阶段，需要把所有知识整合成一个体系，笔者以此题为基础，创新母题，作为二轮复习课的例题，从几个角度推陈出新，进行拓展演绎，让学生全方位地思考，从而及时巩固并升华.

具体实践方法：

1.“推陈”——把复杂问题简单化.

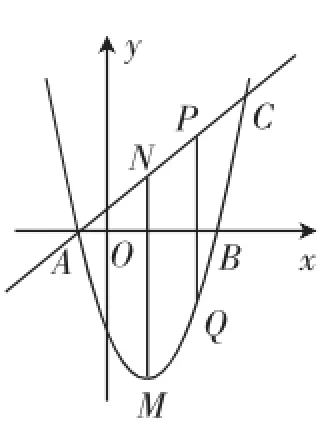
图2

根据学生的思维层次，把原题中所涉及的问题分解为若干个便于操作的知识点，让学生进行尝试：

①求抛物线的表达式；

②求直线与抛物线的另外一个交点C的坐标；

③问：PQ的最大值是MN吗？说明理由；

④在线段AC上是否存在点P，使四边形PNMQ是平行四边形？若存在，请说明理由.

评析：问题①复习二次函数中求解析式的三种方法：一般式、顶点式、交点式；问题②考查交点坐标，即转化为方程组的解；问题③也是本节的亮点：发现点P为线段AC的中点时，PQ最长；对于问题④，需利用数形结合，利用平行四边形的判定：一组对边平行且相等，得到相等，即PQ=MN转化成代数问题来解决.通过对这4个问题的处理，学生的思维能力在解题中获得了提高，同时，也是对原题的复习和巩固.

对不少学生来说，函数综合问题常常使人头疼，往往不知从何下手，有的即使经过教师的一般性讲解，下次再现，学生依然感觉很困难.可见这类问题的难度，也说明教师没有讲透，学生没能真正理解.所以教师在进行压轴题分析的时候，首先要尽可能把题目研究透，把复杂问题简单化，在分解基本图形、提炼解题模型的基础上，教学生理清脉络；同时，在解题分析的时候，要发动学生一起思考，寻找解题的切入点，以启代教；最后，题目的解决并不代表问题的终结，如果想要“入宝山而不空返”，那么必须后续通过设置“姊妹题”进行变式，在复习巩固、提高效率的同时，推陈出新！

2.“出新”——把简单问题新颖化.

（1）“新”在图形.

在问题④的基础上，根据学生的解题状况，我们可以进一步进行拓展，适时进行一次追问：⑤在直线AC上是否存在EF，满足轴，且E′、F′都在抛物线上，四边形EE′FF′是平行四边形？并说明理由.

将问题④和问题⑤结合在一起，原题第（3）问的解题脉络就清晰可见.此时，对原题的思考我们还可以继续下去，通过对问题中“四边形EE′FF′是平行四边形”进行同层次变式，让多种题型在这个母题中“相聚”.

评析：这两小题在各地的中考题中经常可以见到，通常在中考题中会结合其他一些已知条件，考察难度较大.此时作为独立小题出现，学生能集中注意力思考，比较容易突破！当然，四边形EE′FF′也可以改作其他特殊四边形，或改成以E、E′、F、F′为顶点的四边形，甚至可以把EE′∥FF′∥y轴的条件挖掉，此时图形会变得更复杂.作为拓展，可以安排学有余力的学生课后思考，通过对问题深层次的思考，学生无论是对同类问题理解上的通透，还是自身思维层次的提高，都是有巨大影响的.

（2）“新”在面积.

⑦在直线AC下方的抛物线上是否存在一个点G，使得△GNC的面积最大？说明理由.

⑧在抛物线上是否存在点G，使得△ACG与△ACM面积相等？说明理由.

⑨在抛物线上是否存在三个点G，使得△ACG的面积为k？求k的值及点G的坐标.

评析：三角形、四边形的面积的最值历来是中考命题的热点，中考复习也一定会安排最值问题的复习专题.在2010年无锡市中考数学第24题中就出现了与⑦一样的问题.解题方法有多种，一般学生都会考虑把面积表示出来，建立函数，然后用配方的方法求出最值.在面积的处理中，需要分割其中的三角形、四边形，通过解法对比，理解为什么最后选择“过其中一个顶点作x轴的垂线（或作y轴的平行线）”这种方法来解决这类问题，对学生思维的提升很有帮助.同时，这类问题思维的突破，其实已经在前面作“y轴平行线”的多个小问中埋下一颗让思维自然生长的种子.根据问题⑦学生的完成情况，也可以考虑在课后让学生完成它的一个变式：在线段AC上是否存在EF，满足轴，且E′、F′都在抛物线上，使四边形EE′F′F的面积最大？并说明理由.

问题⑧是在前面问题⑦的基础上，在学会这类图形面积求法的基础上向前又继续迈出的一大步.问题看似简洁，其实内涵深刻，如果是想通过将满足条件的直线和抛物线联立来解题的话，那么，要求出位于直线AC上方的情况，这条满足要求的直线解析式如何求出？通过引导发现，结合平行线分线段成比例，结合题目中的现有数据，将问题最终解决的过程，不仅是对前面面积问题的巩固，更是对其他相应知识点应用的一次尝试.

问题⑨是在前面问题⑦⑧的基础上进行进一步拓展，在针对“在抛物线上存在三个点G”这个条件上打开思维，从而转化条件为“作出一条与AC平行的直线，与抛物线只有一个交点”，通过联立方程组，令Δ=0，从而求出第一个点G，继而由前面的面积类问题的解法求出k的值及根据我们对问题⑧的解法求出另外两个点G的坐标.

（3）“新”在隐形圆.

⑩在抛物线上是否存在点E，使得∠CEB=45°？若存在，求出所有满足要求的点E的坐标；若不存在，请说明理由.

11○设MN与x轴交于点D，点E为y轴正半轴上的一个动点，求tan∠DEB的取值范围.

评析：隐形圆问题是中考压轴题中较难的一类.问题⑩是建立在∠CAB=45°的基础上的，此时，只需要作出△ACB的外接圆，即可根据“同弧所对圆周角相等”得出其余满足要求的点E的位置并根据图形求出点E的坐标.问题11○看似简洁，但思维量大.必须通过分析发现：当经过点D、E、B的圆与y轴相切时，∠DEB取得最大值，从而解出tan∠DEB的最大值，其实，这已经是高考的重点——“最大视角问题”.

3.拓展——把问题思维深层化.

12○D在抛物线的对称轴MN上，过点D作与x轴不平行的直线l，直线l与抛物线交于点E、F，若△MEF的内心恰好在直线MN上，求点D的坐标.

评析：此题根据“△MEF的内心恰好在直线MN上”，得“MD平分∠EMF”.在此基础上，进一步去思考如何运用现有条件完成解题.此题对学生的运算能力是一个考验.如果能运用平移的方法，将抛物线平移到顶点为坐标原点的位置，再进行解题，运算量将大大减少，然后把所解得的与点D对应的点的坐标平移回原位置即可.这个问题对学生的运算能力和思辨能力，要求很高，但问题的解决，伴随的是眼界的开阔和能力的提升.

当然，一节课是无法全部完成上述内容的，这需要在一个阶段作为一个复习专题连续进行，利用课内、课外时间，全方位展开.细想这12个问题中所包含的数学内容，甚至是深度，对提升学生的综合解题能力和思维能力大有裨益.如果能把这些内容学透了，函数的问题基本就解决了.这就需要教师课后花更多的精力“钻”进去，学生的学业负担才能真正“减”下来.旧题可以新解，一题可以多解，难题可以巧解，我们应该精做好题，发挥例题深处最大的功效.