创设数学实验彰显几何直观*
2017-03-10安徽无为县刘渡中心学校丁浩勇
☉安徽无为县刘渡中心学校 丁浩勇
创设数学实验彰显几何直观*
☉安徽无为县刘渡中心学校 丁浩勇
随着基础教育课程改革的不断深入,数学课堂教学中发展学生的几何直观能力越来越受到人们的重视.所谓几何直观,就是利用几何图形的直观性来描述和分析问题.《义务教育数学课程标准(2011年版)》(以下简称《标准(2011版)》)的课程内容中已经明确了几何直观是数学课程中的十大核心概念之一.为什么要注重发展学生的几何直观呢?《标准(2011版)》告诉我们,借助几何直观可以把复杂的数学问题变得简明、形象,有助于探索解决问题的思路,预测结果.几何直观可以帮助学生直观地理解数学,在整个数学学习过程中都发挥着重要作用.
数学实验是呈现几何直观的有力工具.在数学实验中,不但可以操作和变换直观图形,而且能将抽象的数学问题直观形象化,提示问题的本质,有利于学生更好地解决问题.
随着科学技术的迅猛发展,现代信息技术为数学实验的顺利开展提供了必备的物质条件和技术保障.充分利用现代信息技术,在数学实验中发展学生的几何直观,是提高数学课堂质量的一种行之有效的途径.
一、借助数学实验呈现几何直观揭示问题的本质属性
在解决某些代数问题时,学生不容易发现其中隐含的数量关系,导致问题很难解决.在这种情况下,可以利用数学实验呈现问题的几何意义,通过几何直观提示问题的本质属性,从而达到问题的顺利解决.
案例1:借助几何图形研究函数问题.
实验操作:(1)如图1,打开几何画板软件,绘制一条长为10的线段AB,过A点在线段AB的上方作长为2的垂线段CA,过B点在线段AB的下方作长为4的垂线段DB.在线段AB上任取一点P,连接CP、DP.度量AP及CP+DP的值.

图1
(2)在线段AB上移动点P,观察CP+DP的大小变化.当CP+DP取最小值时,固定其位置,观察AP的值.
(3)若AP=x,则CP、DP如何用x表示出来?
实验评析:案例1设计数学实验,巧妙地把求函数最小值问题转化成求两条线段的长之和的最小值问题,通过实验操作演示,线段之和的最小值直观、形象地呈现在学生面前,这样学生解决问题就轻而易举了.正如数学家拉格朗日所说:“只要代数同几何分道扬镳,它们的进展就缓慢,它们的应用就狭窄.但是,当这两门科学结合成伴侣时,它们就互相吸取新鲜的活力,从而以快速的步伐走向完善.”因此,数学课堂教学中,要善于开展数学实验,把理性思维直观呈现出来,让学生感悟几何直观,帮助学生建立空间观念,让学生学习看得见摸得着的数学,达到数形完美结合,使数学课堂回归本真.
二、借助数学实验呈现几何直观突出问题的几何背景
数学课堂教学中,有些抽象的数学概念或数学公式,对逻辑思维能力相对薄弱的初中学生来说理解起来比较困难,但是我们可以充分利用信息技术开展数学实验来演示问题的几何背景,突出问题的几何意义,让学生借助几何直观优化对数学概念或数学公式的理解.
案例2:借助几何图形研究平方差公式的几何背景.
实验设计:平方差公式(a+b)(a-b)=a2-b2是多项式乘法运算的特殊情形,运用平方差公式能简化对两个整式的和与两个整式的差相乘的运算问题.为了便于学生更好理解公式,可以借助多媒体设计几何图形利用数学实验对公式进行直观解释.
实验操作:(1)图2是一个边长为a的正方形ABCD,现沿它的一个顶点割去一个边长为b的小正方形,得到一个六边形BCDEFG,如图3.六边形BCDEFG的面积是多少?

(2)沿着GF所在的直线将六边形BCDEFG分割成两个长方形,再把两个长方形按照图4所示的方式拼在一起得到长方形BDEG.长方形BDEG的面积又可以怎样表示?
(3)上述两种方法表示的面积有什么关系?
(4)你能从中得到什么关系式?
实验评析:通过图形拼割的操作实验,利用图形面积的唯一性逐步呈现平方差公式的几何背景.问题(1)引导学生通过割补法求出六边形的面积是a2-b2;问题(2)通过实验演示图形的分割与重组,引导学生得出重新拼成的长方形面积是(a+b)(a-b);问题(3)启发学生思考在图形的分割和重新组合过程中其面积是否会发生变化;问题(4)引导学生根据面积的不变性得出平方差公式:(a+b)(a-b)=a2-b2.
数学家华罗庚说过:“数与形,本是相倚依,焉能分作两边飞.数缺形时少直觉,形少数时难入微.形数结合百般好,隔裂分家万事非.切莫忘,几何代数统一体,永远联系,切莫分离!”本例通过生动、形象的图形拼割实验让学生体会平方差公式的几何意义,体现了代数与几何之间的内在联系和统一,不仅可以帮助学生有效地记住平方差公式,还可以促进学生对平方差公式的直观理解.
三、借助数学实验呈现几何直观转换数学语言的表现形式
数学语言是数学思维活动的载体,它是由数学符号、数学术语、数学图形等经过人脑加工改进的科学语言.数学语言主要有三种表现形式,即文字语言、符号语言和图形语言.
有的数学问题是由文字语言描述的,表述虽然简洁,但其高度的抽象性也给学生理解带来一定的困难,不利于问题的解决.如果我们把文字语言转化为用直观的图形语言来呈现,这样会便于学生观察与联想,有益于学生对问题的解决.
案例3:借助几何直观研究解方程(组)的实际应用问题.
我国古代《算法统宗》里有这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.试问房客各几何?
实验设计:本题是由七言律诗的形式呈现的,文字虽然精练,但不利于学生寻找其中的等量关系.为了便于学生理解题意,可以将文字语言转化成图形语言,让学生在直观中明晰.
实验操作:(1)当一房住七客时,如图5,画一个长方形ABCD,其中长度AB表示实有房间数,高度AD表示每个房间里住的房客数.增加几个房间众客可以全部入住?如图6,延长AB至E,使BE=1,作长方形AEFD.长方形AEFD的面积与众客人数有什么关系?
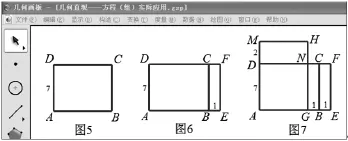
(2)当一房住九客时,如图7,在图6的基础上画长方形AGHM,其中长度AG表示实有房间数,高度AM表示每个房间里住的房客数.则DM等于多少?AB比AG大多少?
(3)由众客人数的不变性可知长方形GEFN的面积与长方形DNHM的面积有什么关系?
(4)由(3)可知AG的值是多少?则实有房间数(AB的值)是多少?众客数是多少?
实验评析:案例3用长方形的长度表示房间数,用长方形的宽度表示每个房间的住客数,从而长方形的面积赋予的含义就是众客的人数.这样根据面积的不变性得出房间数和房客数就非常容易.正如数学家斯蒂恩所说:“如果一个特定的问题可以被转化为一个图形,那么,思维就整体地把握了问题,并且能创造性地思索问题的解法.”因此,我们在解决数学问题时,要善于进行数学语言的转化,灵活地把用文字语言或符号语言描述的抽象的数学概念和数量关系转换为形象化、简单化的图形语言,为解决数学问题开辟一条崭新的途径.
四、借助数学实验呈现几何直观赋予数值几何意义
心理学家皮亚杰根据儿童的认知理论将儿童的认知分为四个阶段,即感知运动期、前运算思维期、具体运算思维期和形式运算思维期.初中学生的认知开始从第三阶段过渡到第四阶段,其思维形式刚刚摆脱思维内容,思维的深度和广度非常匮乏.针对学生的这一特征,对一些较难理解的数量关系,如果能通过实验验证的方法,借助几何图形使这些数量关系直观形象化,那么就很容易找到解决问题的方法.
案例4:借助几何直观比较实数的大小问题.
实验操作:(1)打开几何画板软件,如图8,绘制一个每个小正方形的边长都为1的8×6的网络图.
(2)在网络图内分别绘制线段AB、BC、CD、AD.线段AB、BC、CD、AD的长度分别是多少?

图8
(3)AB+BC+CD与AD有什么大小关系?
实验评析:本例通过构造特定长的线段来表示对应的实数,利用几何直观非常容易解决问题.数学家克莱因指出,“数学不是依靠于逻辑,而是依靠正确的直观,数学的直观就是对概念、证明的直接把握.”因此,数学课堂教学中,要善于培养学生构造图形来解决问题的意识,逐步形成一种遇到抽象性的数学问题之后,会主动运用几何直观的思维方式展开数学思考.
总之,几何直观不仅是一种数学意识,也是一种思考问题的能力和技巧,更是一种数学的思维方式.教学中,要充分利用信息技术开展数学实验活动,适时呈现几何直观,使抽象思维同形象思维结合起来,突出问题的主要线索,充分展现问题的本质,从而达到顺利解决问题的目的.
1.中华人民共和国教育部.义务教育数学课程标准(2011年版)[S].北京:人民教育出版社,2011.
2.丁浩勇.利用信息技术在数学实验中开展概念教学[J].中学数学(下),2016(4).
3.丁浩勇.利用信息技术在数学实验中深化学生的数学思想[J].数学通讯(教师刊),2016(6).
*本文系基金项目:安徽省教育信息技术研究“十二五”规划2015年立项课题“现代教育技术环境下的数学实验教学研究”(AH2015056)的研究成果.
