深刻理解习题结构，跟进变式拓展追问<br/>——以圆为背景的综合题改编例说

深刻理解习题结构，跟进变式拓展追问
——以圆为背景的综合题改编例说

2017-03-10浙江宁波市曙光中学王海燕

中学数学杂志 2017年2期

☉浙江宁波市曙光中学王海燕

深刻理解习题结构，跟进变式拓展追问
——以圆为背景的综合题改编例说

☉浙江宁波市曙光中学王海燕

近读文1，文中提到：“经验教师常常重视对例题进行恰当改编，拓展追问，使得例题的教学功能大为增强，有效提高课堂教学效果.并且结合具体的改编题例阐释了常用的习题变式策略：简单改编、置换设问、增设铺垫、拓展生长.主要目的是面向全体、渗透方法、润物无声、鼓励挑战.”笔者深受教益，在近期中考复习时也注重对一些例题或习题进行改编变式，丰富题目的教学与训练功能.本文整理以圆为背景的综合题，解读改编试题的意图与教学立意，并跟进思考，供研讨.

一、以圆为背景的综合题例解读

题例1如图1，以Rt△ABC的直角边AB为直径作⊙O，交斜边AC于点D，点E为OB的中点，连接CE并延长交⊙O于点F，点F恰好落在弧AB的中点，连接AF并延长与CB的延长线相交于点G，连接OF.

（1）求证：BG=2OF；

（2）求证：BG=2BC；

（3）求sin∠BAG的值；

（4）求sin∠ACB的值；

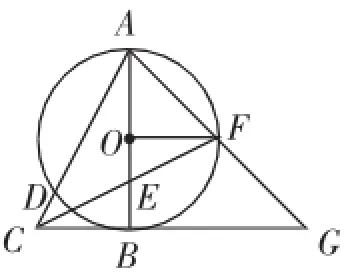
图1

（5）若⊙O的半径为2，求△ACG的周长.

改编解读：本题由2016年山东聊城中考题改编而来.由该题的条件可解读出OF是△ABG的中位线，△OEF≌△BEC，于是前两问可顺利突破；而发现特殊的等腰直角三角形△ABG是破解第（3）、（4）问的关键；沿着前面的思考，增设强化条件圆的半径之后，△ACG的三边都可解出.这样5个小问训练下来，可以加深学生对这类图形结构的理解，使得围绕该图或条件设计出来的不同问题都达到训练效果.

题例2如图2，半径为5的⊙O中，直径AB的不同侧有定点C和动点P.已知sin点P在弧AB上运动，过点C作CP的垂线，与PB的延长线交于点Q.

（1）求AC的长；

（2）求证：△ABC∽△PQC；

（3）当点P与点C关于AB对称时，求PQ的长；

（4）当点P运动到什么位置时，CQ取到最大值？求此时CQ的长；

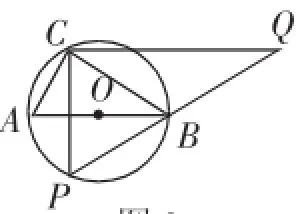
图2

（5）当点P运动到弧AB的中点时，求CQ的长.

改编解读：这道题的出发点和关键是△ABC∽△PQC，第（3）、（4）问主要训练学生转化思路，把对△CPQ的研究转化到△ABC中；第（5）问将思路转化聚焦在△APC中，首先要定位点P是半圆AB的中点，然后△APC中有特殊角度（∠ACP=45°），当CP被突破之后，再根据比例关系对应得出CQ的长.

题例3如图3，直线l与⊙O相切于点D，过圆心O作EF∥l交⊙O于E、F两点，点A是⊙O上一点，连接AE、AF，并分别延长交直线l于B、C两点.

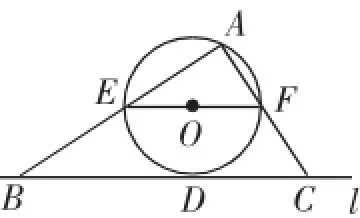
图3

（1）小明发现∠ABC与∠ACB是互余关系，请直接指出“小明发现”的真假.

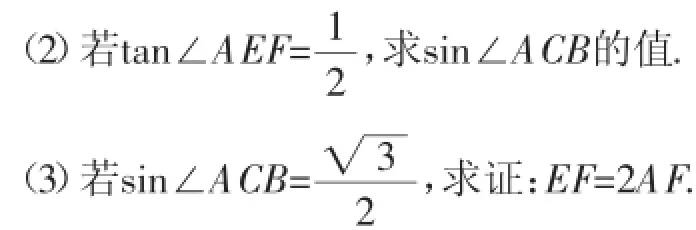
（4）当⊙O的半径r=5，BD=12时，

①求tan∠ACB的值；

②求AB或BC或AC的长.（三选一，简述步骤即可）

改编解读：第（1）问起热身作用，让学生感受图3中的互余关系；第（2）、（3）问所给的两个锐角三角函数值分别对应着两种不同形状的直角三角形，训练和教学的目的是引导学生注意明辨；最后一问需要构造直角三角形，研究此时图形中所有直角三角形的形状，只要过点E作EH⊥BD于H，连接OD，就可将问题转化到△BEH中实现问题突破；最后一问较有挑战，因为不论求哪一条边长都需要较繁杂的运算，如果能熟练利用锐角三角函数值辅助运算，可以适当简化，训练时先让学生经历求解，然后优化、简化，体会数学求简的追求.

题例4如图4，AB是⊙O的直径，PA、PC分别与⊙O相切于点A、C，PC交AB的延长线于点D，DE⊥PO交PO的延长线于点E.

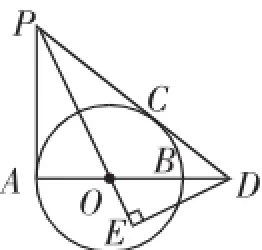
图4

（1）求证：△APO∽△EDO；

（3）在（2）的条件下，直接判断DE与圆O的位置关系；

（5）在（4）的条件下，求△POD的外接圆的直径.

改编解读：第（2）、（4）问中的两个锐角三角函数值分别对应着不同的直角三角形，通过并列设问，引导学生注意辨析，在（2）的条件下会出现特殊角度30°，此时点E成为圆O上的一点，DE也特殊化为圆O的切线；第（4）问强化“tan∠APC=”后，图形中直角三角形有两种重要的形状，即“3，4，5”或“1，2的形状，解读出这两种形状后，对于第（4）问求解很关键；最后一问并不需要构造△POD的外接圆，可以根据教材上的拓展题（正弦定理）来获得快速突破，因为∠ADP的正弦函数值可以在△APD中思考，而△OPD的三边都容易求得.

二、习题改编变式的进一步思考

1.深刻理解习题“深层结构”是改编的前提条件.

与数学概念教学一样，首先教师本人要对数学概念有深刻的理解，比如，教学数轴时，在一个数学老师眼中，数轴不只是“三要素”这么简单，数学承载的是数、形结合，是后续两点间距离公式的平台，是从“一维数轴”发展到“二维平面直角坐标系”的生长，是数与点一一对应、连续性的理解平台，等等.所以在改编习题时，需要对习题的深层结构有深刻的理解，如果教师本人只是初步对问题的思路获得了贯通，而没有明辨问题的深层结构，是不容易想到如何改编的；如果没有想清楚问题的真正难点，就不知道在哪些地方设计铺垫式问题；如果没看清问题结构，就难以将问题沿着这个结构再向纵深处拓展、变式、生长.

2.习题改编要明辨重点，突破难点.

在深刻理解习题的基础上，要认真思考习题的重点、难点所在，接着在这些重、难点之处进行细化，通过一些铺平垫稳式的系列设问，使得难点突破变得自然、合理.比如上文题例2中，这道考题常常会以一道填空难题的方式出现，直接求第（3）或（4）问，这时的难点就在于学生能否发现和利用第（2）问，将问题有效转化.比如，题例4中，原题“tan∠APC=”是在总题干中，为了引起学生重视这个强化条件的价值，我们先设计了第（2）问，让学生感受到随着锐角三角函数值的变化，三角形的形状会发生变化，图形位置会发生变化，保持对这些锐角三角函数值的敏感，发现特殊直角三角形将起到突破性作用.

3.习题改编要照顾全体并鼓励少数高层次学生向上挑战.

从文中提供的4个题例来看，我们都安排了5个小问，其中第（5）问极具挑战性，根据我们的教学实践，在限时15分钟左右答题时，只有前20%的学生才有机会挑战满分（我们一般按每个小问20分批阅），这样改编、设问、评价的目的正是照顾全体并鼓励少数高层次学生向上挑战的命题意图.其他学生在限时内没有答对，还可以后续订正时再深入思考，直至弄懂.