追求自然、简约、深刻的思维课堂
——以直角三角形的性质复习课为例
2017-03-10浙江省平阳县水头镇第一中学张合远
☉浙江省平阳县水头镇第一中学 张合远
追求自然、简约、深刻的思维课堂
——以直角三角形的性质复习课为例
☉浙江省平阳县水头镇第一中学 张合远
随着新课程的进一步深入,教师的教学理念、教学方式发生了很大的变化,课堂也从改革初始的尝试变得日益成熟,特别是复习课教学,从追求课堂的大容量教学转向简约,复习模型从“题海战术”转变为“一题(图)一课”.近几年,浙江省特级教师张宏政名师网络工作室活动特别提倡“一题(图)一课”的复习课教学模式.2016年11月21日,2016之秋第109届浙派名师暨省初中数学名师网络工作室课堂教学艺术展在杭州师范大学隆重举行.笔者作为浙江省张宏政名师网络工作室的学科带头人,为与会的1000余名教师展示了一堂八年级“直角三角形的性质复习”的观摩课,得到观摩老师的一致好评.本文记录该课的教学设计与教后反思,与更多的同行分享与研讨.
一、教学简录及分析
(一)提供背景图形,生成相关知识.
引入:我们知道,三角形按角分类,可以分为锐角三角形、直角三角形和钝角三角形.由于直角三角形的特殊性,它在日常生活与今后的学习中有着广泛的应用.今天我们专题复习“直角三角形”(板书课题).请大家看问题1.
设计说明:这节课由三角形的分类与直角三角形的特殊性引入,旨在使学生明确直角三角形在整个“三角形”知识单元中所占的位置和广泛应用,从而激发学生复习的兴趣和要求.
问题1:如图1,在△ABC中,∠C=90°,你能得出哪些结论?
设计说明:从一个低起点问题引题,旨在让更多的学生参与到课堂中来,同时,也可以从角、边入手梳理直角三角形的有关知识,为下一环节的顺利展开铺平道路.
板书:角与角:∠A+∠B=90°,边与边:a2+b2=c2.
师:下面给出具体数据,请你们求这个三角形的面积.
问题2:如图1,在△ABC中,∠C=90°,AB=10,你能求出△ABC的面积吗?
生:不能求出△ABC的面积.
师:为什么?
生:这个三角形是不确定的.
师:哦?那就请你们再添加一个条件解决这个问题.
请添加一个条件,再解答下题:
如图1,在△ABC中,∠C=90°,AB=10,_________,求△ABC的面积.
……
师:今后我们还会进一步学习任意锐角度数的直角三角形三边之比(.引导学生添加斜边上的高线)若点D为AB边上的一个动点,请大家看问题3.

图1

图2
问题3:如图2,在△ABC中,∠ACB=90°,AB=10,BC=6,若点D为AB边上的一个动点,则线段CD的取值范围是多少?为什么?
板书:面积法.
师:看来面积法是解决几何问题的一种有效方法.求斜边上的高线CD,是否还有其他方法呢?(勾股定理)
板书:设元构建方程模型.
师:点D还有哪些特殊位置值得研究?这时CD的长分别是多少?为什么?
生:中线与角平分线.
板书:直角三角形斜边上的中线等于斜边的一半.
生:当CD为角平分线时……(说不下去了)
师:哦,好像遇到困难了.请想一想,角平分线有什么性质?
生:过点D分别作BC、AC的垂线段DE、DF(如图3).则DE=DF,这时,△CDE为等腰直角三角形,所以CD=,但DE的长为……(说不下去了)
师:请同学们思考,这么多的高线,你们能联想到什么方法呢?
生:面积法.
师:看来,能否对条件中隐含的信息进行充分挖掘是解题的关键.下面我们改变题目中CD的位置(出示变式题).

图3
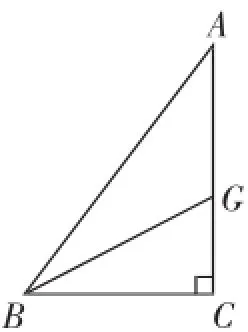
图4
变一变:如图4,若上述条件均不变,把∠C的平分线CD改成∠B的平分线BG,则BG的长为多少?
师:刚才的方法还适用吗?
设计说明:通过设计开放性问题求面积,进一步复习勾股定理的应用、特殊三角形中边角之间的关系,而后自然引出特殊线段的长度求解,既复习了它们的性质,也可以让学生体验面积法、方程思想等解决问题的方法.
生:仍然可用面积法.
师:看来面积法在解决问题中具有普遍性.是否还有不同的方法呢?
生:可以利用勾股定理.
师:利用勾股定理构建方程模型也是重要的解题思路.当然,有时还需要先通过(轴对称)变换,把条件聚集到同一个三角形中.
师:好了,我们从角、边、重要线段入手梳理了直角三角形的相关知识,同时对解决问题的方法也有了进一步的体验.下面让我们继续探究.
(二)建立图形间的联系,体验数学思想.
问题4:如图5,在△ABC中,∠ACB=90°,AB=10,BC=6,点G是边AC上的一个动点.记点A关于直线BG的对称点为A′,连接GA′、BA′,BA′与边AC交于点E.若△A′GE为直角三角形,求AG的长.
分析条件,引导学生画出如下分类图形(如图6,图7)并解答:
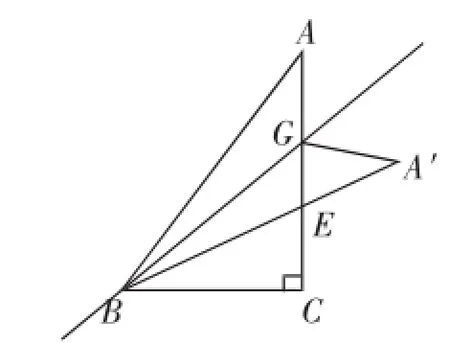
图5
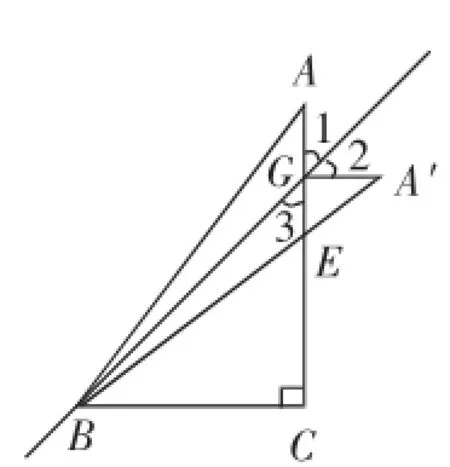
图6
方法二:根据轴对称得∠1=∠2=∠3=45°,故BC= GC=6,此时AG=2.
课堂预设:
(1)如图6所示,当∠A′GE=90°时,
方法一:根据轴对称得

图7

图8
方法三:如图8,过点A′作A′F⊥BC交BC的延长线于点F,则∠A′FB=90°.易得四边形A′GCF是矩形,CF=A′G,A′F=CG.设AG=A′G=x,则BF=BC+CF=6+x,A′F=CG=ACAG=8-x.在Rt△A′FB中,由勾股定理得(6+x)2+(8-x)2= 102,解得x1=2,x2=0(舍去),此时AG=2.
(2)如图7所示,当∠A′EG=90°时,
方法二:点C与点E重合,则A′E=A′B-BC=10-6=4.设AG=A′G=x,则CG=AC-AG=8-x.在Rt△A′GE中,由勾股定理得(8-x)2+42=x2,解得x=5,此时AG=5.
综上所述,AG的长为2或5.
归纳:本题主要考查直角三角形的综合应用,以及点的运动带来的图形变化问题.探讨有关直角三角形的问题,要注意进行分类讨论;在对待动点问题时,耐心画出各类情况对应的图形,可达到事半功倍的效果(切忌所有情况画在一个图中).根据问题4,你还可以提出哪些问题?
教师备用以下拓展探究问题,如果学生思维活跃就随学生的问题展开,否则教师尝试抛出如下拓展探究问题引发学生思考.
课堂预设:
策略一:不改变任何条件,学生可能得出新问题;
与面积有关的结论:若S△AGE=S△BCE,求AG的长.
……
策略二:改变条件探求是否有新问题.
减弱条件探求是否有新问题:线段AC改为射线AC,线段BC改为直线BC,探求点A′的位置;另外,把图4放在平面直角坐标系中还可继续拓展.
……
设计说明:通过对问题的进一步变化,既强化了对运动观下几何问题的本质把握,也使学生加深了对分类讨论、面积法、构建方程模型等基本数学思想方法的体验与感悟,而后面尝试让学生提出问题,则旨在培养学生的问题意识,初步感受提出问题的策略.
(三)感悟数学思想,启迪学生智慧.
拓展探究:如图9,在△ABC中,∠ACB=90°,AB=10,BC=6,点G是射线AC上的一个动点.记点A关于直线BG的对称点为A′,连接GA′、BA′,BA′与射线AC交于点E.当点A′落在直线BC上时,求AG的长.
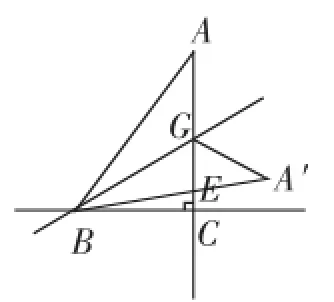
图9
引导学生画出如下两种分类图形(如图10、图11),并用面积关系和勾股定理等方法建立方程模型解答此题.
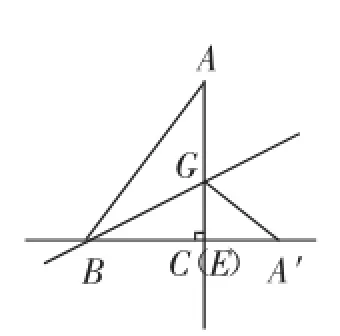
图10

图11
设计说明:通过对问题的进一步改编,为学生认识图形、把握本质创造了思维的载体,也为分类讨论、方程模型思想的灵活运用与概括提供了必要的逻辑通道.
检测练习:如图12,有一张直角三角形纸片ABC,AB=10,BC=6,现将直角边AC沿直线AP折叠,使它落在斜边AB上,且与AD重合.你能求出CP的长吗?
变式1:如图13,在Rt△ABC中,∠C=90°,BC=6,AB= 10,若AB上有一点M,AC上有一点N,AM=CN,折一折,算一算,你能否找到这样的M、N,使△AMN是直角三角形,且满足MN=4?若存在,请求出AM的长;若不存在,请说明理由.

图12

图13
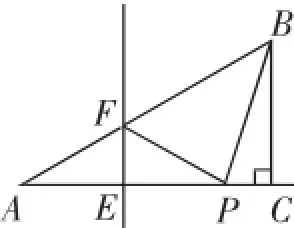
图14
变式2:如图14,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=6.点E是AC边上的一个动点(不与点A、C重合),过点E作EF⊥AC交AB于点F,将∠A沿直线EF翻折,点A落在射线AC上的点P处.当△BFP为直角三角形时,求AE的长.
设计说明:通过这组变式训练题,既巩固了当堂复习的有关知识和解题策略,又培养了学生的逻辑思维能力.
二、教学反思
本节课以一个简单的基本图形引题,旨在发动更多的学生参与课堂,通过问题串的设计与变式教学逐层推进,提倡多角度、多策略解决问题,注重在合作交流中让学生倾听、优选,在获得解题思路的同时不忘归结能力、发散思维的培养,体验并尝试如何提出问题,初步掌握提出问题的若干策略.
为了追求自然、简约、深刻的思维课堂,这节课的教学过程得到了整体优化,调动了全班学生学习的积极性,体现了新的教育理念和当前的课改方向,取得了满意的教学效果,听课的教师给予了很高的评价.大家一致认为这节课的主要特点是:
1.去繁为简,一图贯之.
用一个图形贯穿始终,并按照由浅入深、层层深入的设计思路展开,其中开放性问题的设计、动点元素的渗透及设问形式的变化,赋予了本课灵动与生机,也有效提高了课堂中高认知思维的含量.
2.提炼方法,生长智慧.
复习课的重要目标,就是要让学生在梳理知识的同时,感悟数学解题策略,提炼基本数学方法,从而达到生长智慧的目的.因此,从问题2中的求三角形面积到问题3中的求CD的取值范围,为面积法的引出进行了必要的铺垫,也影射了数形结合的重要性,而后面求角平分线长度的设计,对这一几何基本大法予以强化,同时也自然生成了建构方程模型的解题策略.而问题4用动点沟通图形联系的设计,既体现了复习课的综合性要求,也为分类讨论、方程模型思想的运用与概括提供了逻辑通道.本课提倡多角度解决问题,并在比较中优化思路,突出本质,同时尝试提出问题,初步体验提出问题的若干策略,从而达到梳理知识、理解方法、形成能力的教学目标.
初中数学复习课,教师应从一道题目(一个基本图形)出发,开放性地设计问题,鼓励学生从多角度解决问题,并尝试让学生自主编题,提出问题,为后续进一步挖掘题目作铺垫.同时关注学情,动态生成,让课堂更加自然、简约、深刻.在这样一条复习主线下,提炼解题策略,挖掘数学不变的量,渗透数学思想方法,真正让数学复习课成为学生的主阵地,走出“题海战术”,追求“简约”却不简单的课堂,体现“一题(图)一课”的价值,真正凸显“以生为本”的教学理念.
1.中华人民共和国教育部制定.义务教育数学课程标准(2011年版)[S].北京:北京师范大学出版社,2012.
2.顾泠沅主编.初中数学教学研究[M].上海:上海教育出版社,2012.
3.吴立建.数学课堂中应重视引导学生提出问题[J].数学通报,2013(7).
