中、新初中数学教科书中“相似图形”的比较研究

☉浙江师范大学教师教育学院师晓莉朱哲王安

中、新初中数学教科书中“相似图形”的比较研究

☉浙江师范大学教师教育学院师晓莉朱哲王安

一、前言

课程是引起学生差异的一个关键因素，尤其是教科书，对学生成绩存在着潜移默化的影响.通过对不同国家教科书内容的比较，可以了解学生在数学学习过程中的不同经历，以及这种差异对学生学习产生的影响.几何课程在中学阶段具有重要的地位和作用，是训练学生思维、发展学生演绎能力的基础课程.近年来，新加坡学生在国际数学和科学测试（TIMSS）中的优秀表现，一直受人瞩目.本文选取新加坡与中国初中数学教科书中共有的章节“相似图形”进行比较，寻找两者的异同，以期对我国数学教科书的编写与实施产生积极的影响.

二、研究准备

1.中国与新加坡数学课程的核心.

中国《义务教育数学课程标准（2011年版）》［1］（以下简称《标准》）指出，义务教育的数学课程是培养公民素质的基础课程.数学课程的核心是让学生掌握必要的基础知识和基本技能，培养学生的抽象思维和推理能力，培养学生的创新意识和实践能力，促进学生在情感、态度和价值观等方面的发展.义务教育的数学课程能为学生未来生活、工作和学习奠定重要的基础.

新加坡数学课程设计是以“五边形”为核心思想［2］，在五边形中间的是“数学问题解决”，它意味着在新加坡，问题解决是数学教育的中心.问题解决的能力依赖于其他因素，而其他因素就体现在五边形的五条边上：概念、技能、过程、态度和元认知，也就是“数学问题解决=（概念、技能、过程、态度、元认知）”.

2.内容的选择.

本文选择人民教育教育出版社义务教育教科书《数学》［3］中九年级下册第二十七章“相似”与新加坡数学教科书New Syllabus Mathematics2（7th Edition）［4］第二册第七章“全等和相似”中的“相似”部分进行分析、比较，以期对我国数学教科书的编写产生一定的启示.

3.比较的方法与维度.

笔者采用文本分析法，定性和定量相结合，分别剖析两种教科书中“相似”的内容.本文主要从表层和内在两个方面对两种版本教科书中的“相似”内容进行比较.第一个层面，包括内容编排和内容呈现两个维度；第二个层面是对学生能力培养的比较，包括逻辑思维能力、综合应用能力的培养两个维度.最后，得出启示.

三、教科书内容的比较

中、新教科书在内容上存在很大的差异，本文分别从内容的编排与侧重点和内容的呈现两方面进行论述.

1.内容的编排与侧重点.

中、新教科书中关于“相似”知识的编排如表1所示.

表1 中、新教科书中“相似”的编排

从表1可以看出，两本教科书中“相似”部分的设置仍然存在一定的差异.《数学》的重点部分为“探究相似三角形的判定定理，并应用定理判定三角形是否相似”.除此之外，其第三节“位似”，是相似与坐标的结合.该部分内容在相似的基础上，结合图形的位置关系，要求学生能熟练应用位似比、位似中心解决相关问题.“位似”的引入是综合性知识在教科书中的呈现，综合性知识有利于学生将所学知识融合在一起，促进学生数学思维的发展，提高学生的数学素养.这与我国《标准》中所强调的要体会数学知识之间、数学与其他学科之间的联系相适应.

New Syllabus Mathematics中的重点部分是“放大（或缩小）图的应用”，包括应用相似比画出放大（或缩小）图和解决地图中距离与实际距离关系等问题.教科书中呈现出3个探究、7道例题详细讲解这些问题应该如何解决，并配有相关的练习题以供学生巩固.而《数学》中，仅仅在练习和课后习题部分分别出现一道与比例尺有关的计算问题，并没有通过例题的形式展示该类问题的解法.

2.内容的呈现.

（1）知识的引入、展开和总结.

《数学》的前言部分，“在现实生活中，我们经常见到形状相同的图形，如国旗上大小不同的五角星、不同尺寸同底版的相片等.在‘全等三角形’一章中，我们研究了形状和大小完全相同的两个三角形的性质和判定方法.类似地，两个形状相同、大小不同的三角形，它们的边和角有什么关系？如何判断两个三角形的形状是否相同？如何按要求放大或缩小一个图形呢？

要回答上面的问题，就进入这一章的学习吧！在实验、探究和论证之后，你就能得到问题的答案.”

前言从生活中常见的例子引入，然后逐步导向与本节课内容相关的问题，引发学生思考，最后提出“要回答上面的问题，就进入这一章的学习吧”.这样设计，不仅使数学更加贴近生活，同时激发学生探索数学的热情和动力.在章节复习部分，首先通过知识框架图的形式帮助学生构建知识体系，然后通过问题引导学生思考，查漏补缺［5］.

New Syllabus Mathematics的前言部分，明确列举出学习本章需要达到的基本目标，使学生能有的放矢，从而提高学习效率.在章节复习部分又回扣前面的目标，进行归纳总结，将本章所涉及的知识点一一列举，完善知识体系.

New Syllabus Mathematics中知识展开环节中设有的模块包括“小组讨论”“调查研究”“思考时间”“例题与详解”“课堂练习”.其中特色最鲜明的是其对例题的展示，主要体现在以下几个方面：一是例题涉及的知识明确，指向性强，每道例题旁边都标注有该题涉及的知识点；二是例题的解题步骤明确，利于学生模仿；三是例题后有同类型的习题，供学生巩固练习，有利于促进学生对新知识的理解和运用.《数学》中也设有“例题和习题”，但相对于New Syllabus Mathematics，《数学》的不同之处主要表现在：一道例题对应多种类型的习题，增加学生学习的困难.

例如，《数学》27.1“图形的相似”中的例题和练习如下：

例如图1，四边形ABCD和EFGH相似，求角α、β的大小和EH的长度.

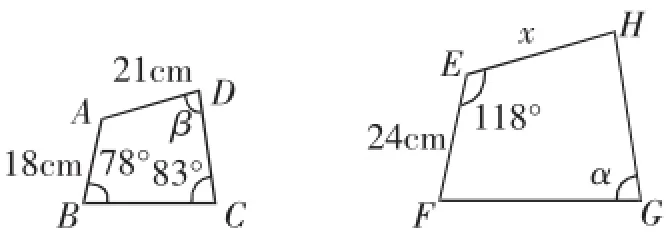
图1

练习

1.在比例尺为1∶10000000的地图上，量得甲、乙两地的距离是30cm，求两地的实际距离.

2.图2所示的两个三角形相似吗？为什么？

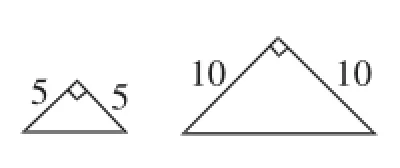
图2

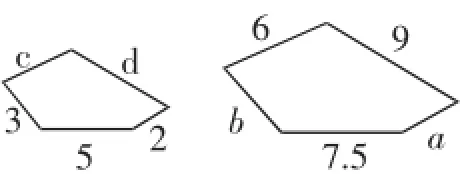
图3

3.图3所示的两个五边形相似，求a、b、c、d的值.

以上三个习题从整体上看都用到了相似比的知识，但是细看并不属于同类题.New Syllabus Mathematics中同样出现这三个习题，且都在相应的例题和解答后呈现，分别是例11、例5、例6，学生模仿习题即可解答.

（2）定理的探究过程.

中、新两本教科书对三角形相似的判定定理的探究方式，也存在很大的差异.《数学》引导学生根据全等三角形的判定定理类比探究相似三角形的判定定理.即由全等三角形的判定定理SSS得到相似的判定定理一：三边对应成比例的两个三角形相似；由SAS得到定理二：两边对应成比例且夹角相等的两个三角形相似；由AAS（ASA）得到定理三：两角分别相等的两个三角形相似. New Syllabus Mathematics则引导学生观察三组图形，根据相似图形的性质，分别思考对应边的比相等或者对应角相等的两个图形是否相似，从而得出结论：如果两个三角形的对应边的比相等或者对应角相等，那么这两个三角形相似；如果两个四边形或更多边形的对应边的比相等且对应角相等，那么这两个图形相似.

《数学》训练学生数学逻辑的严密性，重视合情推理和演绎推理，通过每一步严谨的证明得到定理.而New Syllabus Mathematics在发展学生思维方面则优势突出，重视学生思维的碰撞，通过观察、思考、交流、探究的方式得到定理.《数学》的这种训练也是造成中国学生在学习数学过程中容易形成思维定式的重要原因.因此，《数学》可以在保证逻辑正确的前提下，适当增加对学生数学思维的训练，开发学生的数学潜能，以全面提升其数学素养.

3.例题与习题的难度.

例、习题的难度可衡量出教科书编写者对学习者所要达到的要求［6］，笔者利用“数学课程的综合难度模型”［7］，对《数学》和New Syllabus Mathematics中的题目进行分析统计.本文选取教科书中所设置的探究、思考、例题、课堂练习进行对比.如表2所示，为两种教科书各难度因素的难度值统计.

表2 两种教科书题目难度因素对照

根据表2，做出两本教科书例题与习题难度因素的雷达图，如图4所示.由表2及图4直观看出：在推理和知识含量两个因素上，《数学》教科书难度高于New Syllabus Mathematics；在背景因素上，《数学》难度低于New Syllabus Mathematics；在探究和运算因素上，两本教科书的难度相当.探究、背景、运算、推理、知识含量5个因素对应的权重值分别为a1=0.210，a2=0.120，a3=0.185，a4=0.225，a5=0.26.得New Syllabus Mathematics的综合难于为2.14，《数学》的综合难度为2.26，即《数学》的综合难度大于New Syllabus Mathematics的综合难度.

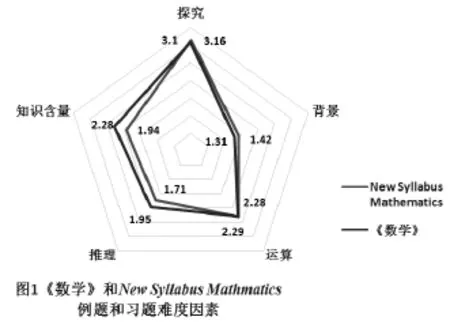
图4 《数学》和New Syllabus Mathematics例题和习题难度因素

新加坡数学题的难度并不高，但新加坡在数学教育方面取得的成就却受人瞩目.因此，注重基础知识的数学教育也可以取得较高的质量，学生对基础知识掌握扎实，会有更大的发展空间.“基础知识”和“基本技能”也是我国“四基”教育中重要的基础，在新课程改革的背景下，不仅要继承，更要发扬.

四、教科书对学生“能力培养”的比较

《标准》中指出“课程设计要满足学生未来生活、工作和学习的需要，使学生掌握必需的数学基础知识和基本技能，发展学生的空间想象能力、逻辑思维能力、运算求解能力、数据处理能力和综合应用能力”.在“相似”部分，主要涉及对学生逻辑推理能力和综合运用能力的培养，因此，本文通过对中、新教科书中所体现的“逻辑推理能力”和“综合应用能力”比较，得出结论，以期对我国数学教科书的编写产生积极的影响.

1.逻辑思维能力的发展.

学生在解决数学问题的过程中，思维能力［8］能得到逐步提高，以下从课本中的探究和例题出发，比较两本教科书对思维发展的重视程度.

（1）探究中所体现的思维.

《数学》和New Syllabus Mathematics中的探究主要是对“相似三角形的判定定理”的探究.《数学》重视合情推理和演绎推理，运用类比的方法，渗透数学思想，通过每一步严谨的证明得到定理，并且注重科学探究方法的掌握.New Syllabus Mathematics中主要是对“相似三角形”性质的探究，通过观察、思考、交流、探究的方式得到该定理，整个过程将自主探索、合作交流落到实处，培养学生灵活、发散的探究能力.

（2）例题中展现的思维.

《数学》和New Syllabus Mathematics中的例题均是在各个“探究结果”后出现，是对新定理的举例运用，及时巩固所学知识.不同的是，《数学》按照“题目”加“分析”加“解答过程”的模式.New Syllabus Mathematics中例题则是遵循“题目”加“知识点”加“解答过程”的模式.在这一方面，国内外教科书各有千秋，《数学》中的“分析”在展现解题思路的同时，也反映了题目的设计意图，帮助学生形成良好的思维逻辑.这与我国所提倡的三维目标中的“过程与方法”相适应，即学生的学习不仅是结果的学习，更是思维发展的过程.在这个过程中，学生体会数学的变化，感受学科的形成.New Syllabus Mathematics在例题的题头，分别明确写着哪个知识点，基本达到什么程度，这样有利于学生在大脑中搜索该方面的知识.

2.综合应用能力的培养.

《数学》对“相似”的应用主要有：相似三角形的判定、位似.New Syllabus Mathematics对“相似”的应用主要有以下几个方面：相似图形的判定、比例尺在地图中的应用、画扩大（或缩小）图，实际问题中高度的测量.《数学》和New Syllabus Mathematics都十分重视对学生应用能力的培养，重视学生问题解决能力的培养.但不同之处在于，《数学》重视逻辑推理和定理应用能力的培养，通过定理的探究和应用，加强学生的基础知识和基本技能.New Syllabus Mathematics则通过作图、实际应用等问题培养学生多方面的综合应用能力、动手实践能力，拓展学生的思维.

五、结论和启示

1.研究结论.

在内容方面，《数学》和New Syllabus Mathematics“相似图形”部分的侧重点不同，前者重“推理证明”，后者重“实际应用”，分别体现了两种不同价值取向.《数学》重视“相似三角形判定定理”的推导和证明，通过类比的方法推导判定定理并加以应用；同时，《数学》注重数学知识之间的联系，将“相似”与“坐标”结合起来得到“位似”，使知识得以升华.New Syllabus Mathematics则重视“相似的性质”的探索及其在实际中的应用，通过画扩大（或缩小）图训练学生的动手实践能力.New Syllabus Mathematics的例题与习题难度较《数学》偏低，该教科书更加注重基础知识的训练，不做偏题、怪题.

培养目标方面，两本教科书也存在较大的差异.《数学》注重培养学生严谨的逻辑推理能力；New Syllabus Mathematics更加重视培养学生灵活的探究能力和实际应用能力，发展学生的个性思维.

2.对我国教科书编写的启示.

（1）注重目标导引.

目标是指引学生学习的方向，明确的学习目标可以使学生抓住学习重点和难点，有的放矢.《数学》前言部分虽然通过问题将学生带入到新课的学习中，但是并没有明确指出学习目标.而New Syllabus Mathematics中的前言部分值得我们学习和借鉴，其设置在每章节最前面的目标导引，不仅可以在学生学习之前给予其明确的引导，同时，学生可以在学习完本章后对照目标，查漏补缺，进行归纳，这对于学生初学和复习梳理都是非常有帮助的.

（2）加强“四基”的训练.

新加坡的数学课程非常重视对基础知识的理解和对基本技能的运用.New Syllabus Mathematics的难度虽然比《数学》偏低，但新加坡学生在国际测试中一直表现优异，可以认为，这与他们扎实的基础是分不开的.New Syllabus Mathematics中每一道课堂习题都有例题作为先导，并且每道例题均有详细的解答过程，无难题、怪题，旨在夯实学生的基础，为培养更高层面的问题解决能力作好准备.《数学》的编排可以学习New Syllabus Mathematics的一些模式，以便更好地落实《标准》中的“四基”.

（3）培养学生的问题解决能力.

新加坡的数学将问题解决作为数学学习的核心，而《标准》也提到学生应当通过义务教育阶段的数学学习，“形成解决问题的一些基本策略，体验解决问题策略的多样性”.两本教科书在训练学生思维、发展学生问题解决能力上虽有所不同，却都非常重视.在教科书编写与教学实施过程中，不仅要强调知识与技能的训练，也要注重问题解决能力的培养.例如，加强“相似”知识与其他知识之间的对比与联系，可以帮助学生建构完善的知识体系，从而增强学生的问题解决能力.再如，充实习题的背景，增强习题与学生生活的联系，同样可以达到培养学生问题解决能力的目的.

（4）“推理”和“应用”相结合.

相对于《数学》重视培养学生严谨的思维和推理能力，New Syllabus Mathematics更加注重学生灵活的探究和应用能力.两本教科书各有千秋，可相互学习，相互借鉴.《数学》可以在不失推理的基础上增加更多实际应用，以增强学生的动手实践能力.例如，New Syllabus Mathematics中将利用相似性质画图作为本章的重点之一，将“比例”与现实的房子、地图结合起来，以锻炼学生的实践能力，这都是值得我们学习的地方，即注重数学的现实性.荷兰数学教育家弗赖登塔尔也曾提出“现实数学教育”，就是将数学学习与现实生活密切联系起来，把学到的数学知识应用到日常生活中去.加强数学与现实生活的联系，有利于引起学生对数学的兴趣，有利于学生了解数学的价值.

1.中华人民共和国教育部.义务教育数学课程标准（2011年版）［S］.北京：北京师范大学出版社，2011.

2.张晓贵.从新加坡数学课程五边形谈起［J］.数学教学通讯，2006（2）.

3.李海东.数学（九年级下册）［M］.北京：人民教育出版社，2012.

4.Dr Joseph Yeo，Teh Keng Seng，Loh Cheng Yee，Ivy Chow，Neo Chai Meng，Jacinth Liew.New Syllabus Mathematics2（7thEdition）［M］.Singapore：ShingleePublishers PteLtd，2013.

5.朱哲.新加坡数学教科书中的“勾股定理”［J］.数学教学，2008（4）.

6.徐芳.不同版本教科书的例习题比较研究——以人教A版和苏教版中“导数概念”为例［J］.中学数学（下），2016（10）.

7.鲍建生.中英两国初中几何数学课程综合难度的比较研究［D］.华东师范大学，2002.

8.唐恒钧，张维忠.中美初中几何教科书“相似”内容的比较［J］.数学教育学报，2005，14（4）.