“有理数的加法（1）”教学实录及立意阐释

☉江苏盐城市第四中学周中琴

“有理数的加法（1）”教学实录及立意阐释

☉江苏盐城市第四中学周中琴

近日，笔者有幸开设了“让学引思为学而教”研讨课，在课堂教学展示环节执教“有理数的加法（1）”，获得了评委的一致好评.本文呈现该课的教学实录，并对其教学立意进行阐释，不当之处，敬请指正.

一、教学实录

师：同学们，进入初中我们学习了负数，这样数的研究范围就扩充到了有理数，从而对小学阶段所熟知的一些内容就有必要作更进一步的认识.下面请同学们看大屏幕，思考下列两个问题：

（1）在小学阶段一个数是由其“绝对值”决定的，进入初中有什么变化？

（2）在小学阶段两个数的加法有几种情况？进入初中有什么变化？请举例说明.

（给学生2分钟的思考时间，然而找学生回答）

生1：第（1）个问题在上节课就讲过，进入初中一个数是由其“符号”和“绝对值”两部分构成的.

师：这位同学回答得不错，比如“-3”就是由其“符号（负号）”和“绝对值（3）”两部分构成的.下面请另外一位同学回答一下问题（2）.

生2：在小学阶段只有“正+正、正+0”；进入初中以后学习了负数，所以又有了“负+负、正+负、负+正、负+0”等几种情况.

师：回答得非常好，比如，对于“正+正”，老师举个例子“（+3）+（+2）=”，其他的几个你能分别举几个例子吗？

生2：（-3）+（-2）=、（+3）+（-2）=、（-3）+（+2）=、（+3）+

0=或（-3）+0=.

师：还有需要补充的吗？

生2：没了.

师：这位同学起来补充一下……

生3：老师，他忽略了一种特殊的情况，就是两个互为相反数的有理数的和，比如“（-3）+（+3）”这种情况.

师：这样经过同学补充我们就得到了六个算式……

在学生回答过程中，生成如下板书：

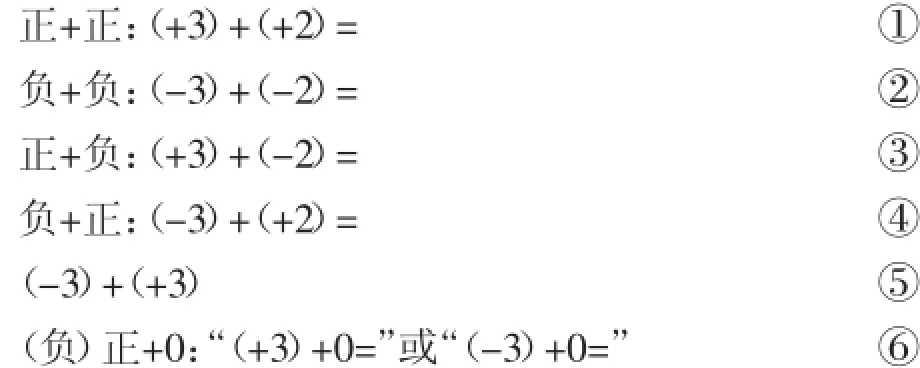
师：同学们，这就是我们这节课要学习的“有理数的加法（1）”（板书）.下面请同学们看大屏幕，读一下本节课的学习目标，在本节课结束时反思一下自己的目标完成情况.

出示本节课的学习目标：

（1）经历探索有理数加法法则的过程，理解有理数加法的意义及其法则，并能熟练地进行有理数加法运算；

（2）在问题解决过程中体验成功的乐趣，并体会相关数学思想和方法（分类讨论、数形结合）.

师：我们回过头来再看这6个算式，下面先给同学们2分钟的时间，尝试得到上述6个算式的结果.

（学生独立思考）

师：好，时间到.下面请同学们以小组为单位展开小组讨论，对上述6个算式的合理性进行解释.在讨论过程中重点思考下列两个问题：（1）结果是多少？（2）你是如何得到结果的？（提示：可以从多个角度进行解释）

师：请这个小组派代表回答一下.

生4：我们小组以“（-3）+（-2）=”为例进行说明，比如，我借了同桌3元钱，又借了同桌2元钱，最后借了同桌5元钱，所以（-3）+（-2）=-5.

师：这位同学回答得非常漂亮，他将生活中的“借钱”和数学中的“符号”进行了联系.其他小组还有不同说法吗？

生5：我们小组以“（+3）+（-2）=”为例进行说明，电梯在3层，下降2层，位于1层，所以（+3）+（-2）=+1.

生6：我们小组以“（-3）+（+2）=”为例进行说明，现在气温为零下3摄氏度，上升2摄氏度以后，是零下1摄氏度，所以（-3）+（+2）=-1.

师：可以看出，这三位同学分别以生活中的实例，对上述算式②③④进行了解释，回答得都非常好，体现了数学与生活的联系.下面，请同学们思考，我们能否利用刚刚学习的数轴对上述式子的合理性进行解释呢？比如，老师以第①个为例子进行说明，下面请同学们看大屏幕，认真听老师讲解：我们规定原点为起点，向右为正，向左为负，从而先以原点为起点向右“走”三个单位长度，箭头指向右方表示“+3”；在表示第二个数时要以第一个数的终点为起点，再向右“走”两个单位长度，箭头指向右方，从而最后的结果是以原点为起点，箭头指向右方（符号为“+”），长度为5的一个数，从而我们有（+3）+（+2）=+5.同学们看明白了吗？下面请同学模仿老师的做法，把其他几个算式在数轴上表示一下，表示完后请同学们思考下列两个问题：（1）结果的符号是如何确定的？（2）结果的绝对值是如何确定的？一会儿我找同学总结一下.

（学生独立思考）

师：时间到，同学们思考得怎么样呢？请这位同学回答一下.

生7：老师，我看出了互为相反数的两个数的和为0.

师：还有吗？

生8：同号的两个数相加，符号不变，绝对值是其绝对值的和.还有就是，任何一个数与0相加，还等于这个数本身.

师：还有吗？（众生摇头）下面请同学们以小组为单位讨论一下，看中间（指着板书）这一部分该如何总结.

生9：老师，异号的两个数相加，符号由绝对值大的数决定，绝对值是较大的绝对值减去较小的绝对值.

师：非常好，这样我们就得到了有理数的加法法则，请同学们看着大屏幕或课本默读两遍……

在同学们回答过程中形成下列板书：

1.法则：

（1）同号两数相加，取相同的符号，并把绝对值相加.

（2）绝对值不相等的异号两数相加，取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值.互为相反数的两个数相加为0.

（3）一个数同0相加仍得这个数.

师：同学们掌握得怎么样呢，下面看教材的例题：（按照法则按部就班进行）

师：可以看出有理数加法的运算步骤关键的有两步，一是确定符号，二是确定绝对值.

在讲解过程中生成下列板书：

2.例题：

限于篇幅，下略.

二、教学立意

1.一条主线：前后一致、逻辑连贯.

章建跃教授曾说：“在课堂教学中，要以知识的发生、发展过程和理解数学知识的心理过程为基本线索，为学生构建前后一致、逻辑连贯的学习过程，使他们在掌握数学知识的过程中学会思考.”因此本课例在设计过程中从数学内部的矛盾出发，引导学生得出本节课的主线——6个算式.在问题解决过程中，6个算式贯穿始终，前面承接了小学阶段学习的加法，后面引出了下节课要学习的内容——多个数的加法、减法、加减混合运算等（本课例在小结环节设计了问题：你觉得下节课要学习哪些内容）；同时，本课例在作业环节与开课之处做到了前后一致，设置了下列选做作业：同学们，通过本节课的学习，你是否对“加法”有了更深刻的认识？请写一篇反思性的小文章，谈谈你的认识.

2.两种思想：分类讨论、数形结合.

日本数学教育家米山国藏曾经说过：“学生们在学校所学的数学知识，在进入社会后，几乎没有什么机会应用，因而这种作为知识的数学，通常在出校门后，不到一两年就忘掉了.然而不管他们从事什么职业，那种铭刻于头脑中的数学精神、数学的思维方法、研究方法、推理方法和着眼点等，都随时发生作用，使他们受用终身.”上述论断中提到的“数学精神、数学的思维方法、研究方法、推理方法和着眼点等”正是“数学思想”的体现.有专家指出：数学思想只可意会，不可言传.但是，笔者却认为，一线教师应该在课堂教学中进行渗透，甚至需要“点破”，否则，等着学生去领悟可能会花费大量的时间，因此应该在课堂教学中让隐性知识显性化，比如，在本节课的小结环节，笔者着重引导学生总结在问题解决过程中用到的数学思想方法——分类讨论、承前启后，相信，经过老师一段时间的努力，必会实现在“授之以鱼”的基础上“授之以渔”.

3.三次打磨：终身难忘、刻骨铭心.

磨课是促进青年教师专业成长加速的有效手段.本课例前后经过了三次比较大的修改过程，在一次次打磨中笔者加深了对课标、教材的认识，深刻理解了教材的编写意图，实现了“教教材”向“用教材教”的积极转变.同时，在课例设计过程中，比较了不同版本教材中本节课的呈现方式，在“百花齐放”中实现了“一枝独秀”.

我们为上述课例所做的努力只是初步的，希望更多的一线教师参与进来，同时对课例提出更多修改意见.

1.章建跃.构建逻辑连贯的学习过程使学生学会思考［J］.数学通报，2013（6）.

2.刘东升.承前启后：一种“生长式”的课题小结——以李庾南老师的课例为例［J］.中学数学教学参考（中），2014（11）.

3.孙庆民，于彬.基于“导学反思”教学法的教学案例及思考——以“平行四边形的性质（第1课时）为例”［J］.中国数学教育（初中版），2016（6）.

4.于彬.前后照应：一种“点睛式”的课题结构［J］.中小学数学（初中版），2016（3）.