明晰尺规功能，让明理与得法同行

☉江苏如皋市实验初中冒劼

明晰尺规功能，让明理与得法同行

☉江苏如皋市实验初中冒劼

尺规作图是指用无刻度的直尺和圆规进行的作图，它是学生必备的一项基本技能.初中阶段，学生将要学习五种基本作图和一些基于基本作图的组合作图.为此，人教版教材自七年级上册第四章开始，以“作一条线段等于已知线段”这一基本作图为开端，将其他作图循序渐进地安排在整套教材之中.显然，无论是基本作图的编排，还是组合作图的设计，都经过编者精心安排.然而，通读全套教材，笔者并未发现对圆规和直尺这两件工具在作图中的功能介绍，对于这样的安排，不知教材编者是如何考虑的.这样的缺失，导致学生对尺规作图获得的结论仅“知其然”，而“不知其所以然”.为此，在人教版八年级上册全等三角形单元教学中，笔者明晰了尺规的功能，并让学生结合尺规功能分析作图过程，使得教学中的明理与得法同步.

一、“12.2三角形全等的判定（第1课时）”的三则教学片断

1.揭示尺规功能.

师（拿着圆规）：这是什么？

生（齐答）：圆规！

师：有什么用？

生（齐答）：画圆.

师请一名学生到前面板演作圆，并让其他学生取出自己的圆规在纸上画圆.

师：你是怎画的？

生1：先找一个点，把圆规的一只“脚”戳进去，将另一只“脚”绕着这个点转一圈.

师：不错！在圆规旋转的过程中，这两个“脚”之间的距离会发生变化吗？

生（齐答）：不会！

师：这个距离是圆中什么的长度？

生2：半径！

教师请学生作出圆的一条半径.

师：圆有多少条半径？

生（齐答）：无数条.

师（指着圆上的任意一点）：连接这个点到圆心是半径吗？

生（齐答）：是.

师（指到圆上的另外一个点）：这个点呢？生（齐答）：是.

师：这些点到圆心的距离都相等吗？

生3：相等！

师：根据这个发现，想要作出到一个点距离等于定长的点，可以怎么作？

生4：以定点为圆心，定长为半径作圆.

师：对，圆规就是用来作“到定点的距离等于定长的点”的工具，这在我们今后的作图中将会发挥巨大的作用.除了圆规，在尺规作图中，我们还会用到直尺，大家知道直尺的作用吗？

生5：度量和划线.

师：在尺规作图中，我们不能用直尺的度量功能，只能用直尺的画“直”线的功能.接下来，我们就用这两个工具开启今天的学习.

2.判定方法探究.

探究先任意画出一个△ABC，再画一个△A′B′C′，使A′B′=AB，B′C′=BC，A′C′=AC.把画好的△A′B′C′剪下来，放到△ABC上，它们全等吗？

学生活动：自主作图，并在小组中交流各自的作法及发现的结论.

3分钟后，教师组织学生进行全班交流，并展示了规范的作图过程，如图1：

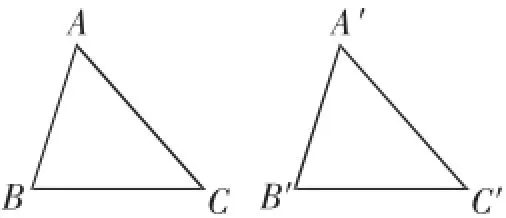
图1

（1）画B′C′=BC；

（2）分别以点B′、C′为圆心，线段AB、AC的长为半径画弧，两弧相交于点A′；

（3）连接A′B′、A′C′.

师：“以点B′、C′为圆心，线段AB、AC的长为半径画弧，两弧相交于点A′”，在这个过程中，你得到了哪些相等线段？

生6：A′B′=AB，A′C′=AC.

师：为什么？

生7：以AB、AC的长为半径，A′B′、A′C′是所作的弧的半径，所以这两组线段相等.

3.作一个角等于已知角.

已知：∠AOB.

求作：∠A′O′B′，使得∠A′O′B′=∠AOB.

学生活动：自主探究作法，并将自己的思路在小组中交流.

教师巡视指导，组织学生小组交流.

4分钟后，全班交流.教师先请学生展示作法，逐步调整学生的语言，最终形成规范的作图过程，如图2：

图2

（1）以点O为圆心，任意长为半径画弧，分别交OA、OB于点C、D；

（2）画一条射线O′A′，以点O′为圆心，OC长为半径画弧，交O′A′于点C′；

（3）以点C′为圆心，CD长为半径画弧，与（2）中所作的弧交于点D′；

（4）过点D′画射线O′B′.

师：请结合这里的作图过程说出∠A′O′B′=∠AOB的理由.

学生陈述作图中通过圆规和直尺构造出的相等线段：O′C′=O′D′=OC=OD，C′D′=CD，并给出∠A′O′B′=∠AOB的完整理由.

二、片断简析

本节课来自人教版八年级上册第十二章全等三角形，将学习全等三角形的第一种判定方法“边边边”.本节课的主要教学内容为“三边分别相等的两个三角形全等”这一基本事实.在这一定理获得及应用过程中，将会涉及两次尺规作图：一次是探究定理过程中的作图比对，还有一次是作已知角的角平分线.上面的三则片断，完整地展示了本节课与尺规作图相关的教学：片断1，教师引导学生梳理圆规和直尺在尺规作图中应该发挥的功能，为下一步作图和明晰原理作铺垫；片断2，是学生获取“边边边”定理的一个重要环节，基于作图的探究将会让学生的交流对话言之有物，有利于学生归纳结论，积累尺规作图经验；片断3，是初中阶段的第二种基本作图“作一个角等于已知角”的学习，这是对“边边边”定理的应用.

上述三则片断，有着明显的内在联系，片断1是片断2、3得以顺利展开的基础.片断1中，教者花费很大力气，带领学生将他们所熟知的圆规的功能进行了梳理，明确了在作图中所起的作用；对于直尺，绝大多数学生都知道可以用来度量和画线，教师从学生的说法中抽取出尺规作图适用的功能——画“直”的线.在接下来的两则片断中，问题的探究与师生的交流始终紧扣尺规功能展开.找寻“图中存在的相等线段”，让作图过程中圆规和直尺的功能得以凸显出来，让每一名学生对结论得出的合理性和作图方法的规范性都有了较为全面和深刻的认识.

三、几点思考

1.教学铺垫应根据实际需求呈现.

数学教学应建立在学生的最近发展区之上，在获取新知前，我们应该帮助学生梳理出本课必备的基础知识，为新知的顺利生成扫清障碍.所以，在实际教学中，对于一些离当下认知较远但本节课又要用到的数学知识，我们应该为学生创设较为合理的问题情境，使之顺着学生的认知需求顺利呈现.以本文中的片断1为例，尺规功能的交待对本节课的两个作图，特别是作图成果的合理性分析影响巨大.所以，教师主动展示学生熟悉的圆规和直尺，以唤醒他们在上一学段积累的丰富的应用经验，并努力从中筛选出尺规作图适用的功能，这一切就是为后续的学习作铺垫，这样的铺垫恰到好处地展示在学生新知探索之前，弥补了因过长时间的间隔导致的知识缺失，夯实了学生进一步探究交流的知识基础.

2.原理明晰应紧贴探究过程进行.

《义务教育数学课程标准（2011年版）》提出了“作图不仅要知法，还要明理”的要求.知法保证了作图技能的应用性，而明理则提升了“法”的理论高度.在教学中，我们最起码要让学生知晓作图形成的结果的合理性何在，这对“法”的网络化和综合应用都非常有利.为此，作图教学，我们会从“法”和“理”两个维度上引导学生展开追问，力求让得法与明理同步.在本文的案例中，教师结合学生给出的作图过程展开追问：在这个过程中，你得到了哪些相等线段？结论成立的理由成为作图教学最为重要的一部分.显然，这种基于学生自主探究之上的追问与交流，让学生的思维发展顺着自己探究中获得的知识和积累的经验进一步展开，其效果一定是非常好的.

3.教材补白应基于内容详解展开.

教材，一般指课本.笔者所在地区初中数学使用的是人教版教材.在这套人教版教材中，七年级上册第四章几何图初步“4.2直线、射线、线段”中，首次出现了尺规作图的定义——“在数学中，我们常限定用带刻度的直尺和圆规作图，这就是尺规作图”.在后面的教材中，先后给出了作一条线段等于已知线段、作一个角等于已知角等基本作图和一系列基于基本作图的综合作图，然而，始终没有给出圆规和直尺的功能.这样的内容缺失，使得学生在接下来的几何作图中，对教材给出的作法中所述的作弧与作直线及取交点的真正缘由不能清晰认知.为此，我们有必要对尺规功能进行补白，使之在学生需要用的时候适时出现，服务于学生的进一步学习.当然，发现这些存在的内容缺失主要依赖于课前对教材的详细解读，这需要教师坐下来，静下心认真仔细地剖析当下的教学内容和与之相关联的教材内容，对于那些缺失的内容，我们应进行精心设计，既要考虑补什么内容，还要考虑在何时补，怎样补.只有基于内容详解之上的教材补白，才能真正服务于教学，使课堂教学得以顺利、有效地推进.