例谈数形结合思想在数学解题中的应用
2017-03-10
例谈数形结合思想在数学解题中的应用
☉江苏省常熟中学 曹正清
数形结合思想指的是通过“以形助数”或“以数解形”(借助数的精确性来阐明形的某种属性)的方式,把抽象的数学语言与直观的图形语言联系起来思考,也就是将抽象思维与形象思维有机地结合起来分析,力求在代数与几何的交汇点处寻求解题思路,进而解决问题的一种数学思想.本文以举例的形式分类探索数形结合思想在解题中的应用.
一、数形结合思想在“函数的零点”中的应用
近年来高考对“函数的零点”内容的考查比较稳定,大都需要结合图像,数形结合地解决问题,因此我们有必要让学生发挥函数图像的作用,以形示数,数形结合,解决有关方程根的个数问题.
例1若关于x的不等式(2x-1)2<ax2的解集中的整数恰好有3个,则实数a取值范围是_______.
分析:对不等式(2x-1)2<ax2的理解:①化归为不等式,但需要讨论变量x和参数a的范围;②化归为基本函数,利用函数图像处理问题.下面利用数形结合,用基本函数图像研究解的个数.
方法1:设f(x)=(2x-1)2,g(x)=ax2.
当a=0时,y=g(x)表示x轴,舍去.
当a<0时,y=g(x)表示开口向下,对称轴为y轴的二次函数图像,舍去.
当a>0时,y=g(x)表示开口向上,对称轴为y轴的二次函数图像,由ax2>(2x-1)2,得g(x)>f(x),即恰有3个整数x值,使得g(x)的图像在f(x)图像的上方,

图1
方法2:研究不等式ax2>(2x-1)2.
当x=0时,不满足舍去;

图2
方法3:研究不等式ax2>(2x-1)2,
当x=0时,不满足舍去;

图3
方法4:研究不等式ax2>(2x-1)2,由题意可知,a>0.
当x=0时,不满足舍去;
对于几何法更要通过化归转化为基本函数,并利用函数图像解决问题.在方法1~4中,化归程度层层递进,化归得越彻底,得到的基本函数图像越容易,解答也就越简单.函数不断等价转化的过程,正是数学思维力的体现.

图4
二、数形结合思想在“不等式”中的应用
近年的高考强调考查不等式基础知识的同时也很注重数学能力的考查和数学思想方法的应用,其中数形结合思想方法的应用不可忽视.所以在不等式的教学或复习中要有意识注意数形结合思想方法的渗透.
例2设f(x)和g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)g(x)+f(x)g′(x)>0且g(-3)= 0,求不等式f(x)g(x)<0的解集.
解:根据以上特点,不妨构造F(x)=f(x)g(x),符合题意的函数F(x)=f(x)g(x)的图像(如图5所示),
由图直接观察出所求解集是(-∞,-3)∪(0,3).

图5
三、数形结合思想在“线性规划”中的应用
线性规划问题是在约束条件下求目标函数的最值问题,从图形上找思路恰好就体现了数形结合思想的应用.运用数形结合思想考查化归转化能力、逻辑思维能力,是函数教学中的一项重要内容.

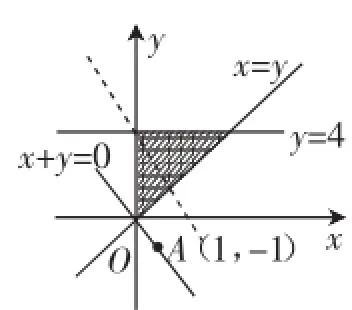
图6
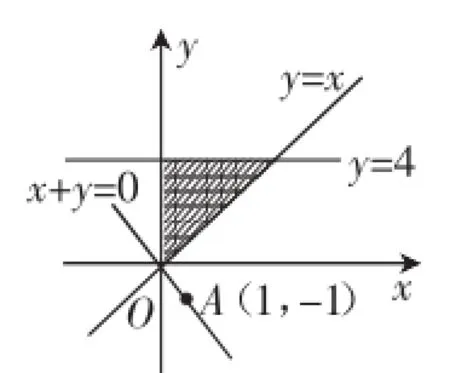
图7

图8
四、数形结合法在解三角形中的运用
例4设(fx)=sinxcosx-cos2(x+).
(1)求f(x)的单调区间;
(2)在锐角△ABC中,角A,B,C的对边分别为a,b,c,若f)=0,a=1,求△ABC面积的最大值.解:(1)略.(2)由题意,sinA=,a=1,A=,且△ABC的外接圆直径为a=2. sinA
如图9,取BC=1,其中A1C,A2B为外接圆直径,据题意顶点A在(不包括端点)上运动.
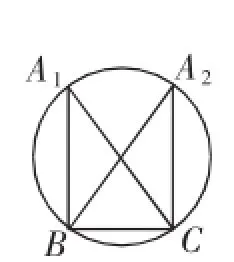
图9
本题的参考答案是根据余弦定理及基本不等式求出bc的最大值,最后利用面积公式求其最值,方法常规.但本题若选择采用以上图解法思考,会大大简化运算过程并且提高正确率.
五、数形结合思想在“点到直线的距离公式”中的应用
例5已知P是直线3x+4y+8=0上的动点,PA,PB是x2+y2-2x-2y+1=0的两条切线,A,B是切点,C是圆心,求四边形PACB面积的最小值.
本题直接求解较难,若能联想点到直线的距离公式,数形结合,以形助数,则更简洁.
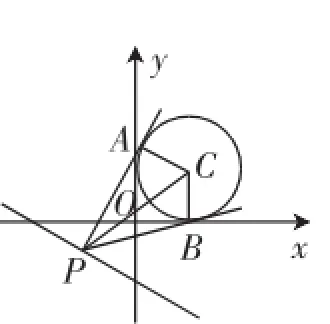
图10
六、数形结合思想在“解析几何”中的应用
例6已知点P在抛物线y2=4x上,那么点P到点Q(2,-1)的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为______.
解:点P到点Q(2,-1)的距离与点P到抛物线焦点的距离之和取得最小值时,点P到点Q(2,-1)的距离与点P到抛物线的准线的距离之和也取得最小值,这样就可以把点P到抛物线的焦点的距离转为到准线的距离求出.点Q(2,-1)在抛物线y2=4x的内部,要使点P到点Q(2,-1)的距离与点P到抛物线焦点的距离之和取得最小值,根据抛物线的定义知,须使点P到点Q(2,-1)的距离与点P到抛物线准线距离之和取得最小,即PQ⊥准线l时最小,如图11,则P.抛物线的定义是到焦点的距离等于到准线的距离,做题时常常用定义进行转化.
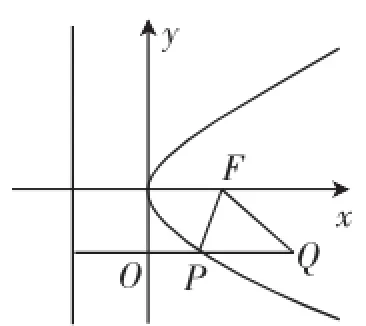
图11
七、数形结合思想在“三角函数”中的应用
在教材中利用单位圆的有向线段表示角的正弦线、余弦线、正切线,并利用三角函数线可作出对应三角函数的图像.如果能利用单位圆中的有向线段表示三角函数线,应用它解决三角不等式问题,简便易行.
例7解不等式|cosx|>|sinx|,x∈[0,2π].
从不等式的两边表达式我们可以看成两个函数y1= |cosx|,y2=|sinx|,在[0,2π]上作出它们的图像,得到四个不同的交点,横坐标分别为:,而当x在区间)内时,y=|cosx|的图1像都在y2=|sinx|的图像上方.所以可得到原不等式的解集为:

图12
八、数形结合思想在平面向量中的运用
平面向量,它具有“代数形式”和“几何形式”的双重身份,因此在解平面向量的相关题目的时候务必想到数形结合的方法,构造出符合题意的图形,具体问题具体分析.
例8已知点A,B,C在圆x2+y2=1上运动,且AB⊥BC.若点P的坐标为(2,0),则的最大值为_____.
解:如图13,因为点A,B,C在单位圆x2+y2=1上,AB⊥BC,所以AC是直径
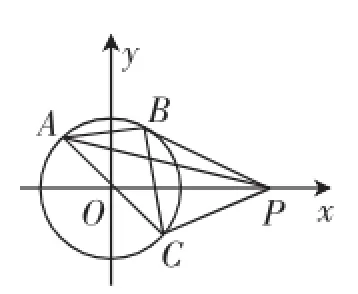
图13
本题以单位圆为载体,考查平面向量及最值的求解,构造出符合题意的图13是解决该题的关键.本题还可以用三角函数换元来做,但不如数形结合法来得轻松.
数形结合思想说到底就是要求学生体会不同知识之间的内在联系,加强对知识的综合运用,能够把所学的知识融会贯通,其目的不单单是追求解题技巧,而是更加关注学生对数学概念、数学本质的理解、数形结合思想的领悟,让学生的思维更加广阔,解题更加富有灵活性.这也是笔者写本文的目的.
