关注题型,积累方法
——以“平面向量问题”高考复习为例
2017-03-10
☉江苏省无锡市大桥实验中学 吴燕
关注题型,积累方法
——以“平面向量问题”高考复习为例
☉江苏省无锡市青山高级中学 俞飞
☉江苏省无锡市大桥实验中学 吴燕
高三直面高考,高考复习可谓临门一脚,必须拿捏到位,通过复习帮助学生熟悉高考中热点问题的常见题型及其解决方法.本文以“平面向量问题”的高考复习为例,就该话题进行分析.
一、关注高考热点
什么是热点问题?高中数学涉及的知识点很多,但是有些知识内容在各地高考卷和模拟卷中经常出现,则这一类问题属于高考热点问题.例如,近年来,高中数学的平面向量问题在高考卷以及各地高考模拟试卷中经常涉及,且其解题方法多种多样.平面向量兼具代数和几何特性,是沟通代数与几何的一种工具,是数学中数形结合思想的典型体现.笔者作为高中数学教学中的一线教师,对近年来各地区平面向量的高考题以及各地模拟题的类型进行了一些归纳整理.
二、注重题型整理与方法归纳
我们的整理要有明确的知识目标指向,在此基础上配以典型例题及其解析,通过对典例的分析总结出解决这一题型的数学思想方法.例如,“平面向量问题”进行了如下的题型划分.
1.运用平面向量数量积的几何意义
知识目标指向:向量数量积的几何意义是:a的模与b在a方向上的投影之积或者b的模与a在b方向上的投影之积.向量数量积实现了把不共线的两个向量积转化为共线的两个向量之积.《普通高中数学课程标准(实验)》中对该知识的要求是通过物理中“功”的实例,理解平面向量数量积的含义及其物理意义;体会向量数量积与向量投影的关系等.向量数量积既具有“形”的特征,又具有“数”的特征,是沟通三角、函数、空间、不等式等知识的桥梁.
例1设△ABC,P0是边AB上的一定点,满足P0B=AB,且对于AB上的任一点P,恒有则().
A.∠ABC=90°B.∠BAC=90°
C.AB=ACC.AC=BC
分析:这是2013年浙江省高考理科数学第7题.题目虽条件简单,却涉及动态变化的点,是一道具有平面几何背景关于平面向量数量积运算、不等式以及变量最值的综合问题.让众多学生不知所措,无法把握题目的要领所在.不少老师学生都采用坐标法,或基底法解决.下面,笔者用向量的几何意义解决.

图1
由数量积的几何意义可知,
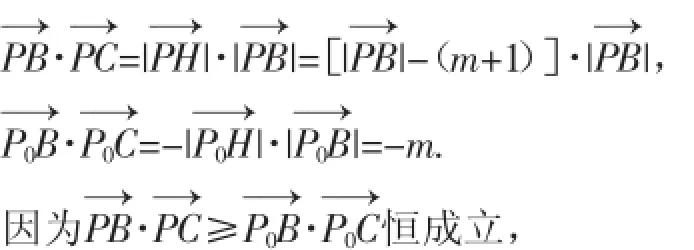
只需Δ=(m+1)2-4m=(m-1)2≤0即可,
即H是AB的中点.
所以△ABC是等腰三角形,AC=BC.
反思:从向量的几何意义着手、运用数形结合的思想方法,使得抽象的数学运算形式化、简单化、直观化,思路清晰明朗,有助于学生掌握和理解.但是鲜少会有学生从几何意义出发去解决有关向量数量积的相关问题.而事实上,掌握好向量数量积的几何意义对于理解向量数量积,解决其相关问题都有很大的帮助.
2.运用坐标法,将向量问题转化为函数问题
知识目标指向:在教学中经常提及的平面向量的解决方法是建系引入坐标,将向量的运算转化为代数运算,这样就可以将“形”与“数”紧密结合.建立直角坐标系是平面向量代数化的最直接的方法.
例2已知a,b是单位向量,a·b=0.若向量c满足|ca-b|=1,则|c|的取值范围是__________.
分析:由于a,b是相互垂直的单位向量,故可建立直角坐标系,运用向量的坐标运算来求解.
解析:由a,b是单位向量,a· b=0,故可设a=(1,0),b=(0,1),则a+b=(1,1),令=c=(x,y),得c-a-b=(x-1,y-1).又|c-a-b|= 1,所以有(x-1)2+(y-1)2=1,即点C在以(1,1)为圆心,以1为半径的圆上,如图2.
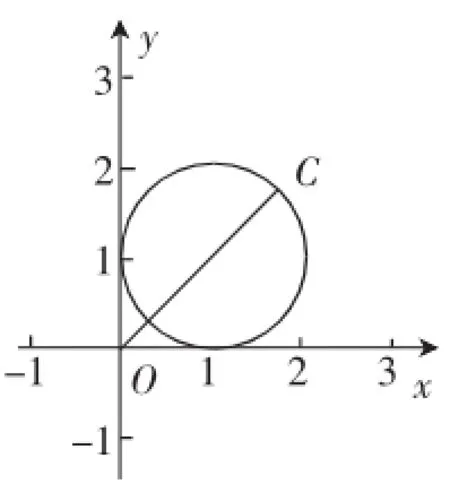
图2
3.运用平面向量几何特性解决问题
知识目标指向:很多向量问题无法建立坐标系,基向量法是个很好的选择,使用已知长度或者夹角的两个向量作为基底表示出需要的其他向量.下面举例说明.
例3在△ABC中,D是BC的中点,E,F是AD上的两个三等分点,的值是__________.
解法1(基底法):因为D为BC中点,E,F是AD上的两个三等分点,所以

同理
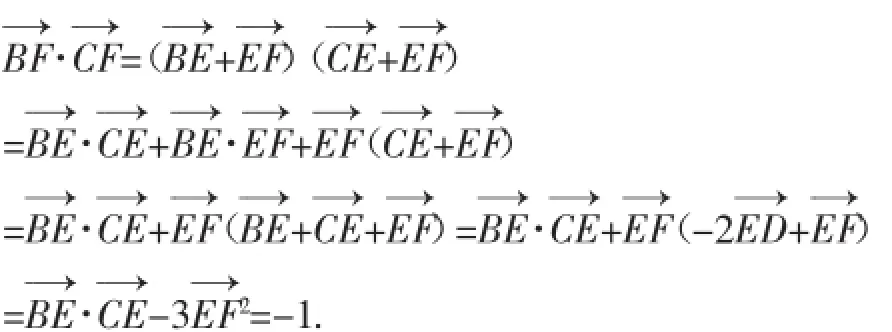
解法2(基底法):因为D为BC中点,E,F是AD上的两个三等分点,所以E为AF的中点,则

点评:解法2的本质仍然基底思想,通过向量的中点
基底法是平面向量的本质,是解决向量问题的通法,是培养思维能力的有效途径.
又D为BC中点,E,F是AD上的两个三等分点,
点评:极化恒等式是向量数量积的重要工具,应用十分广泛.本解法通过极化恒等式直接建立方程,简捷、快速,思维量小,大大减少了运算量.
由平行四边形的性质及余弦定理知,
(2AD)2+BC2=2(AB2+AC2)=2(BC2+2AB·ACcosA)= 2(BC2+8),即4AD2=BC2+16.(1)
又(2ED)2+BC2=2(EB2+EC2)=2(BC2+2EB·ECcosE),
点评:平面向量中的很多问题都有着其特定的几何背景,优美的几何意义,充分利用向量的几何模型,是解决向量问题的常用手段和重要策略.本解法正是通过利用平行四边形的性质、余弦定理建立方程,从而顺利解决问题.几何法解向量问题指向明确,可操作性强.
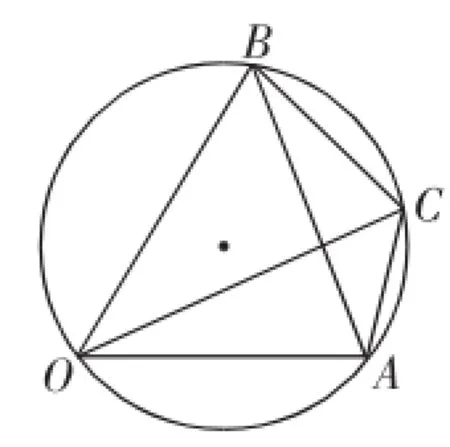
图3
4.通过构造图形解决
知识目标指向:向量加法、减法等运算特有的几何意义使得数形结合这一重要的数学思想在在解题中发挥着重要的作用.
分析:由本题条件可以考虑建系,用坐标运算解题,但变量较多,计算量相对较大.而按照题目要求直接构造图形,化繁为简.
三、结语
近几年的高考中,平面向量的题型越来越灵活、多变.应引导学生根据题中不同的条件选择相应的解题方法.本文仅仅例举了几种解决常见方法,意在教学中加强学生对解题工具的选择能力,加深学生对数学本质的理解.当然,除了“平面向量”这个考点,对于高中数学其他考点也是如此,我们要通过靠考前的复习帮助学生实现知识与方法的罗列,帮助学生提分增效.
