紧扣出发点拨动思维琴弦
2017-03-10冯桂群

【摘要】教学苏教版四下《多边形的内角和》时,教师可以让学生在操作、观察、猜想、验证、归纳等活动中发现数学规律,建构求多边形内角和的数学模型,感悟抽象、推理、建模等数学思想。教师可以引导学生将分割的起点由多边形的某个顶点平移到多边形内的某个点,再移到多边形边上的某个点,这有助于拓宽学生的思维,培养他们的创新意识,提升其数学核心素养。
【关键词】起点;分割;推想;建构;核心素养
【中图分类号】G623.5 【文献标志码】A 【文章编号】1005-6009(2017)01-0054-03
【作者简介】冯桂群,江苏省南通师范第一附属小学朝晖校区(江苏南通,226001)教师,高级教师,南通市数学学科带头人。
【课前慎思】
《多边形的内角和》是苏教版四下的内容,目的是让学生通过观察、操作、归纳、类比等活动,发现多边形内角和的计算方法。这节课是在学生认识了三角形内角和等于180°,了解了多边形基本特征的基础上教学的。教材重点是让学生用分割法将一个多边形分成几个三角形,把求多边形内角和的问题转化成求若干个三角形内角总和的问题,进而使学生发现多边形内角和与多边形边数之间的关系,获得计算多边形内角和的一般方法,从而使他们积累数学活动经验,感悟类比、归纳、数形结合、转化、建模等数学思想,初步形成问题意识、探索意识和创新意识。
在教学中,笔者发现,学生学习的难点在于如何巧妙地用最少的次数将一个多边形分割成若干个三角形。笔者这样解读学习难点的依据是四年级上册期末测试中的一道题:三角形的内角和是180°,五边形的内角和是多少度?笔者在批阅试卷时发现,部分学生算出五边形内角和大于正确值540°。经过调查,笔者了解到,学生不是不会将五边形分割成三角形,而是受之前画正五边形的对称轴和画长方形的对角线等作图活动的影响,将五边形分割成了3个以上三角形。其实,最简单的分割方法是从五边形的一个顶点出发,依次和与它不相邻的顶点连接起来,即分割2次得到3个三角形。因此,选择好分割的出发点并使分割次数最少是学生学习的难点,巧妙地利用学生已有的认知经验促进模型建构和实现适度拓展是教师教学的重点。笔者在多次试教与修改后,形成了以下较为流畅和深入的教学实践。
【课堂教学】
一、乐玩游戏,激趣生疑
师:孩子们,喜欢玩游戏吗?下面我们就来玩一个想象的游戏。请你们闭上眼睛,想象出两个点,两点之间只能画几条线段呢?
生:1条。
师:如果平均地对这条线段切一刀,线段会被分成几小段?
生:2段。
师:如果平均地对这条线段切2刀,会得到3段;平均地切3刀,就得到4段……如果将切成的3条线段首尾相接,围成的图形是三角形;4条线段首尾相接,围成的是四边形;5条线段首尾相接,围成的是五边形……
师:睁大眼睛仔细看,6条线段首尾相接,围成了六边形。请你想一想,至少要几条线段首尾相接才能围成封闭图形?
生:3条,围成三角形。
师:三角形的内角和是多少度?
生:是180°。
师:你想知道多边形的内角和怎样计算吗?今天我们就一起来研究“多边形的内角和”。(板书课题)
二、优化方法,探索规律
1.尝试解决,形成方法。
先从简单的四边形入手,引导学生进行探究。具体的做法是:为学生提供四边形纸片,让他们想办法求出四边形的内角和,并将思路标注在纸片上。然后让学生在四人小组里交流,并做好上台展示的准备。
2.小组合作,展示成果。
学生就上述问题进行汇报。
师:你们真能干,想到了好多方法。为什么有的同学用180°乘2来计算四边形的内角和?
生:因为四边形可以分成2个三角形,而三角形的内角和是180°。
师:把未知的问题转化为已知的问题,然后利用已知推想出未知。你们真厉害!
师:将四边形最少分割几次就分成了2个三角形?
生:一次。
師:这最少的一次不仅可以从图上看出来,还可以根据四边形的顶点个数推算出来。如果以四边形的某个顶点为出发顶点,只要向哪些顶点画分割线就行了?
生(做手势):相对顶点。
师:四边形的出发顶点有几个相对顶点?最少要分割几次?你能列式算出来吗?
生:4-3=1(次),这里的3是指出发顶点和它的2个相邻顶点。
师:看来,四边形不管以哪个顶点为出发顶点,每个出发顶点都只有1个相对顶点,所以最少要分割1次,算式是4-3=1(次)。而分得的三角形个数比分的次数多1,列式表示就是1+1=2(个)。所以四边形的内角和是180°×2=360°(如图1)。
三、发现规律,建立模型
1.研究五边形和六边形的内角和。
师:由此大胆地推算一下,五边形以某个点为出发顶点,它有几个相对顶点?最少分几次就能得到一些三角形?六边形呢?好,下面就请大家先独自分一分、算一算,再与同桌交流。
展示过程略。
小结:分割前要选好出发顶点,然后找它的相对顶点。有几个相对顶点,就要分割几次。分割得到三角形个数比分割次数多1。
反思:刚才通过画图与计算,我们成功地求出了四边形、五边形和六边形的内角和。难怪数学家华罗庚说:数缺形时少直观,形少数时难入微。数形结合百般好,隔离分家万事休。
2.研究其他多边形的内角和。
师:借助数形结合,你还想研究其他多边形的内角和吗?我们来分工合作,一、二大组研究七边形,三、四大组研究八边形。
生1(上台演示):我将七边形最少分4次得到了5个三角形(如图2),求七边形的内角和可以这样列式:7-3=4(次),4+1=5(个),180°×5=900°。
生2(上台演示):我将八边形最少分5次得到了6个三角形(如图3),八边形的内角和可以这样列式:8-3=5(次),5+1=6(个),180°×6=1080°。
3.列表、观察,发现多边形内角和的计算公式。
师:我们借助数形结合求出了好几个多边形的内角和,得出的数据中是不是隐藏着什么规律呢?为了便于观察和研究,我们可以通过列表来整理、研究数据。
学生报数据,教师填下表。
师:请大家观察列表,在4人小组里交流观察到的规律。
生:多边形的边数减3得到分割次数,分割得到三角形的个数比分割次数多1,所以分割得到三角形的个数可以用“边数-3+1”来算,“-3+1”连起来看就是“-2”。
师:分割的三角形的个数知道了,再乘180°,多边形的内角和就算出来了。所以,计算多边形的内角和的公式是什么?(板书:多边形的内角和=180°×(边数-2))
师:利用计算公式求多边形的内角和,感觉真方便。数学规律可以让复杂的问题迎刃而解,这就是数学的神奇魅力。
四、反思总结,灵活拓展
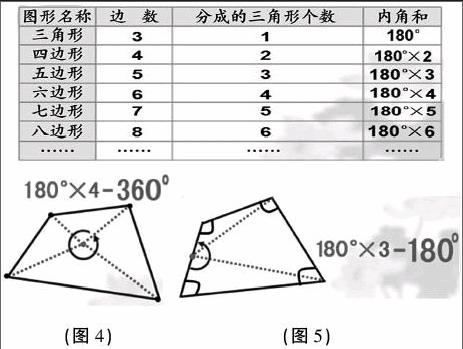
拓展1:根据乘法分配律,“多边形的内角和=180°×(边数-2)”还可以变形。即,多边形的内角和=180°×边数-360°。这一公式除了根据定律推算出来,还可以画出来。请同学们观看图4,如果将分割四边形的出发点由某个顶点移到图形内的任意一点,它有4个相对顶点,以它为出发点,可以将四边形分成4个三角形,4个三角形的内角和是4乘180°。显然,这4个三角形的内角和比四边形的内角和多中间的4个角,一共是360°,所以要求四边形的内角和就要再减去360°。
拓展2:除了从顶点或图形内的某一点出发,还可以从边上的某一点出发,向和它相对的顶点作分割线,会得到3个三角形(如图5)。这3个三角形的内角和比四边形的内角和要多,多的角就是边上的180°,所以用180°×3-180°=360°。回顾以上3种分割方法,可见,数学学习不仅要追求一题多解,更要讲究算法的优化。
【教后反思】
1.紧扣分割多边形的出发点,让学生将分割图的直观经验提升到理性高度。
借助研究三角形内角和、画图形的对角线或对称轴的学习经验,学生自然想到了用量、分、撕等方法来求四边形的内角和。在算法的对比求优中,笔者借助出发顶点、相邻顶点和相对顶点三者之间的位置关系,让学生明白了四边形中的某个顶点只有一个相对顶点,所以将四边形分割成三角形,最少只要分割一次,巧妙避開了画2条对角线来分割四边形的情况,并为后面的思维拓宽与深化埋下了伏笔。
2.紧扣分割多边形的结果,让学生在列表和观察中建构数学模型。
借助“从某一个顶点出发,用最少的次数将多边形分成几个三角形”这一问题,笔者不仅将复杂的数学问题转化为学生已经掌握的求几个三角形内角总和的问题,渗透了转化、数形结合的数学思想,更主要的是引导学生从数据中发现数学规律,建构起相应的数学模型,感悟到抽象、推理、建模等数学思想。
3.紧扣出发点的位置变化,让学生在思维拓展中感受数学思维的灵活多变。
英国教育家怀特海说:“教育需要解决的问题就是使学生通过树木看见森林。”引导学生将分割的起点由多边形的某个顶点平移到多边形内的某个点,再到多边形边上的某个点,不仅综合运用了平移、乘法分配律、画图等已有知识,还巧妙地拓展了学生的思维,培养了他们的创新意识,为学生进入初中后深入地研究多边形的内角和埋下了活思、活学、活用的种子,真正提升了他们的数学核心素养。<\\Ysc02\d\邱\江苏教育\小学版\2017\01\KT1.TIF>
