正矢波激励下简支印制电路板的跌落响应研究

陈思佳， 许富华,2， 阮 丽， 卢富德， 高 德

(1.浙江大学 宁波理工学院,宁波 315100; 2.太原科技大学 机械工程学院,太原 030024)

正矢波激励下简支印制电路板的跌落响应研究

陈思佳1， 许富华1,2， 阮 丽1， 卢富德1， 高 德1

(1.浙江大学 宁波理工学院,宁波 315100; 2.太原科技大学 机械工程学院,太原 030024)

对印刷电路板(PCB)的跌落响应进行了研究，将一对边固定一对边自由的电路板简化为简支梁，建立了其在正矢波脉冲激励下的动力学模型。利用SY11-100气压驱动垂直冲击试验台搭建跌落试验，测得电路板跌落时的脉冲激励以及电路板中心位置的加速度响应，通过与试验结果的对比验证所建动力学模型的正确性。在此基础上，对正矢波脉冲激励的周期以及PCB的材料结构属性对跌落冲击产生的最大应力的影响进行了分析。计算结果表明,电路板跌落冲击产生的最大应力以及达到最大应力所需的时间都与正矢波脉冲激励周期成正比，与材料结构参数λ成反比。

印制电路板；正矢脉冲；跌落冲击；动力学建模

随着电子工业的迅速发展,电子设备应用的范围越来越广,无论是在日常生活中还是在军事领域里,到处都可以看到电子设备的身影。电子设备在运输、贮存和使用过程中不可避免的会受到各种机械伤害：振动、冲击、离心力及运动产生的摩擦力等，其中又以振动与冲击对电子设备的伤害最大。而印制电路板是电子设备的重要组成部分,电子设备的大部分缺陷都来源于印制电路板,印制电路板的可靠性对电子设备至关重要。因此,为了保证印制电路板的可靠性,有必要在印制电路板的结构设计中进行全面的动力学分析。

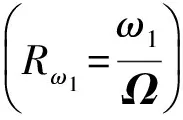
上述文献从多个方面对印制电路板的可靠性进行了研究，然而却鲜有人考虑在跌落过程中，电路板受到近似于正矢脉冲激励时，板的中心位置所受到的最大加速度(即脆值问题)以及最大应力。本文将对一对边夹持、一对边自由的印制电路板进行研究，根据边界条件建立其在正矢脉冲激励下的动力学模型，分析跌落冲击时电路板的加速度和最大应力随正矢脉冲激励变化的规律，并用跌落试验验证所建动力学模型的正确性，其结果将为电子产品的包装与防护提供理论指导和参考。

1 板级跌落冲击动力学建模

图1是包装运输过程中典型的板级跌落冲击示意图。它包括质量主体和电路板，电路板通过简支方式安装在质量主体上，构成整个电子产品，然后将其整体放在聚乙烯缓冲泡沫上，构成了电子产品的包装系统。由于电路板的质量远小于主体质量，产品自由跌落并压缩泡沫的过程中电路板对质量主体的影响可以忽略。

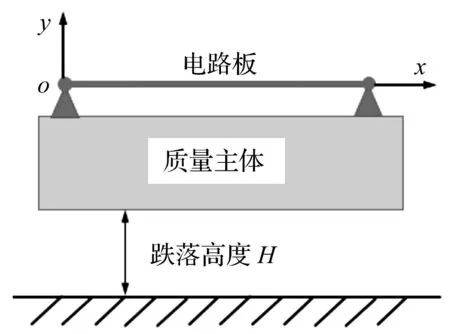
图1 电路板跌落示意图Fig.1 Schematic diagram of PCB drop impact

通常，物体在跌落至地面时会受到脉冲激励，由于物体的弹性可将其简化为一个半正弦脉冲激励Y=A0sin (Ωt) (0≤t≤T)。然而有学者研究发现，当有聚乙烯泡沫作为缓冲包装材料时，物体会受到近似于正矢波的脉冲激励Y=A0sin2(Ωt) (0≤t≤T)(详见文献[4]中图4)。由图2中可知，二者虽然幅值一样，但是半正弦脉冲是一个凸函数，其起始斜率很大；而正矢波脉冲的起始斜率很小，变化较缓。本文将对PCB在受到正矢脉冲激励时的脆值问题进行研究。

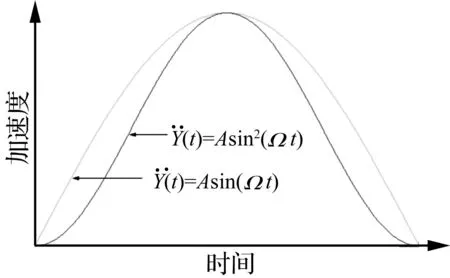
图2 两种激励模型的对比图Fig.2 Comparison of half-sine and versine incentive

假设质量主体是刚体，则板级跌落的冲击动力学行为可简化为印制电路板在边界支撑下承受一个加速度脉冲作用的动力学模型。对于印制电路板的边界条件，取较为常见的固定形式，即：一对边夹持，一对边自由。

对于一对边夹持、一对边自由的印制电路板可将其简化为简支梁梁模型。令梁身有效长度为L，其受力及变形模型如图3所示。

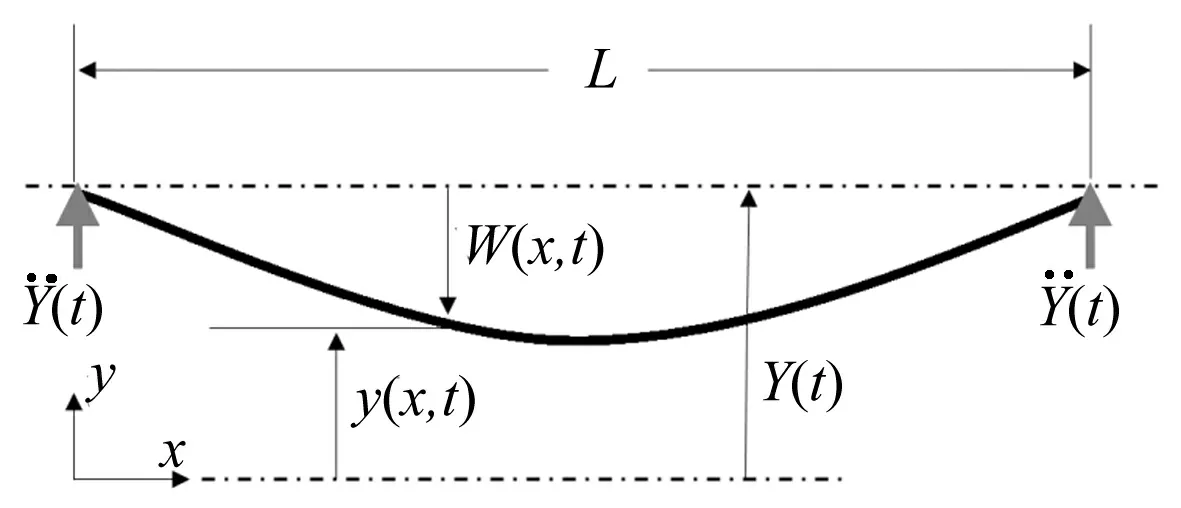
图3 两边简支的电路板模型Fig.3 Beam model of PCB

由图3可知,梁上任一点在竖直方向上的位移y(x,t)与脉冲Y(t)以及梁自身的挠度w(x,t)之间满足以下关系

y(x,t)=Y(t)+w(x,t)

(1)

在不考虑简支电路板对质量主体的动力学影响下，对图2进行动力学分析，得到[15-16]

(2)

式中：E为弹性模量;I为截面惯性矩;r为电路板密度;A为电路板横截面积。

将式(1)代入式(2)得

(3)

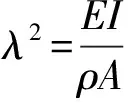
设正矢脉冲的函数表达式为

(4)

式中:A0为正矢波脉冲幅值;Ω为脉冲频率;T为脉冲周期。

简支梁的边界条件为：w(0)=w(L)=0

由上可知方程转化为求解挠度w(x,t)在Y(t)作用下的强迫振动。运用振型叠加法，假设梁的挠度为

(5)

式中:Wn(x)为梁的振型函数;qn(t)为梁的模态坐标;n为模态数。

对于简支梁，其振型为

(6)

将式(4)、式(5)、式(6)代入式(3)可得

(7)

于是,

(8)

所以，电路板的挠度可表示为

(9)

其中,

(10)

式中,ωn为易损件电路板的第n阶频率。

于是，电路板在跌落冲击时的加速度响应可表示为

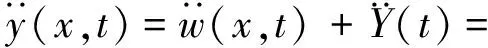
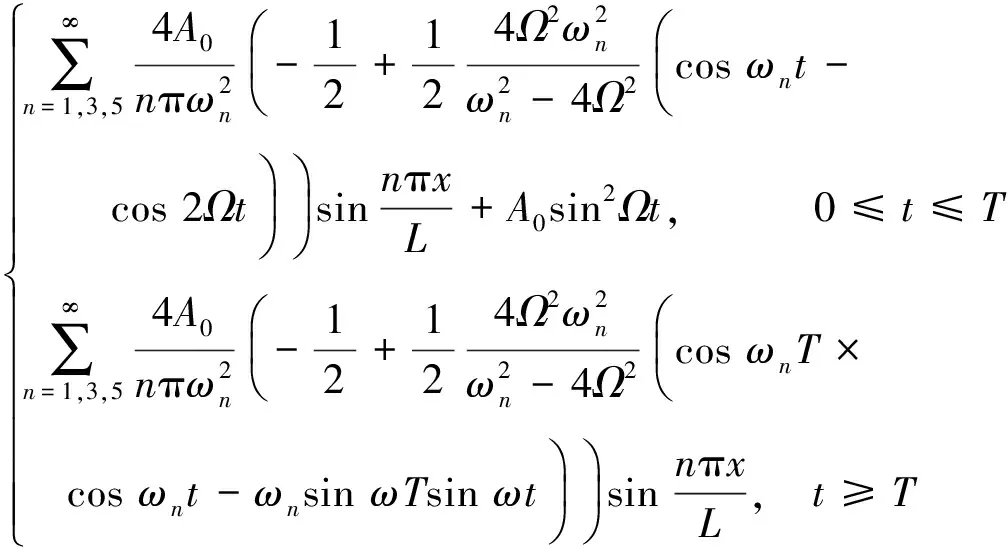
(11)

电路板几何中心处的应力为

(12)

为了能够直观地认识正矢脉冲激励与电路板的加速度响应之间的关系，根据式(11)可以得到正矢脉冲激励与其产生的电路板的加速度响应大致形态如图4所示。

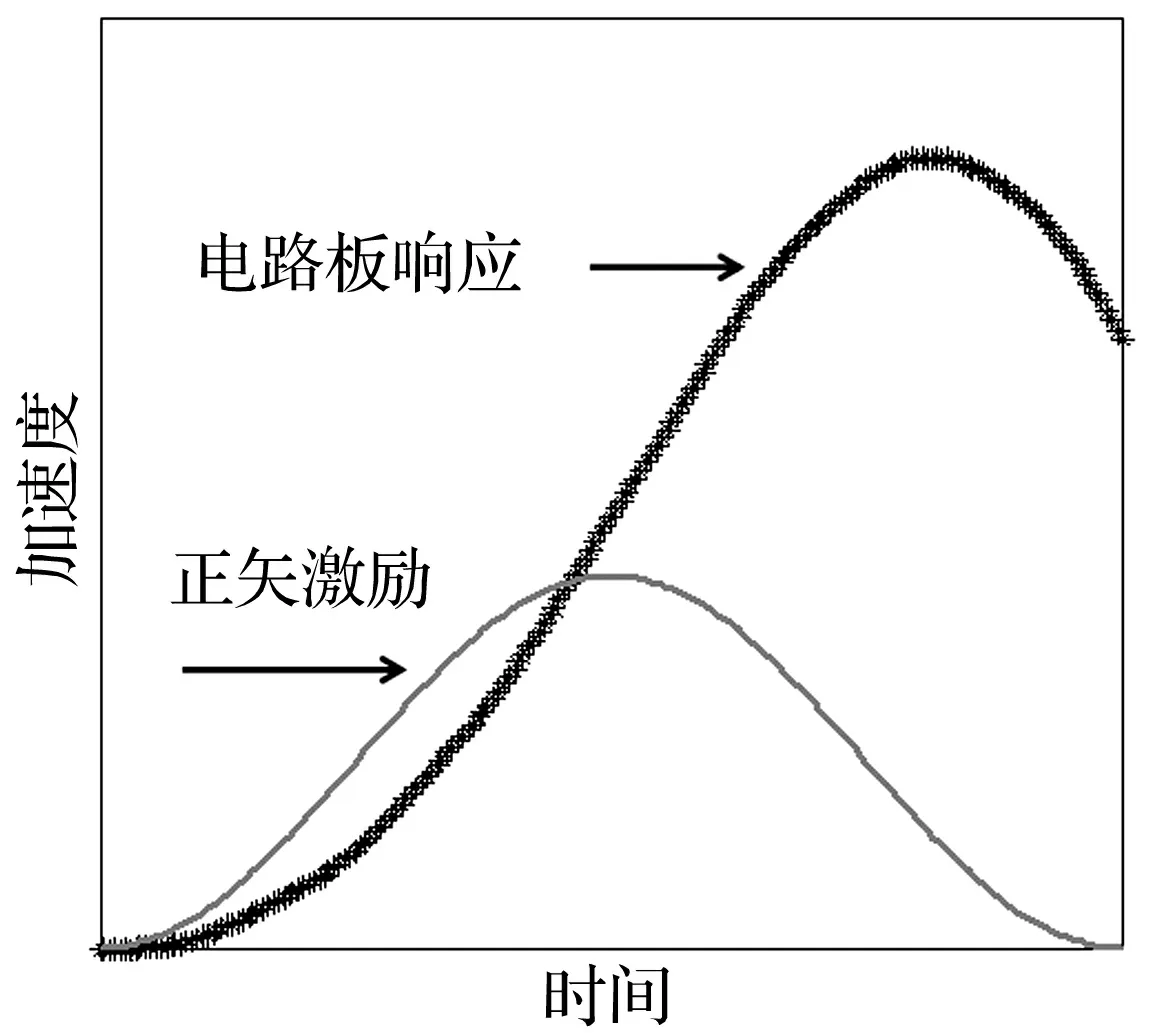
图4 正矢波激励及板的加速度响应曲线Fig.4 The curve of versine incentive and respond of PCB

2 跌落冲击试验

为了验证上述理论的正确性，本文使用SY11-100气压驱动垂直冲击、碰撞试验台搭建实验，如图5所示。其试验原理为：将试件通过夹具紧固到台面上，将工作台提高到一定高度，释放后自由跌落，台面底部与底座上的缓冲垫层碰撞，使台面受到一个向上的冲击载荷，再由台面将所产生的脉冲载荷传递给固定于台面的试件，从而实现对固定于台面上试件的冲击。

①-基座; ②-脉冲发生器; ③-跌落台; ④-导轨;⑤-夹具; ⑥-电路板; ⑦-加速度传感器图5 电路板跌落冲击实验系统Fig.5 The experiment system of PCB drop impact

本实验选用SY11-100自带的正矢脉冲衬垫，取试验对象PCB几何尺寸为0.3 m×0.2 m×0.002 2 m，并在电路板的几何中心和台面上分别安装加速度传感器。为了确保实验结果的准确性，本文用CMT6103型微机控制电子万能试验机测得PCB试件的弹性模量，并取平均值为21.54 GPa(见表1)。

表1 PCB弹性模量测试结果

由于跌落时所受的冲击激励为正矢波激励，由理论及实验数据都可得知电路板的加速度响应会在第一个波峰处达到最大值，之后由于没有激励的输入，电路板的加速度会逐渐衰减并最终趋于0。在包装应用力学中，对于产品的可靠性分析主要考虑产品的脆值，即产品的最大加速度值是否超过其许用加速度值。从式(11)容易看出PCB的最大加速度容易出现在几何中心位置，故只需对板的几何中心的加速度响应进行分析。

为了试验的科学性，取实验跌落高度分别为50 mm、100 mm和200 mm，测试这三种不同高度下PCB板的加速度响应。从图6可以发现，在这三种不同跌落高度下试验台面所受的脉冲激励均为正矢函数波形。经计算，这三种跌落高度所对应的正矢波脉冲的周期和幅值分别对应为0.02 s、0.019 s 、0.017 s和20 g、27 g、39 g。将上述参数和激励分别代入式(11)便可以得到电路板在不同跌落高度下加速度响应的解析值。通过图7对比发现，试验曲线与理论计算得到的解析值基本吻合。理论值的加速度曲线与试验数据中曲线的变化趋势一致，由于试件上加速度传感器以及材料非线性阻尼的影响，实验数据在误差允许范围之内。这就基本可以说明文中所建电路板的动力学模型的正确性。

(a) H=50 mm (b) H=100 mm (c) H=200 mm图6 不同高度下的冲击脉冲Fig.6 Pulse under different height

(a) T=0.02 s, A=20 g (b) T=0.019 s, A=27 g (c) T=0.017 s, A=39 g图7 实验数据与理论对比图Fig.7 The contrast diagram of experimental data and theoretical data

3 最大应力的影响因素分析

当电子产品受到跌落冲击时，其上受到的最大应力会受到各种因素的影响，如：电路板本身的材料和结构特性以及脉冲激励的幅值与周期。由式(12)可知,电路板的应力与脉冲的幅值成正比。本节将重点讨论在同一脉冲幅值下，不同脉冲周期以及不同材料结构参数λ对电路板最大应力的影响。

3.1 脉冲周期的影响

取脉冲幅值A0=20 g，PCB的密度为2×103kg/m3, 弹性模量为24 GPa，几何尺寸为0.3 m×0.2 m×0.002 m。分别取Ω=1/T为30π、40π、50π、60π和70π，Ω越大脉冲周期越短。

图8为不同正矢激励周期下电路板几何中心应力变化曲线。由图可知：随着脉冲激励周期的变短，电路板达到最大应力所需时间缩短，电路板的最大应力也同时变小。

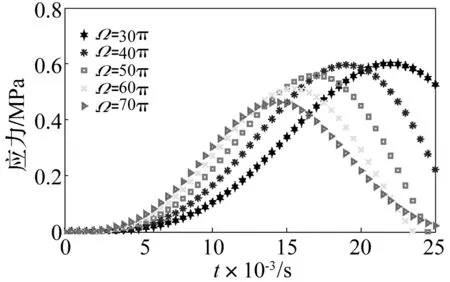
图8 正矢激励周期对电路板中心处应力的影响Fig.8 The effects of different period on the stress of PCB

3.2 材料的影响

取正矢波脉冲激励A0=20 g，T=0.02 s。PCB电路板密度为2×103kg/m3, 弹性模量为24 GPa，几何尺寸为0.3 m×0.2 m×0.002 m。令材料结构参数λ分别为0.5、0.8、1、1.5和2。图9为不同λ下电路板几何中心应力的变化曲线。从图中可以得出,随着材料系数λ的变大，电路板达到最大应力所需时间缩短，电路板的最大应力也同时变小。

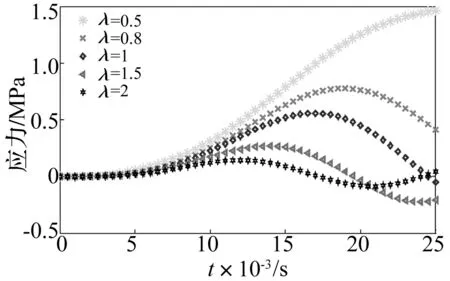
图9 不同λ对电路板中心处应力的影响Fig.9 The effects of different constant λ on the stress of PCB

4 结 论

本文对一对边夹持一对边自由的印制电路板在正矢脉冲激励下的动力学模型进行了研究。将电路板简化为两边简支的梁模型，跌落冲击过程处理为正矢脉冲激励下的受迫振动，并通过实验验证了所建动力学模型的正确性。通过研究发现：电路板跌落产生的最大应力以及达到最大应力所需的时间与正矢脉冲的周期成正比，与材料结构参数λ成反比。本文的研究结果将为印制电路板在跌落冲击作用下的可靠性与防护提供理论基础和一定的参考价值。

[ 1 ] TEE T Y，NG H S, PAN S. Board level solder joint reliability modeling of TFBGA package[C]//Tokyo Proceedings of ICEP Conference,2002:491-497.

[ 2 ] DARVEAUX R. Effect of simulation methodology on solder joint crack growth correlation[C]//Las Vegas:Proceedings of 50th Electronic Components and Technology Conference, 2000:1048-1058.

[ 3 ] TEE T Y, SIVAKUMAR K, DO-BENTO-VIEIRA A. Board level solder joint reliability modeling of TFBGA package[C]//Hong Kong:Proceedings of 2nd EMAP Conference,2000:51-54.

[ 4 ] 高德，卢富德. 聚乙烯缓冲材料多自由度跌落包装系统优化设计[J]. 振动与冲击,2012,31(3):69-72. GAO De, LU Fude. Optimization design of MDOF package cushioning system made of polyethylene[J].Journal of Vibration and Shock,2015,31(3):69-72.

[ 5 ] 张炜，薛飞，卢富德,等. 考虑易损件物品-EPE缓冲系统冲击响应分析[J].振动与冲击, 2015,34(9)：116-119. ZHANG Wei, XUE Fei, LU Fude, et al. Impact-response analysis of the system composed of critical component and EPE cushion[J].Journal of Vibration and Shock,2015,34(9):116-119.

[ 6 ] PITARRESI J M, GENG P, BLTMAN W,et al. Dynamic modeling and measurement of personal computer motherboard[C]//San Diego:IEEE Electronic Component and Technology Conference,2002: 597-603.

[ 7 ] TEE T Y，NG H S，LIM C T,et al. Drop test and impact life prediction model for QFN packages[J]. Journal SMT, 2003,3(16):31-39.

[ 8 ] WONG E H. Dynamic of board-level drop impact[J]. Transactions of the ASME, Journal of Electronic Packaging, 2004,127(3):200-207.

[ 9 ] WONG E H, MAI Y W, SEAH S K W. Board level drop impact-fundamental and parametric analysis[J]. Transactions of the ASME, Journal of Electronic Packaging, 2005,127(4):496-502.

[10] SUHIR E. Could shock tests adequately mimic drop test conditions[J]. Transactions of the ASME, Journal of Electronic Packaging, 2002, 124:170-177.

[11] TSAI T Y,YEH C L,LAI Y S.Response spectra analysis for undamped structural systems subjected to half-sine impact acceleration pulses[J]. Microelectronics Reliability, 2007,47(8): 1239-1245.

[12] 张波,丁汉,盛鑫军. 板级电子封装在跌落冲击载荷下的动态响应分析[J].振动与冲击,2008，27(6)：108-113. ZHANG Bo, DING Han, SHENG Xinjun. Dynamic response of a board level electronic package under drop impact load[J]. Journal of Vibration and Shock, 2008,27(6)：108-113.

[13] 刘芳,孟光. 电路板组件板级跌落冲击动力学分析[J]. 机械强度，2007,29(5)：713-716. LIU Fang, MENG Guang. Dynamic analysis of printed circuit board assembly subjected to drop impact [J]. Journal of Mechanical Strength, 2007,29(5)：713-716.

[14] 杨雪霞,肖革胜,树学峰. 板级跌落冲击载荷下无铅焊点形状对BAG封装可靠性的影响[J].振动与冲击，2013，32(1):104-107. YANG Xuexia, XIAO Gesheng, SHU Xuefeng. Effect of solder joint shape on reliability of BGA packages under board level drop test[J]. Journal of Vibration and Shock，2013，32(1):104-107.

[15] SINGIRESU S R.机械振动[M].北京：清华大学出版社,2009.

[16] 李惠彬. 振动理论与工程应用[M]. 北京：北京理工大学出版社，2006.

Dropping response of simple supported PCB under versine stimulation

CHENSijia1,XUFuhua1,2,RUANLi1,LUFude1,GAODe1

(1. Ningbo Institute of Technology,Zhejiang University, Ningbo 315100, China; 2.School of Mechanical Engineering Taiyuan University of Science and Technology, Taiyuan 030024, China)

Dropping impact response of PCB is studied in this work. The PCB is simplified as a simple supported beam and the dynamic model of the PCB under versine stimulation was also proposed. To validate the dynamic model, a dropping experiment was performed by SY11-100 vertical impact testing station. The pulse excitation and the acceleration response of the PCB were measured to compare with the result of the theoretical calculation. It is found that the period of the versine pulse stimulation and the material of the PCB have great influences on the dynamic response of the PCB. The results show that: the time to reach the maximum stress and the maximum stress of the PCB are both reduced as the period of the versine pulse becomes short and the material structure factorλincreases.

printed circuit board; versine pulse; dropping impact; dynamic modeling

国家自然科学基金(11402232;11302192)

2016-01-13 修改稿收到日期：2016-05-25

陈思佳 男，博士，讲师，1985年3月生

高德 男，硕士，教授，1963年6月生

TB485.3;O322

A

10.13465/j.cnki.jvs.2017.04.032