地铁列车运行引起远场低频振动响应预测研究

孙晓静, 袁 扬, 马 蒙, 刘维宁

(1.北京交通大学 土木建筑工程学院，北京 100044；2.天津市城市规划设计研究院，天津 300201)

地铁列车运行引起远场低频振动响应预测研究

孙晓静1, 袁 扬2, 马 蒙1, 刘维宁1

(1.北京交通大学 土木建筑工程学院，北京 100044；2.天津市城市规划设计研究院，天津 300201)

精密仪器对工作环境的振动要求通常有微振、低频等特点，因此准确预测分析列车振动对精密仪器的影响具有一定的难度。结合北京地铁16号线规划通过北京大学西门的工程案例，首次在频域内采用两位校准法进行了远场低频微振动的定量预测研究。研究过程中，利用实测钢轨振动加速度时程计算得到模拟地铁列车荷载；建立北京地铁4号线校准模型，利用实测隧道壁和地表的振动响应对输入荷载、模型参数选择进行校核，确保了模型的预测精度；最后采用校核过的建模方法建立地铁16号线预测模型进行低频振动预测。结果表明：利用该方法得到的地铁列车振动荷载及振动预测模型可以较准确的进行远场低频振动响应预测；地铁16号线地铁采用钢弹簧浮置板后，北大新建实验楼外预测点10～20 Hz频段的振动满足仪器振动要求，但10 Hz以下频段的振动仅满足VC-C标准，需进行实验室或仪器隔振处理。

低频振动；远场振动；两位校准法；动力有限元；列车荷载

近年来，国内各大城市的地铁新线建设如火如荼。在地铁线路开通运行前，对拟建线路环境振动影响预测的准确性将直接影响到减隔振措施的合理选择，也将影响到线路开通运营后沿线敏感目标是否会受到振动影响。常见的地铁振动预测方法有经验法、数值法和混合法等。国内外规范中分别给出了相应的经验预测公式和参数修正方法[1,2]，王另的等[3]在文献[2]基础上提出了一个适用于北京地铁环境振动的预测模型。常见的地铁列车振动预测数值方法包括有限元法[4]、有限元-边界元耦合法[5]、2.5维有限元-无限元耦合法[6]、薄片有限元-无限元耦合法[7]等，并广泛用于各类预测研究。

精密仪器是对环境振动最为敏感的一类受振体，其振动评价通常要考虑微振、低频等特点，预测难度也最大。既有研究精密仪器预测的案例[8-10]大多直接采用数值方法预测，振源与实验楼之间水平距离通常小于100 m。本文结合北京地铁16号线规划通过北京大学西门的工程案例，针对拟建线路与高精密实验楼间水平距离约200 m的远场微振动预测问题，首次在频域内采用两位校准法进行低频微振动的定量预测研究。

1 研究背景及方法

1.1 工程背景

北京地铁16号线西苑—海淀桥区间段规划从北京大学校区西侧通过，拟采用盾构隧道方案，线路曲线半径400 m，轨面埋深24 m；北京大学在距离东侧隧道水平距离约200 m处拟建一栋实验楼(见图1)，该实验楼将安装大量精密仪器设备，对环境振动尤其是20 Hz以下低频振动要求较高。地铁16号线将首次在北京采用A型车、8辆编组(简称A8)列车，因此需要准确预测A8列车通过时实验楼内的低频振动响应，为16号线线路规划、减振措施的选择和优化提供依据。

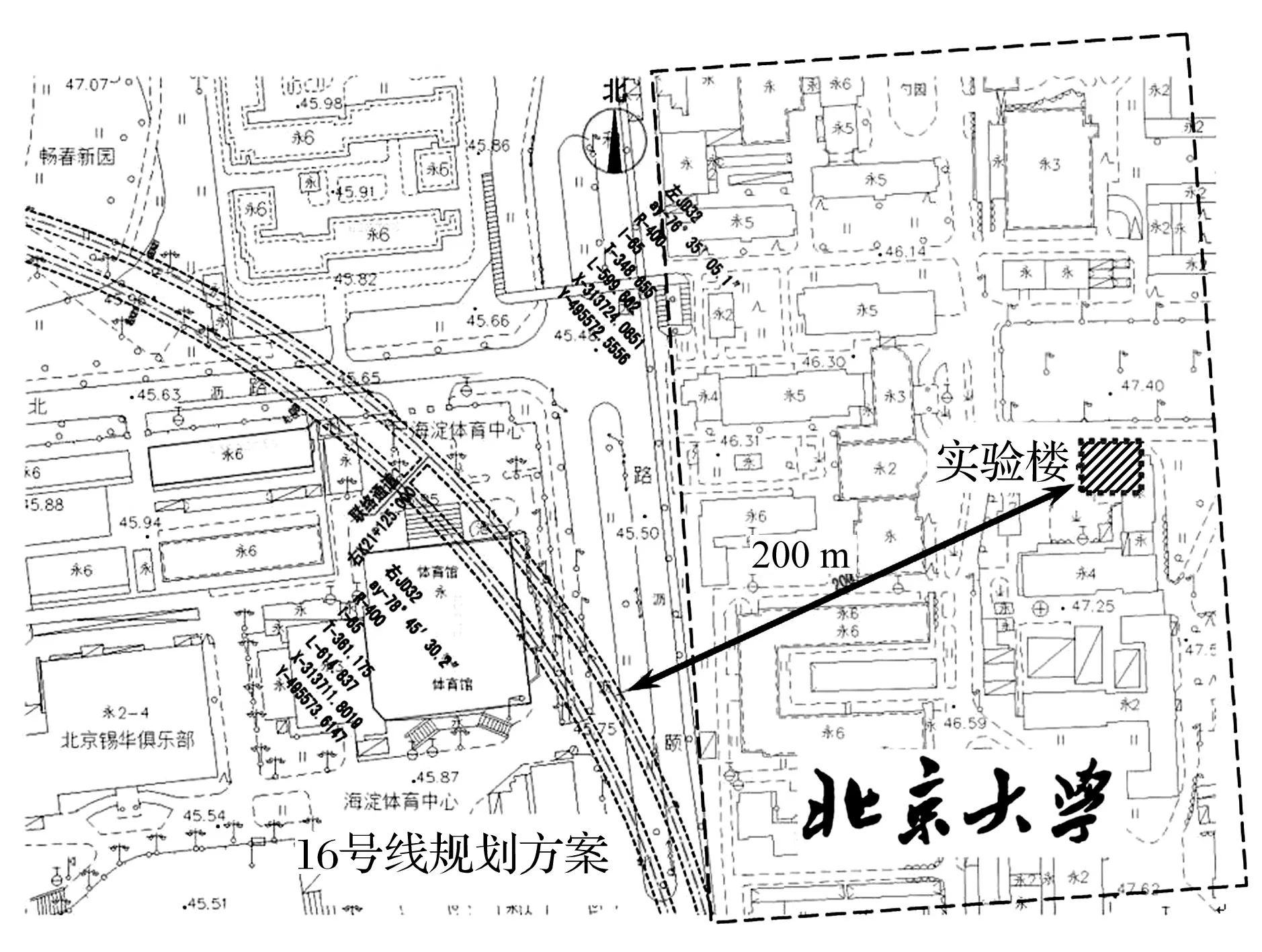
图1 实验楼与规划16号线相对位置关系Fig.1 Relative position between Beijinglaboratory building and planning line 16

1.2 研究方法

为确保动力有限元预测模型的计算精度，采用基于现场实测的“两位校准法”进行校核。如图2所示，首先以已通车运行的北京地铁地铁4号线北大东门—圆明园区间为对象，建立校准模型；实测地铁4号线隧道壁和地表的振动响应以确保校准模型的预测精度，验证建模方法的正确性。采用相同建模方法，建立地铁16号线预测模型，预测A型地铁列车通过时实验楼内的振动响应。其中预测模型采用的地铁列车荷载，为根据北京地铁4号线(B型车)和上海地铁7号线(A型车)的钢轨振动响应时程，通过数定荷载法计算所得。

2 动力有限元模型建立

2.1 数值模型

根据北京地铁4号线、16号线北大段的具体情况分别建立校准模型(见图3(a))和预测模型(见图3(b))。

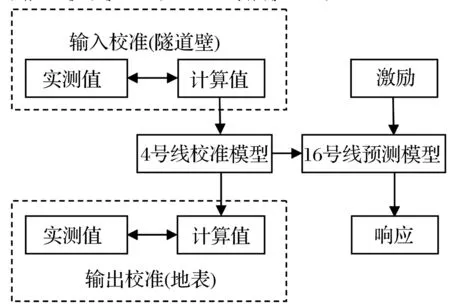
图2 两位校准预测法思路Fig.2 Two-position calibration method

图3 轨道-隧道-土层-建筑基础耦合动力有限元模型Fig.3 Coupled-dynamic-finite-element model of track-tunnel-soil-building foundation system

考虑计算精度、地表预测点与地铁线路中心线间距、地铁线路曲线线形和地铁列车全列长度合理反映等因素，模型范围为360 m×50 m×160 m，采用黏弹性人工边界，结构阻尼采用瑞利阻尼[11]。根据地质勘探结果，按照土层剪切波速的变化范围，将地铁4号线、16号线北大段附近土层结构简化为七层水平层状构造，剪切波速、压缩波速和密度随土层深度变化如图4所示。浮置板道床横断面面积为1.302 m2，钢弹簧按1.2 m间距布置，每个钢弹簧的刚度为5.3 MN/m。计算时，取浮置板动弹模4.2 MPa×104 MPa，泊松比0.3，密度2 500 kg/m3；隧道衬砌厚度0.3 m，动弹模为3.5 MPa×104 MPa，泊松比0.25，密度2 500 kg/m3；隧道基底回填混凝土动弹模为2.85 MPa×104 MPa，泊松比0.3，密度2 500 kg/m3。

根据敏感目标环境振动要求，仅需要分析20 Hz以下的振动响应，动力计算采用时域直接积分法求解，选用Newmark-β隐式积分法实现，时间步长Δt=0.018 s(对应于分析截止频率为27.78 Hz)。

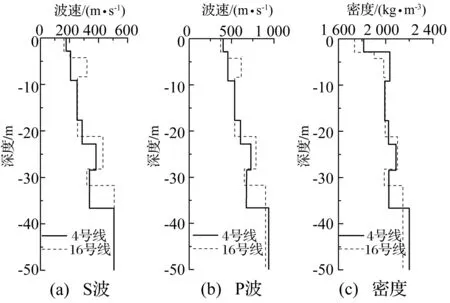
图4 剪切波速、压缩波速和密度随地层深度变化图Fig.4 Changes of shear wave velocity, compression wave velocity and density with layer depth

2.2 荷载确定

由于16号线临近北大段为曲线段，需要考虑列车的垂向荷载及横向荷载。将列车简化为一个二系弹簧-质量系统(见图5)。考虑地铁车辆沿纵向和横向的对称性，取一个转向架的一侧进行分析。根据文献[10]得到沿钢轨纵向均匀分布的列车振动线荷载数定表达式为

Fv(t)=KnMPv(t)/L

(1)

Fh(t)=KnMPh(t)/L

(2)

式中:K为修正系数，一般取1；n为每节列车的转向架数；M为列车的编组数;Pv(t)为垂向轮轨力;Ph(t)为横向轮轨力;L为每节列车的长度。根据所提供的车辆参数情况，一般取n=2个、M=6节。对于B型车：L=19.52×6=117.12 m;对于A型车：L=23.77×6=142.62 m。垂向、横向轮轨力分别为

(m+M1+M2)g+

(3)

(4)

质量体之间的相对位移分别为：ξ1=z1-z0，ξ2=z2-z1，ξ3=z3-z2，ζ1=x1-x0，ζ2=x2-x1，ζ3=x3-x2。

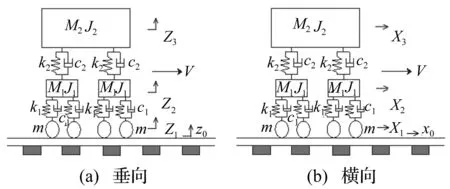
图5 地铁列车振动分析简化模型Fig.5 Simplified model of metro trains

将北京地铁4号线、上海地铁7号线测试得到的钢轨加速度进行数定后，输入式(1)～式(4)，可得模拟B、A型地铁列车振动荷载。根据既有的测试成果[12]，结合本文对20 Hz以下频段的预测目标，用得到的列车荷载进行保频变换，得到用于数值模拟计算的0～27.78 Hz频段的列车荷载时程，如图6和图7所示。

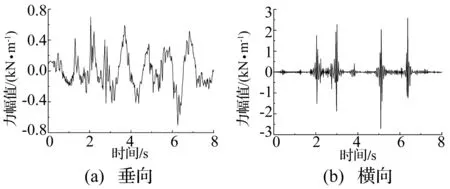
图6 计算用B型车振动荷载Fig.6 B-type train loads using in simulation

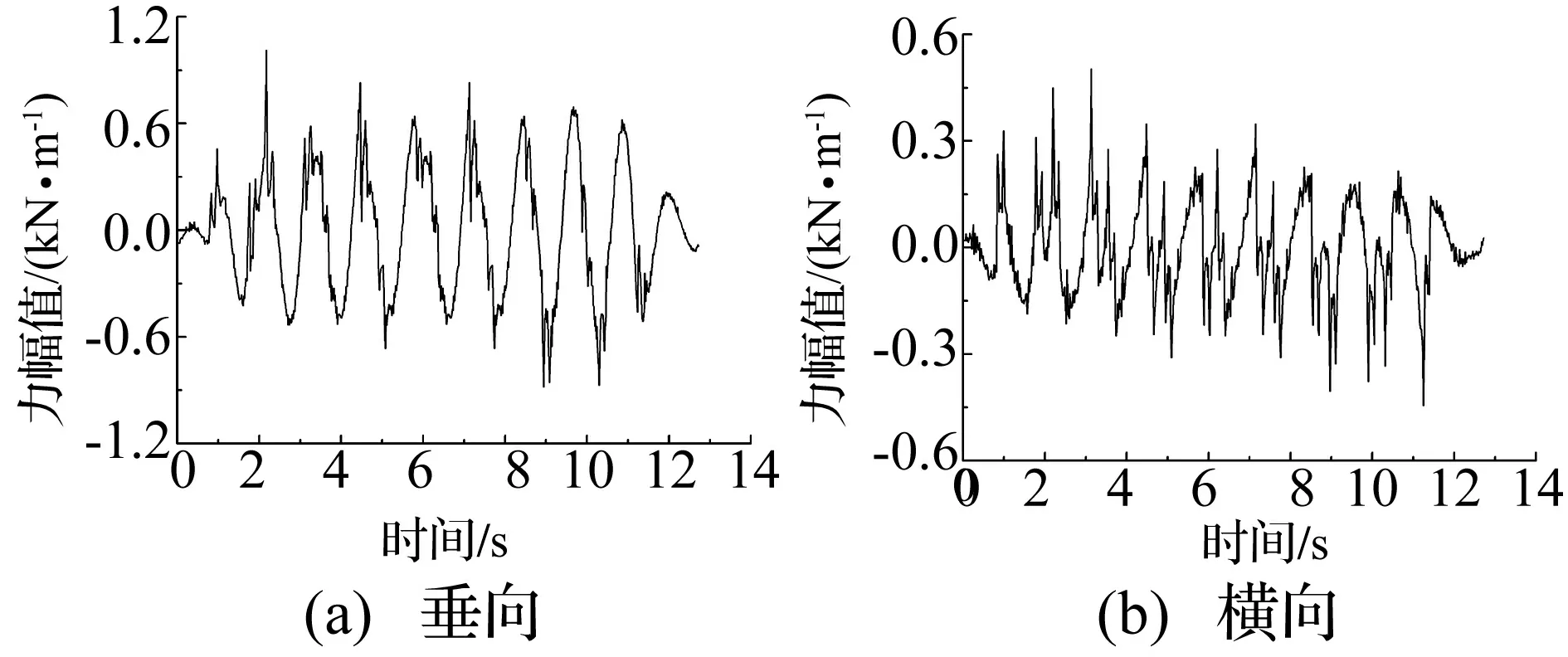
图7 计算用A型车振动荷载Fig.7 A-type train loads using in simulation

3 地铁4号线模型的两位校准

3.1 预测模型荷载输入校核

将区间隧道壁处作为“校准点”，将振动源强的实测结果、地铁列车单线通过时预测模型的计算结果分别进行时程、频谱及1/3倍频程谱分析对比，依此对预测模型中荷载输入的B型地铁列车振动荷载进行校核。由于本文重点进行1～20 Hz频段的低频振动预测，因此在分析与对比之前，将计算结果和实测结果均进行了低通滤波处理，上限截止频率均为20 Hz。

图8和图9分别为北京地铁4号线隧道壁振动响应实测、预测值的时程和1/3倍频程曲线。可以看出二者在时域内处于同一数量级且振动量比较接近；在1/3倍频程曲线上，大部分频段吻合良好。本文得到的B型车荷载可作为地铁4号线运行引起场地振动影响预测模型中的荷载输入。

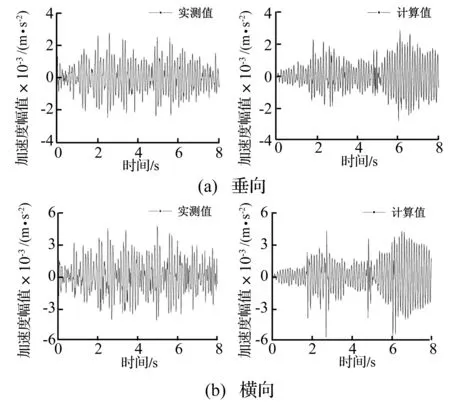
图8 隧道壁“校准点”振动加速度时程对比Fig.8 Comparison of acceleration time history on the tunnel wall

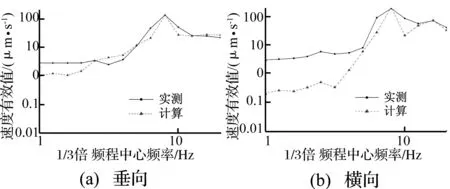
图9 隧道壁“校准点”振动加速度1/3倍频程谱对比Fig.9 Comparison of acceleration 1/3 octave spectrum on the tunnel wall

3.2 地表响应输出校准

在地铁4号线校准模型中，选定距离振源水平距离150 m和200 m地表点作为“校准点”。进行自由场地振动的现场测试，同时提取地铁列车单线通过时，“校准点”处X向(即南北向/SN向)、Y向(即东西向/EW向)和Z向(即垂/UD向)振动速度响应时程，利用实测值和计算值的比较对预测模型进行校核，1/3倍频程谱对比结果见图10。由图10可知，计算分析和实测的1/3倍频程谱曲线走势相同，且量值接近，这说明此模型能够进行远场低频振动预测。

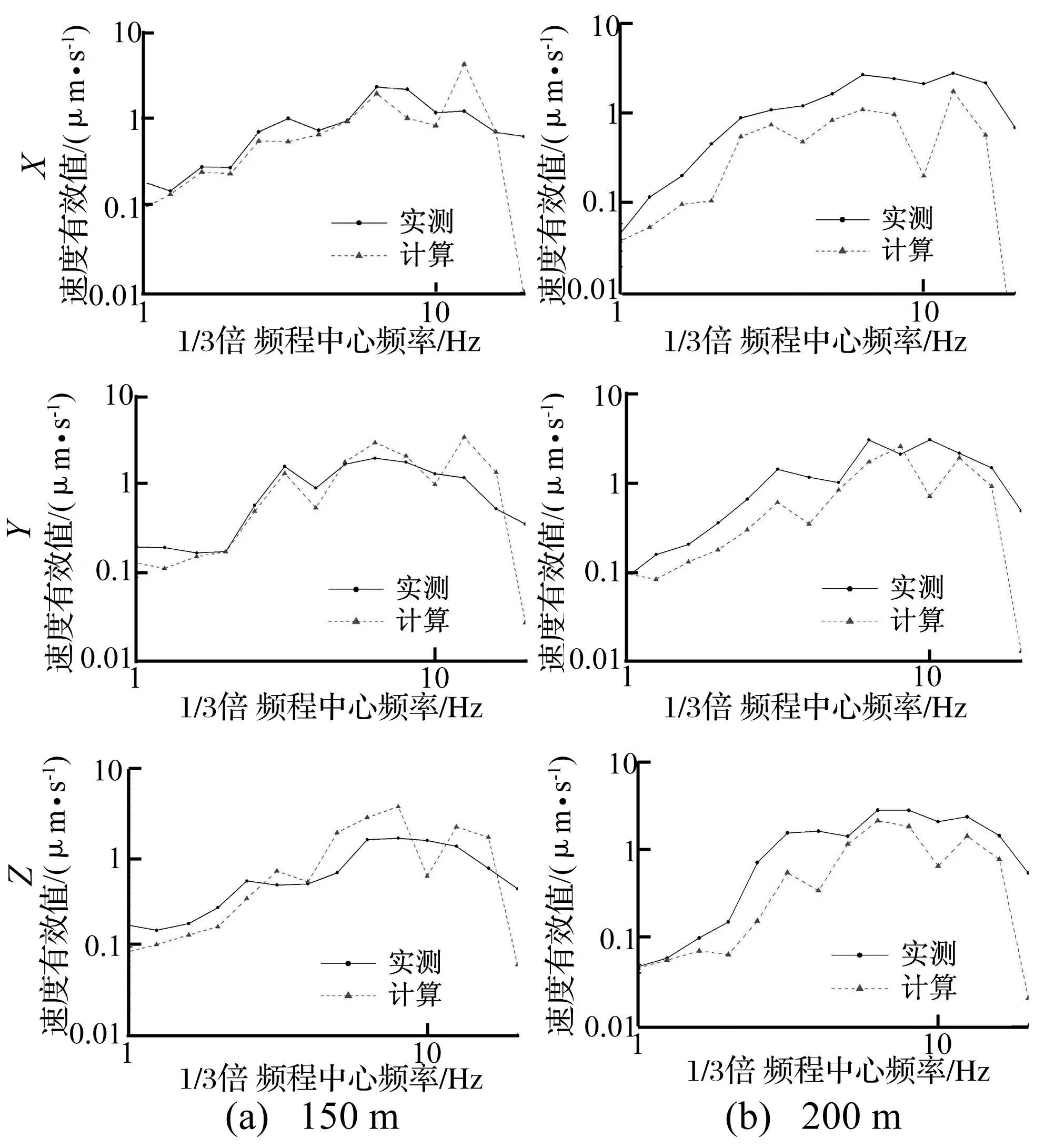
图10 地表“校准点”振动速度1/3倍频程谱对比Fig.10 Comparison of acceleration 1/3 octave spectrum on the ground surface

4 实验楼振动响应预测

采用与校准模型相同的建模方法，输入16号线所在区间的土层参数进行振动响应预测。地铁16号线线路中心线与北大在建实验楼内精密仪器放置处的直线距离约为215 m。将实验楼外地表点定义为“预测点”，距线路中心线间的距离为190 m。预测过程中，分别考虑单、双线列车运行的影响，结果见图11，并与精密仪器VC振动标准进行了比较。

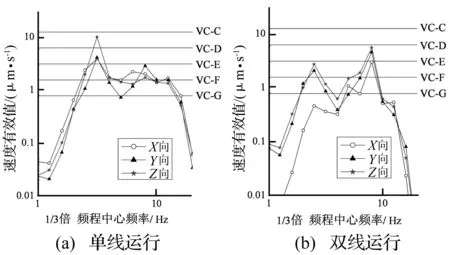
图11 单双线运行时预测结果Fig.11 Prediction results of single or double trains passing

由图11可知:①单线运行时，10 Hz以下频段3个方向的振动均未超过VC-C标准；对于环境振动要求严格VC-D及以上的仪器，则需要采取减振措施，尤其需要注意3 Hz的振动峰值，如果能消除此峰值，则环境振动将能满足VC-E标准；②双线运行时，由于振动波的相互叠加和抵消，导致预测点振动响应在部分频段上有所下降，10 Hz以下频段3个方向的振动均满足VC-D标准；此时9 Hz处存在振动峰值，如能消除此峰值影响，则环境振动将满足更加严格的VC-E标准；③无论单双线地铁列车运行，10～20 Hz频段3个方向的环境振动均满足最严格的VC-G标准，这说明在进行精密仪器隔振处理时，要着重关注10 Hz以下频段的振动响应。

5 结 论

本文利用两位校准法，研究了地铁列车运行的远场低频振动预测模型，并对16号线北大段的环境振动进行了预测分析，结论如下：

(1)将地铁列车简化为二系弹簧-质量系统，利用实测钢轨加速度并通过保频变换得到的地铁A、B型车的计算用垂向、横向振动荷载，能够满足低频振动预测精度的要求。

(2)利用地表实测数据对振动预测模型进行校核，调整仿真模型输入参数，得到了能够进行远场低频振动响应的预测模型。

(3)根据预测结果，地铁16号线使用钢弹簧浮置板后，地铁列车单、双线运行时北大新建实验楼预测点处的地表振动响应：10～20Hz频段满足最严格的仪器环境振动标准VC-G；10 Hz以下频段，单线运行时仅满足VC-C标准，而双线运行时可满足VC-D标准。因此在进行精密仪器隔振处理时，要重点隔离10 Hz以下频段的振动响应。

致谢：感谢北京城市快轨建设管理有限公司、北京市政设计研究总院提供地铁隧道设计数据及土层材料参数，感谢中国铁道科学研究院提供北京地铁4号线、

上海地铁7号线的振源实测数据；感谢中国电子工程设计院提供北京大学场点振动实测数据。

[ 1 ] Office of Planning and Environment, Federal Transit Administration (FTA), U.S. Transit noise and vibration impact assessment:NSN 7540-01-280-550[S]. Washington:[s.n.], 2006.

[ 2 ] 中华人民共和国环境保护部. 环境影响评价技术导则——城市轨道交通:HJ 453—2008[S]. 北京：中国环境科学出版社, 2008.

[ 3 ] 王另的，张斌，户文成，等. 北京地铁环境振动预测模型[J]. 城市轨道交通研究,2013, 16(6): 101-106. WANG Lingdi, ZHANG Bin, HU Wencheng, et al. Prediction model for metro-induced environment vibration in Beijing[J]. Urban Mass Transit, 2013, 16(6): 101-106.

[ 4 ] BALENDRA T, CHUA K H, LO K W, et al. Steady-state vibration of subway-soil-building system[J]. Journal of Engineering Mechanics, ASCE, 1989, 115(1): 145-162.

[ 5 ] CLOUTEAU D, ARNST M, AL-HUSSAINI T M, et al. Free field vibrations due to dynamic loading on a tunnel embedded in a stratified medium[J]. Journal of Sound and Vibration, 2005, 283(1/2): 173-199.

[ 6 ] YANG Y B, HUNG H H. Soil vibrations caused by underground moving trains[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2008, 134(11): 1633-1644.

[ 7 ] 马龙祥. 基于周期-无限结构的车轨耦合及隧道-地层结构振动分析模型研究[D]. 北京: 北京交通大学, 2014.

[ 8 ] WOLF S. Potential low frequency ground vibration (< 6.3 Hz) impacts from underground LRT operations[J]. Journal of Sound and Vibration, 2003, 267(3): 651-661.

[ 9 ] GUPTA S, LIU W F, DEGRANDE G, et al. Prediction of vibrations induced by underground railway traffic in Beijing[J]. Journal of Sound and Vibration, 2008, 310(3): 608-630.

[10] 孙晓静. 地铁列车振动对环境影响的预测研究及减振措施分析[D]. 北京：北京交通大学, 2008.

[11] 刘更. 结构动力学程序设计[M]. 北京: 国防工业出版社, 1993.

[12] 楼梦麟，贾旭鹏，俞洁勤. 地铁运行引起的地面振动实测及传播规律分析[J]. 防灾减灾工程学报, 2009,29(3): 282-288. LOU Menglin, JIA Xupeng, YU Jieqin. Field measurement and analysis of gound vibration induced by subway trains [J]. Journal of Disaster Prevention and Mitigation Engineering, 2009,29(3): 282-288.

Prediction of metro train-induced low frequency vibration responses in far field

SUNXiaojing1,YUANYang2,MAMeng1,LIUWeining1

(1. School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China； 2.Tianjin Urban Planning & Design Institute, Tianjin 300201, China)

Since the micro vibration in low frequency range has significant influence on precision instrument, to predict the low frequency vibration impact induced by metro trains becomes a challenge problem. Taking the case of Beijing Metro Line 16 passing below Peking University as an example, quantitative prediction of metro train-induced low frequency vibration responses in far field was researched in this paper by using a two-position calibration method. In the research, the simulated train loads were firstly obtained by frequency-hold transforming with the measured rail acceleration. Then, the FEM model of Beijing Metro Line 4 was established, and the input load and parameters were calibrated by compared with the measured data collected from tunnel wall and ground surface. Finally, the FEM model of Line 16 was established to predict low frequency vibration effects. The results show that (1) the simulated train loads and the FEM model can provide sufficient prediction accuracy in low frequency range. (2) in the case of Beijing metro line 16 passing below Peking Laboratory Building, the steel-spring-floating-slab is able to provide great vibration isolation performance, which can meet the required limit of instrument in the range of 10-20 Hz, but in the range of 0-10 Hz, the vibration is just under the VC-C limited standard; therefore, in the range of 0-10 Hz, extra treatments are needed on buildings and instruments.

low frequency vibration; far field vibration; two-position calibration method; dynamic finite element; train load

国家自然科学基金项目(51408033)

2016-03-10 修改稿收到日期：2016-06-11

孙晓静 女，博士，讲师，1978年12月生

TB533+.2;X966

A

10.13465/j.cnki.jvs.2017.04.031