电流变夹层板控制系统的传感器优化布置

陈春强, 陈 前

(南京航空航天大学 机械结构力学及控制国家重点实验室，南京 210016)

电流变夹层板控制系统的传感器优化布置

陈春强, 陈 前

(南京航空航天大学 机械结构力学及控制国家重点实验室，南京 210016)

为了解决ER夹层板系统的模态控制的实用性问题，研究了悬臂板模态坐标估计和传感器定位问题。按照变刚度模态控制算法的要求，给出了离散坐标下模态坐标估计的方法；根据连续结构的振型分析，分析传感器定位计算，建立了数学优化模型；按照模态动能法初步筛选后，枚举得到传感器优化布置方案，并且从估计精度和控制效果两个角度进行了布置方案的算例验证。结果表明，优化的传感器布置能在较少的数目下，模态坐标估计满足模态控制算法的输入需求。

模态控制算法；模态坐标估计；传感器布置优化；MAC检验

电流变液夹层板(Electrorheological sandwich plate，ER夹层板)是一种振动控制新型的智能结构，具有集被动控制安全、可靠和半主动控制适应性强、控制效果显著等特点。但这种结构与工程应用还有距离，还有某些实用性问题需要解决，例如简单开关变刚度控制算法难以在连续结构(梁、板)取得较好的控制效果，而在模态坐标下设计控制算法是一个有效的解决方案[1]。而要实现模态控制，首要问题就是获取模态坐标。由于现实技术条件限制，不可能在所有自由度上布置传感器，还应当用尽量少的传感器获得最有效的信息，以降低系统的复杂度；此外，研究[2-5]指出，夹层板结构高阶模态的振动能量将通过芯层的剪切变形得以消耗，也就是说控制器不需要所有模态的信息。因此，在ER夹层结构的半主动控制系统中，对传感器优化布置从而实现模态坐标估计，特别是低阶模态是很有必要的。

模态坐标估计包含了两个步骤，估计手段和传感器定位。模态坐标估计包括模态观测器和模态滤波两种方法[6]，对于已经建立了有限元模型，采用离散型模态滤波器是合适的，也利于数值检验。模态坐标估计的传感器定位，通常是基于结构振型相关。对于复杂结构的传感器定位，振型通常是用有限元建模求得，是各节点的离散值，直接用于传感器定位存在困难，插值法[7]具有优化模型清晰和搜索快速的特点。

本文关注了ER夹层控制系统的关键技术模态控制和模态坐标估计。首先，基于单自由度的开关控制策略介绍了适用于板的模态控制算法；随后，采用了离散系统的模态坐标估计方法，基于传感器定位的优化模型，给出了不同数目下的传感器布置方案；最后，用估计值与精确值对比和控制效果对比两种手段，验证了模态估计方案、传感器布置的有效性。

1 ER夹层板控制系统模型以及模态控制算法

如图1所示的电流变液夹层板振动控制系统，将ER夹层处划分为4节点7自由度单元，限于篇幅，有限元建模过程从略，得到如下的ER夹层板系统的控制方程

(1)

式中:零电场下的复刚度矩阵K*=K1+jK2，G(E)是由外加电场强度决定的刚度变化系数阵。

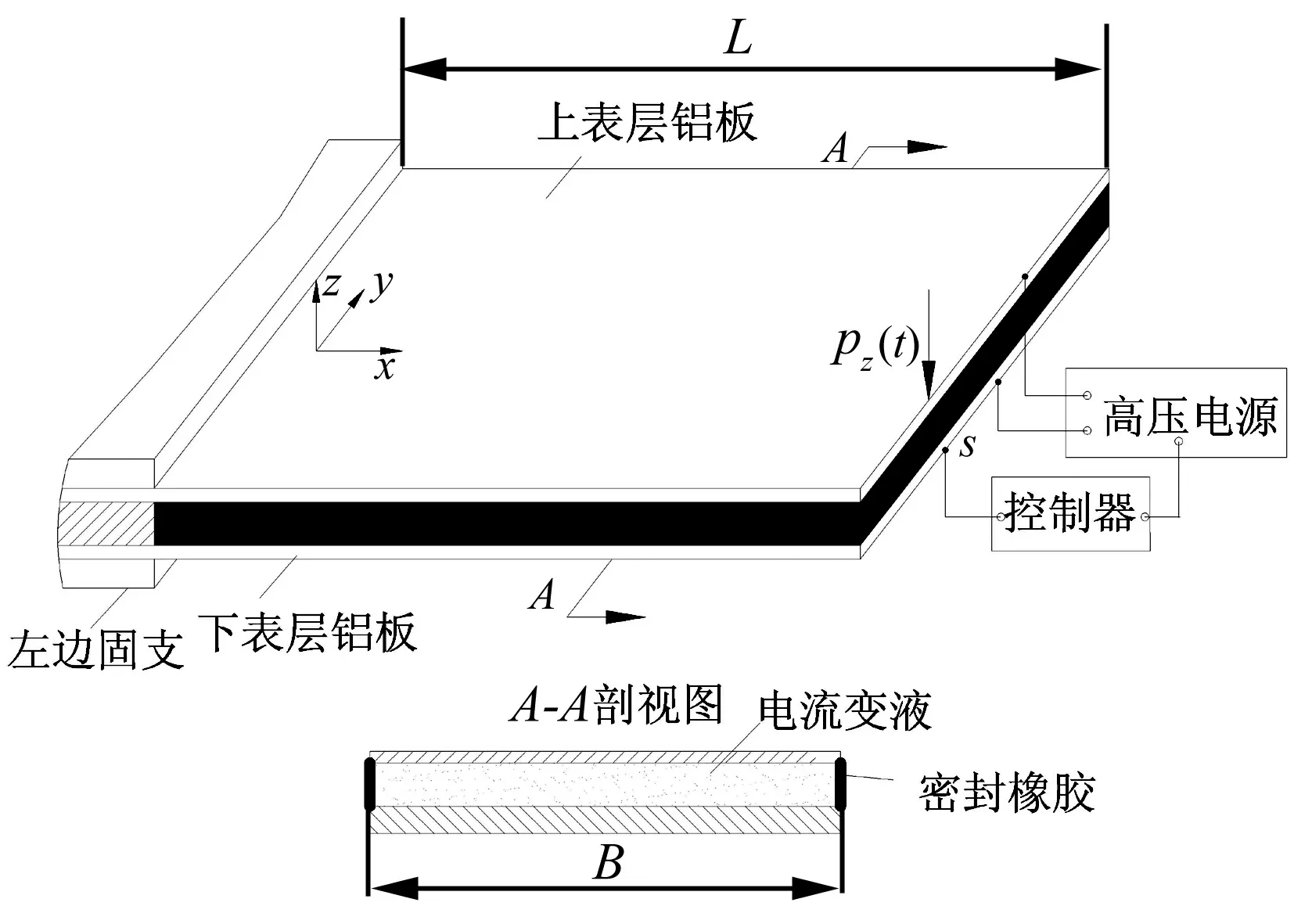
图1 电流变夹层板振动控制系统Fig.1 The sandwich plate with an ER fluid core and a constraining layer

开关控制算法[8](Bang-Bang control，also called On-Off control)，是变刚度控制(Active Variable Stiffness，AVS)中最成熟的算法，其以位移和速度输入，当两者符号一致时，控制输出为1，系统附加上刚度；否则控制输出为0，即撤去附加刚度，从而舍弃相应的弹性应变能。从以上描述可知，变刚度控制利用是刚度实部的变化，那么可以做以下模型简化，略去刚度的虚部，即

(2)

记Φ是K1、M的关于M归一化了的特征向量阵，用δ=ΦQ变换上式，并两端左乘ΦT，可得

(3)

式中:左边两项的系数矩阵均是对角阵;第三项系数阵ΦTK1G(E)ΦT一般而言不会是严格对角的，但研究[9]表明，ER夹层板结构的固有振型基本不随电场强度变化而变化，这说明用任意电场工况下的振型进行解耦，得到的第三项系数阵也是对角占优的，略去其非对角元素，有

(4)

式中:fi为ΦTF向量的i元素;qi(t)为近似的实模态坐标，在控制中，该值在每个采样周期内实测而得。

在控制算法设计之前，系统相关的参数，如质量矩阵M、刚度矩阵K1以及包含主要振动能量的前p阶模态的振型φ1,φ2,…,φp，应当首先获得。那么，结合控制中监测到的模态坐标，可以获得各阶模态的振动能量U1,U2,…,Up。出于平衡各阶模态的控制需要，引入由模态振动能量确定的权重系数向量Q。模态权重系数向量Q就由这些模态振动能量构成，并进行无量纲化

(5)

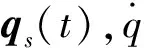
(6)

综合考虑到前p阶次模态的输出要求，控制器输出电场的综合平均值为

(7)

式中，Qs为权重系数向量Q中的元素。

考虑到电场强度有其边界条件限制，即不能超过最高强度Eb且保持非负，所以半主动模态控制算法(Semi-active modal control algorithm)的输出的控制电场是

(8)

2 模态坐标估计

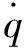
(9)

式中:qr为第r阶模态位移;φr为全体自由度的振型矩阵Φ的第r列。利用固有振型的正交性和关于质量归一化条件，模态坐标可以表示为

(10)

对于复杂的离散结构，模态阶数N很大，通常采用模态截断技术，考虑结构的前n阶模态，n≪N。把由全部自由度的物理位移变换得到的模态坐标认为是精确值。实际控制中，在结构上布置有p个传感器，每个传感器的测得的分别响应为w1,w2,…,wp，即

(11)式中，φs,r为系统的s阶模态向量中第r元素。不计噪声信号，该组响应与式(11)对应相等，解一组线性方程组可得模态位移的估计值，分别把式(10)和式(11)中位移替换成速度，即可得到模态速度的精确值和估计值。

3 传感器定位

3.1 传感器定位计算

利用传感器的输出计算受控结构的模态位移和速度，进而实现模态控制，而传感器的数目和位置对模态位移和模态速度具有很大影响的。所以，需要考虑传感器定位对从传感器测量中提取模态坐标精度的影响。由于有限元方法获得的振型是各节点处的离散值，将其用于传感器定位的优化存在一定的困难，下面参考插值法，给出ER夹层板系统传感器定位优化过程。

选择悬臂板的弯曲振动和面内拉伸的振型函数为容许函数，下表层的振型函数与上表层类似，这里就不列出，即

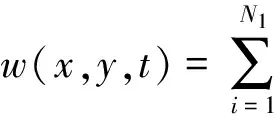
(12a)

(12b)

(12c)

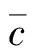
φi(x,y)=X(x)Yi(y)

(13)

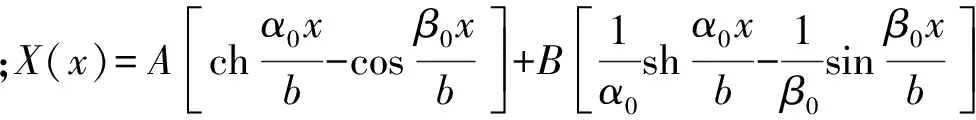
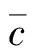
(14)

式中:Φr(x,y)为结构的弯曲振型;ηr(t)为第r阶模态位移。

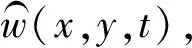
(15)

式中:xj和yj是传感器的位置;G(x,y,xj,yj)是由传感器布置点插值函数。

将式(15)代入式(14)，测量得到模态坐标表示为qr(t)，即

(16)

式(16)也可写成矩阵形式

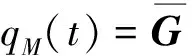
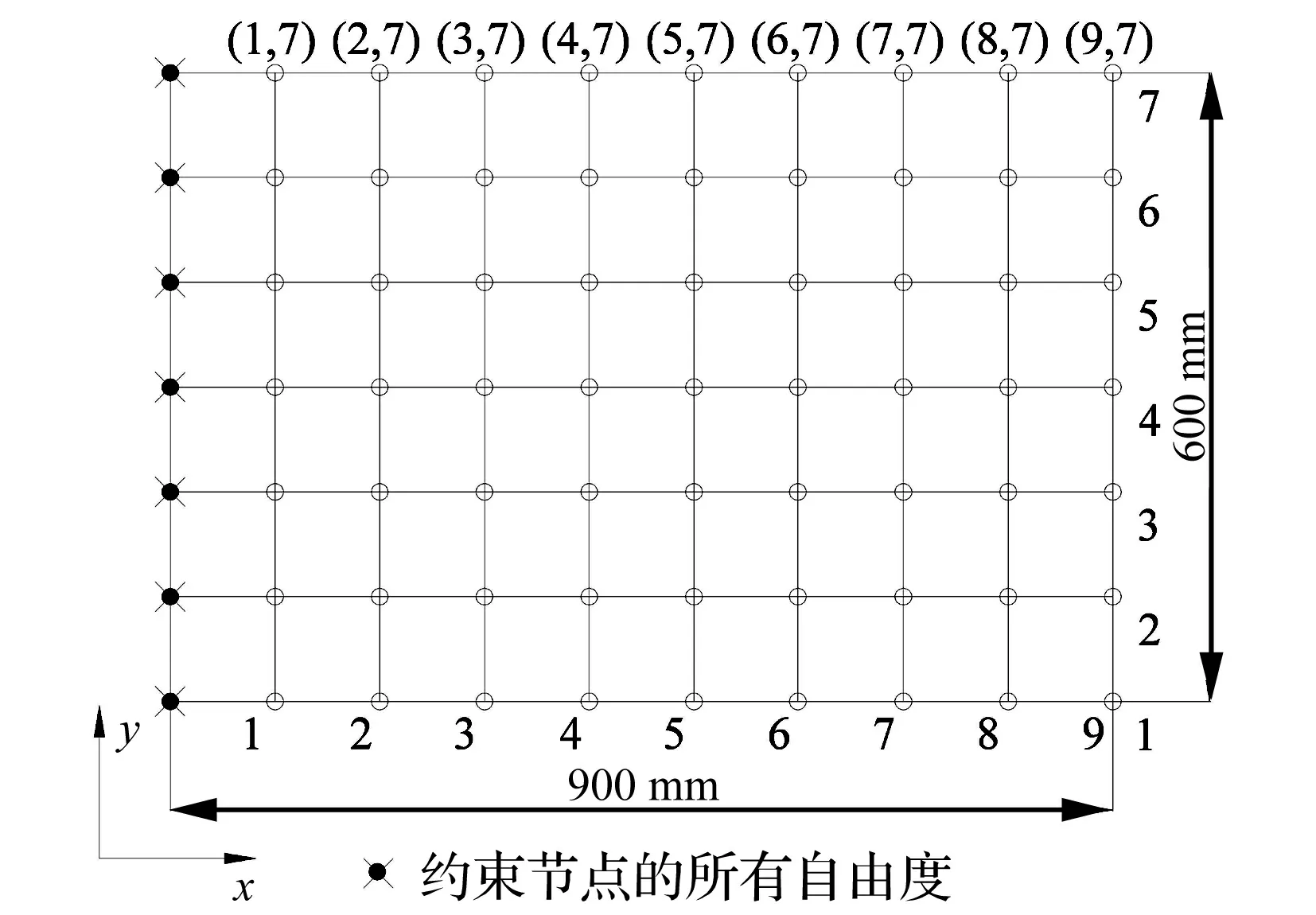
(17)

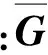
(18)

式中:HM(i,j)=Φj(xi,yi)，i=1,2,…,l;j=1,2,…,m；HR(i,j)=Φm+j(xi,yi),i=1,2,…,l;j=1,2,…;m为量测模态数目;l为传感器数目。

模态滤波的误差

em(t)=ηm(t)-qm(t)=

(19)

忽略测量噪声的影响，传感器的定位问题可以表述为一个优化问题

findxi,yi

(20)

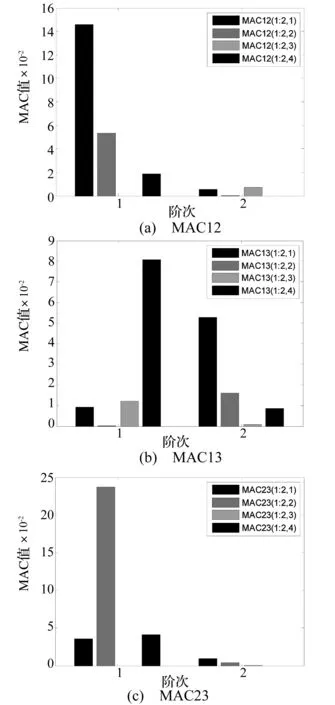
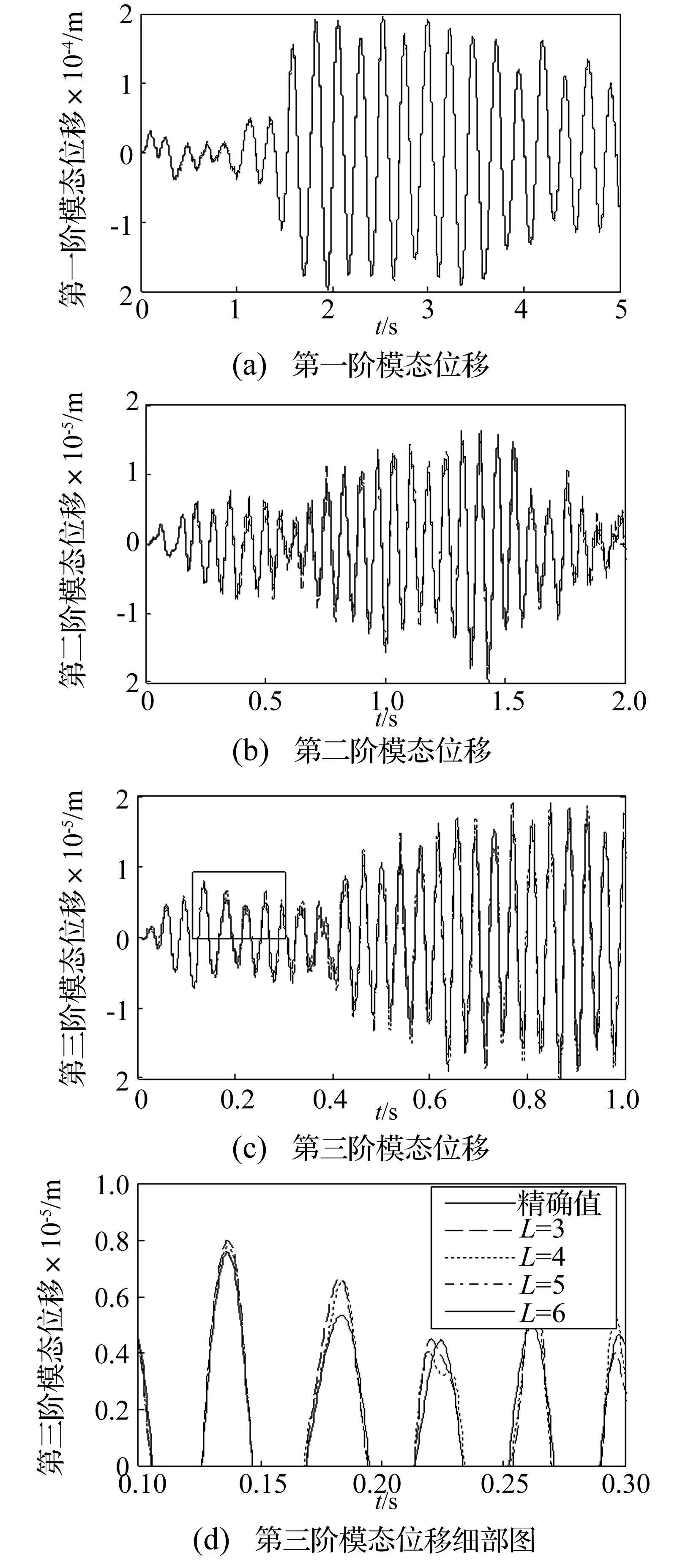
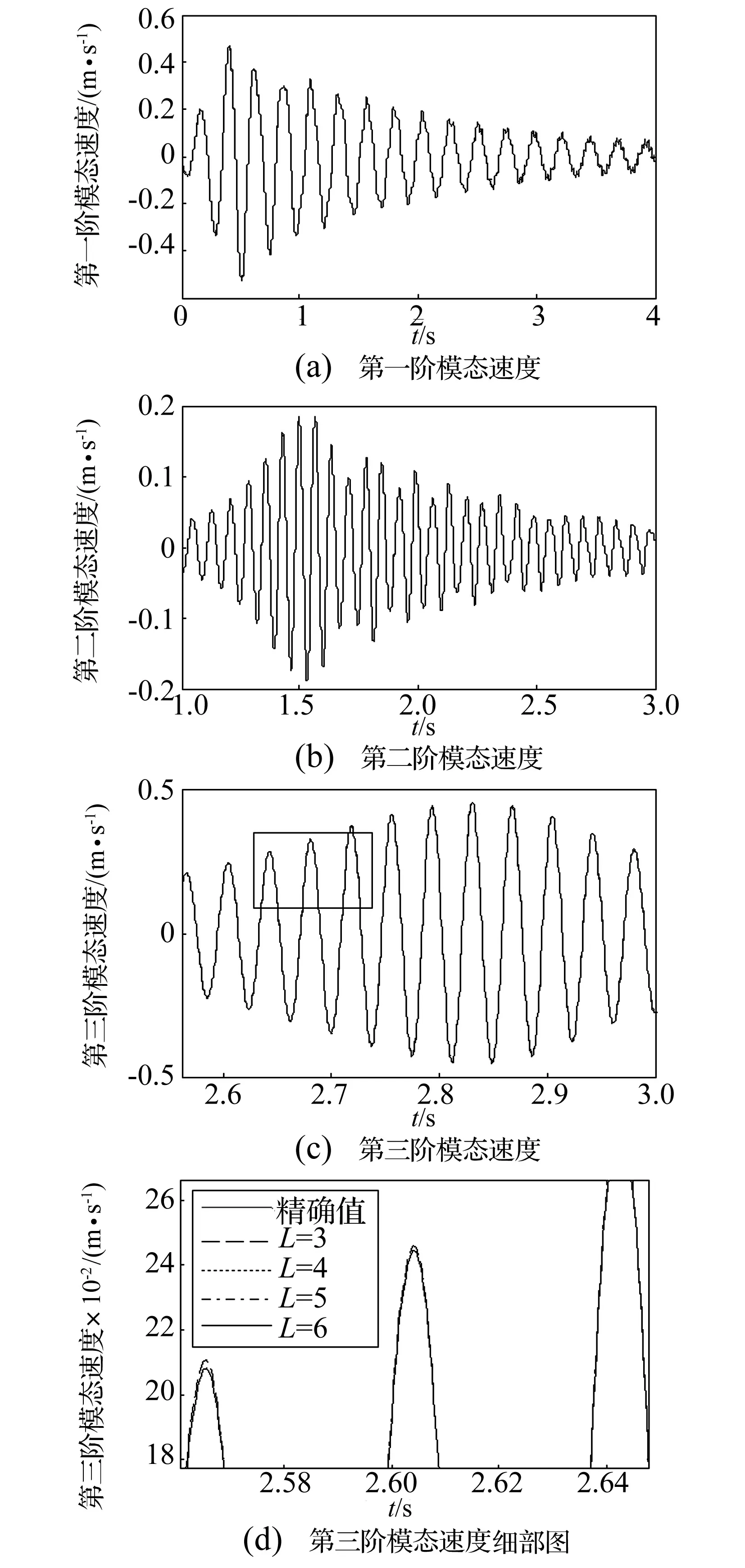
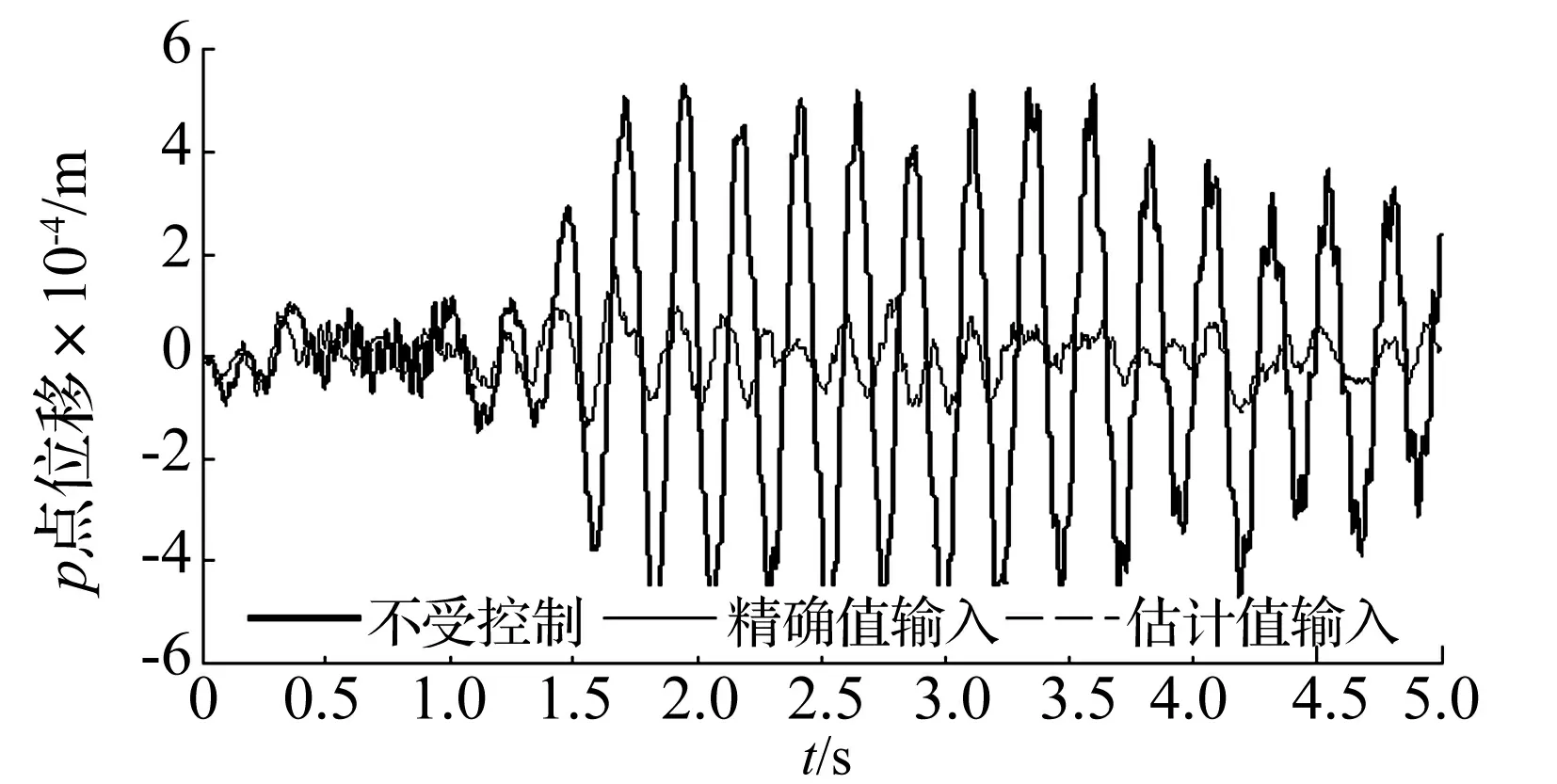
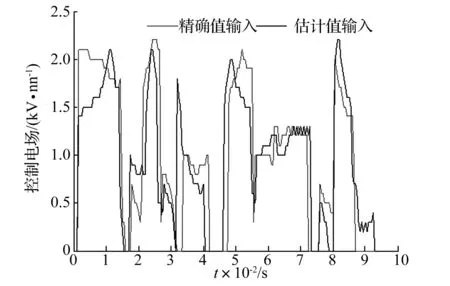
subjectto0

约束条件中，Lx,Ly为ER夹层板在x,y方向上的最大尺寸，在有限元模型中，xi和yi为节点对应的自然数。目标函数J实际上是有量测模态和无量测模态对目标模态误差累积。另外，考虑到低阶模态的响应更大，是控制中模态估计的重点，对目标函数采用了结构模态频率的加权，低阶模态对应的权重更大。为了简便，插值函数G(x,y,xi,yi)可以选用齐次位移形函数。

3.2 传感器优化定位步骤

模态动能法 (Modal Kinetic Energy, MKE)是传感器布置的传统方法，其思想是在模态动能较大的自由度上布置传感器，使其具有较高的信噪比。这里，首先采用MKE方法筛选出对前六阶模态动能较大的位置，缩小优化模型的搜寻范围，然后利用优化模型，即式(20)进行枚举搜索。结合电流变夹层板的控制系统的实际需要，给出传感器的定位、布置和检验流程。

(1)建立ER夹层板结构的有限元模型，模态分析获得全体阶次的振型信息，根据计算结果和控制需求确定监测模态坐标的阶次，这里取前三阶，即传感器的布置数目>3。

(2)按照MKE法，在全体弯曲自由度上筛选出模态动能较大的自由度，每个阶次选择一定数目的自由度，将这些自由度集合起来，并删除重复的自由度，组成传感器的候选自由度。

(3)对候选自由度集合进行组合，构成传感器布置的候选组合，按照式(20)的优化模型，计算所有组合的目标函数值，选取函数值最小的布置组合，传感器数量l分别取为3、4、5和6，测量模态数目m定为3。

(4)采用置信度MAC矩阵(由确立的测点自由度组成的模态向量构成)，对被测模态的交角状况进行判断。

(5)为对控制系统中的传感器布置方案进行验证比较，采用精度对比和控制效果对比两种方法，具体的方法见下文算例中。

4 算 例

如图1所示的ER悬臂夹层板，其几何、物理参数见表1，ER材料参数参考DON[10]的研究。网格数9×6，满铺结构共有441个自由度，其中63个是弯曲自由度，将这些弯曲自由度作为候选点，如图2所示。

取ER夹层板的前三阶模态为监测模态，分别采用MKE方法和优化方法，选取传感器数目为6、5、4、3的情形，可以获得表2所示的优化后的传感器布置方案。

表1 ER夹层板的几何、物理参数

图2 电流变悬臂版的有限元模型Fig.2 The finite element model of ER sandwich plate

数目方法传感器位置节点编号目标函数值J/%6MKE优化(6，1)(6，7)(7，1)(7，7)(8，1)(8，7)(8，6)(8，3)(8，2)(6，4)(4，2)(4，7)2．70．55MKE优化(6，1)(7，1)(7，7)(8，1)(8，7)(8，6)(8，2)(6，4)(4，7)(4，1)2．10．44MKE优化(4，2)(4，6)(9，2)(9，6)(8，6)(7，7)(7，1)(4，1)3．30．93MKE优化(8，6)(8，2)(9，6)(8，4)(7，7)(5，2)3．20．8

表2中第四列反映的是各种布置方案下的目标值即量测误差J，结果显示，优化的布置方案能大幅降低量测误差。需要指出的是，由于量测模态数目与传感器数目一致，传感器数目越多，需要积累误差的模态数目也越多，所以该结果未能完全反映出传感器数目增加对估计精度的有效性。

在选择测点时有必要使测量的模态向量保持较大的空间交角，从而尽可能的把原来模型的特性保留下来[11]，是进行MAC检验的出发点。按照表2给出的传感器布置方案，对前三阶模态的MAC12以MAC13及MAC23值比较，如图3所示，每个图的左右两部分四个值分别对应着传感器数目编号3、4、5和6。图中可以看出MKE法布置方案确定的MAC阵的值较大，该方法获得各阶模态之间的正交性较差；而优化方法时的MAC阵的值较小，特别是MAC12和MAC23的值更接近于0，也表明了优化方法监测模态之间具有更好的正交性和独立性。另外也注意到传感器数目对MAC值的影响较为复杂，MKE法和优化方法中都没有明显的规律，在MAC13的图中，两种方法布置传感器数目的影响几乎是相反的，这也体现了传感器布置数目和位置的随机性。

颜晓晨忙把手中的杯子和碟子都放下，站起来，从角落里走了过去，恭敬地打招呼：“程先生，晚上好！想喝点什么？”

图3 不同优化方法和数目下模态间MAC值比较Fig.3 The comparison chart of MAC value

在ER夹层板控制系统中，采用优化方法得到传感器优化布置的目的是快速、准确地获得广义坐标，从而作为控制器的输入，最终在控制效果上得到体现。从这两点出发，下面就几种传感器布置方案，进行模态坐标估计的精度和控制效果的比较。

选用激励信号，随机激励(2～50 Hz, 5 s)和宽频快扫频(2～40 Hz,4 s)。首先，把式(10)得到的模态坐标作为对照基准，考察由式(11)估计得到的坐标的准确性，图4比较了随机激励下模态位移估计的精度，由于快扫频激振工况下，模态位移估计得较为准确，而模态速度差异较明显些，所以取模态速度对比如图5所示。由于三种工况下的测量值和估计值都较为接近，把图4(c)和图5(c)框中的细部放大，对应地获得图4(d)和图5(d)。

图4 随机激励下，模态位移估计值与精确值对比Fig.4 Comparison between estimate and exactitude value of the modal velocity

图5 宽频带快扫频激励下，实测模态速度坐标与准确值对比Fig.5 comparison between estimate and exactitude value of the modal velocity

由图4和图5可知，两种工况下，四种布置传感器方案估计的模态坐标的精度均较高，特别是第一阶模态坐标的估计值几乎与精确值相等，这主要是该阶模态坐标的绝对值较大，估计的误差较小，同时也是优化模型中权重对低阶模态倾斜的结果。而估计所得的第二、三阶的模态坐标，相对精确值的误差稍大些，需要指出的是，这里的误差体现在幅值的微小差异，相位信息是较为准确的。另外，从细部图图4(d)、图5(d)可以看出传感器数目3时的误差最大，而布置5、6个传感器时误差很小，特别是6个传感器方案的估计模态坐标曲线时几乎与精确值曲线重合。

为直观体现传感器布置对控制系统的影响，采用式(8)给出的变刚度模态控制算法，选用模态坐标的精确值和估计值作为控制器输入。此处为体现差异，模态坐标的估计值是由精度最低的3传感器布置方案得到的。激振载荷选用随机激励，控制电场上限Eb=3 kV/mm，控制模态为前三阶，为方便比较，选取统一测点p的位移时域响应对比，如图6所示。

图6 随机激励下，模态坐标精确值和估计值输入时的控制效果Fig.6 Comparison between estimate and exactitude value for the control input

图7 控制电场时程曲线Fig.7 Comparison of control electric field strength

图6反映了两点内容，首先，变刚度模态控制能在全时域范围内抑制振动水平；其次，精确值和估计值输入下的控制响应几乎是重合的，说明控制效果是极其相似的，说明即便是估计精度较低的优化布置方案也能得到类似于精确输入的控制效果。为进一步说明该现象，图7给出了控制中电场强度时域曲线，从图中可以看出，两种输入下的控制电场虽然有所不同，但主要位置、构形是一致的，这也是控制后响应相似的原因。究其根源，图4、图5中已经表明传感器布置估计出的模态位移、速度的相位都是较为准确的，也就是能量占优的模态识别，而模态控制算法对而模态控制算法对输入的模态坐标精度要求不高。

5 结 论

通过数值计算进行了估计精度和控制效果的验证，验证了本文模态坐标估计方案和传感器定位方法的有效性，主要得到了以下结论：

(1)变刚度模态控制算法能适应复杂激励工况，取得较好的振动控制效果，如图6所示。

(3)当控制输入的精度不高时，控制仍然能取得令人满意的效果，显示了模态控制算法对系统输入精确性要求较低，即该算法具备一定的鲁棒性能。

[ 1 ] 吴波, 刘汾涛, 魏德敏. 变刚度半主动控制结构的拟振型分解法[J]. 华南理工大学学报(自然科学版),2002,30(9): 85-90. WU Bo, LIU Fentao, WEI Demin. Approximate mode decomposition method for structures with semi-active variable stiffness systems[J]. Journal of South China University of Technology(Natural Science Edition), 2002, 30(9): 85-90.

[ 2 ] YEH J Y, CHEN L W. Finite element dynamic analysis of orthotropic sandwich plates with an electrorheological fluid core layer[J]. Composite Structures, 2007,78(3):368-376.

[ 3 ] YEH J Y. Vibration control of a sandwich annular plate with an electrorheological fluid core layer[J]. Smart Mater Struct, 2007, 16(3): 837-842.

[ 4 ] 应祖光，陈海锋.磁流变黏弹性夹层板随机激励下的微振动响应特性[J].振动与冲击，2012,31(19): 6-14. YING Zuguang,CHEN Haifeng. Micro-vibration response characteristics of a randomly excited sandwich plate with MR visco-elastomer[J]. Journal of Vibration and Shock,2012, 31(19): 6-14.

[ 5 ] 张冲,鲁刘磊. 磁流变液矩形夹层板的动力特性分析[J].机电工程技术,2013,42(3):15-20. ZHANG Chong, LU Liulei. Dynamics analysis of rectangular sandwich plates with magnetorheological Fluid[J]. Mechanical & Electrical Engineering Technology, 2013, 42(3):15-20.

[ 6 ] 顾仲权, 马扣根, 陈卫东. 振动主动控制[M]. 北京:国防工业出版社,1997.

[ 7 ] BRAUH H, CHOE K. Sensor placement in structural control[J]. Journal of Guidance Control and Dynamics, 2015, 13(3):524-533.

[ 8 ] CHOI S B，PARK Y K， CHEONG C C．Active control of intelligent composite laminate structures incorporating an electro-rheological fluid[J]．Intelligent Material Systems and Structures，1996，7(7):411-419.

[ 9 ] 孟光, 鲁宏权, 任兴民. 电流变液夹层板结构动态特性及振动控制的实验研究[J].航空学报,1998,19(4): 456-461. MENG Guang, LU Hongquan, REN Xingmin. Experiment study on the dynamic characters and vibration control of a sandwich plate with electro-rheological fluid[J]. Acta Aeronautica et Astronautica Sinica, 1998, 19(4):456-461.

[10] DON D L, COULTER J P. An analytical and experimental investigation of electrorheological material based adaptive beam structures[J]. Journal of Intelligent Material Systems & Structures, 1995, 6(6): 846-853.

[11] 杨雅勋，郝宪武，孙磊. 基于能量系数-有效独立法的桥梁结构传感器优化布置[J].振动与冲击，2010,29(11): 119-134. YANF Yaxun, HAO Xianwu, SUN Lei. Optimal placement of sensors for a bridge structure based on energy coefficienent-effective independencen method[J]. Journal of Vibration and Shock, 2010,29(11): 119-134.

Optimal sensor placement in the control system of a sandwich plate with electro-rheological fluid

CHENChunqiang,CHENQian

(State Key Laboratory of Mechanics and Control of Mechanical Structures, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

Modal control algorithm and optimal sensor placement for an electrorheological sandwich plate under semiactive variable modality stiffness vibration control were investigated. First of all, on the modal coordinate, a modal coordinate estimation method was obtained according to the demand of the control algorithm. And then, an optimal model was developed based on the analysis of vibration mode shape. Lastly, complete enumeration was adopted after filtering the structure nodes and these optimal configurations were verified by two kinds of comparisons of precision in calculation and vibration control. The numerical example shows that this modal coordinate estimation from the configuration with a few sensors can satisfy the demands of modal control algorithm.

modal control algorithm; modal coordinate estimation; optimal sensor placement; modal assurance criterion

中央高校基本科研业务费专项资金资助；江苏高校优势学科建设工程资助项目

2015-05-27 修改稿收到日期：2016-01-21

陈春强 男，博士生,1987年生

陈前 男，教授，博士生导师，1951年生

O328; TP273

A

10.13465/j.cnki.jvs.2017.04.021