离合器摩擦副摩滑过程轴向振动特性研究

王晓燕， 李 杰， 张志凯， 王志勇， 邢庆坤

(1.中国北方车辆研究所 车辆传动重点实验室，北京 100072； 2.北京物资学院 信息学院，北京 101149; 3.北京建筑大学 机电与车辆工程学院，北京 100044)

离合器摩擦副摩滑过程轴向振动特性研究

王晓燕2， 李 杰1,3， 张志凯1， 王志勇1， 邢庆坤1

(1.中国北方车辆研究所 车辆传动重点实验室，北京 100072； 2.北京物资学院 信息学院，北京 101149; 3.北京建筑大学 机电与车辆工程学院，北京 100044)

通过对摩擦副表面结构特征和接触力学等理论的应用, 建立了热变形微观法向单元接触数学模型。采用数理统计和归一化方法, 将微观模型转换成宏观数学模型, 分析了摩擦副法向弹性接触特性, 并引入Kelvin-Voigt (KV)模型, 增加黏弹性接触微分算子, 构建了包含有应力和应变关系的黏弹性接触属性的数学模型, 得到了摩擦副轴向振动数学模型。经仿真分析, 获得了摩擦副摩滑过程的振动特性, 同时对不同转速条件下的摩擦副摩滑过程轴向振动特性进行了实验测试。经对比分析, 结果表明,仿真模型精度达到87%, 仿真结果准确。这为进一步深入研究振动特性对摩擦副使用性能和寿命, 具有理论研究和工程设计指导意义。

摩擦片；振动特性；实验测试；高线速

车辆传动变速离合器摩擦副在高线速情况下，在结合分离过程中会产生热变形，从而引起轴向振动，严重影响摩擦元件及相关零部件的使用性能[1-3]。摩擦副热变形及其产生的轴向振动是车辆综合传动装置离合器设计所要面对的基础性问题。因此，研究高线速摩擦副摩滑过程中的轴向振动特性，提出有效的振动控制方法，对提高摩擦副使用寿命，具有重要的理论价值和工程设计指导意义。在摩擦振动研究方面国内外学者做了很多工作，但基本以干式制动摩擦为研究对象[4-6]，未考虑湿式摩擦副高线速摩滑产生的微观热变形所引起的振动问题。文献[7]进行了热弹非稳定性分析，提出了一种振动诊断方法，但未对微观热变形量进行接触特性分析，缺少热变形量的量化指标，没有实验验证依据。

本文从微观力学角度出发，建立热弹变形微观法向单元接触数学模型，并通过微观和宏观间的转化关系，获得摩擦副宏观法向弹性接触数学模型；引入KV模型，增加黏弹性接触微分算子，构建包含有应力和应变关系的黏弹性接触属性的数学模型，得到摩擦副黏弹性接触数学模型，采用归一化方法，建立轴向振动数学模型，并对振动特性进行仿真，最后对不同转速、不同润滑油量条件下的振动特性进行实验测试，验证仿真模型。

1 摩滑过程轴向振动数学模型

1.1 轴向动力学模型

车辆传动系统湿式离合器摩擦副由摩擦片和对偶钢片交替接触组合而成，整个离合器摩擦副轴向振动模型可分解为多个摩擦副子振动模型[8-9]，即模型是由多个轴向子振动模型串联组成，如图1所示。每一个子振动模型相互间都是通过力矩M和轴向力Fn关联。每个子模型仅包含有一个摩擦副，根据动力学和接触力学原理，子模型的动力学模型(见图2)。 图2中函数Fnc为两接触面间的法向接触力，该接触力是由法向弹性接触力和法向黏弹性接触力标量和组成；Fkn为结构刚度弹性力；Fc为阻尼力。

根据实验台实际工况条件，将模型初始边界条件设为包含一个初始为静态的环形对偶钢片，和一个带有固定角速度的摩擦片。为了能使仿真结果与实验结果具有可比较性，即保证仿真和实验测试边界条件的一致性，设对偶钢片在轴向加压后的摩滑过程中，将不能绕中心线进行旋转，只能在法向位置方向进行微位移振动，而摩擦片在滑摩过程中，则可以进行旋转，并且在轴向加压过程中，还可以沿着轴线(法向方向)进行微位移振动。在轴向压力作用下，当摩擦副完全结合后，模型中的摩擦片将固定在法向位置，不能绕中心线进行旋转。

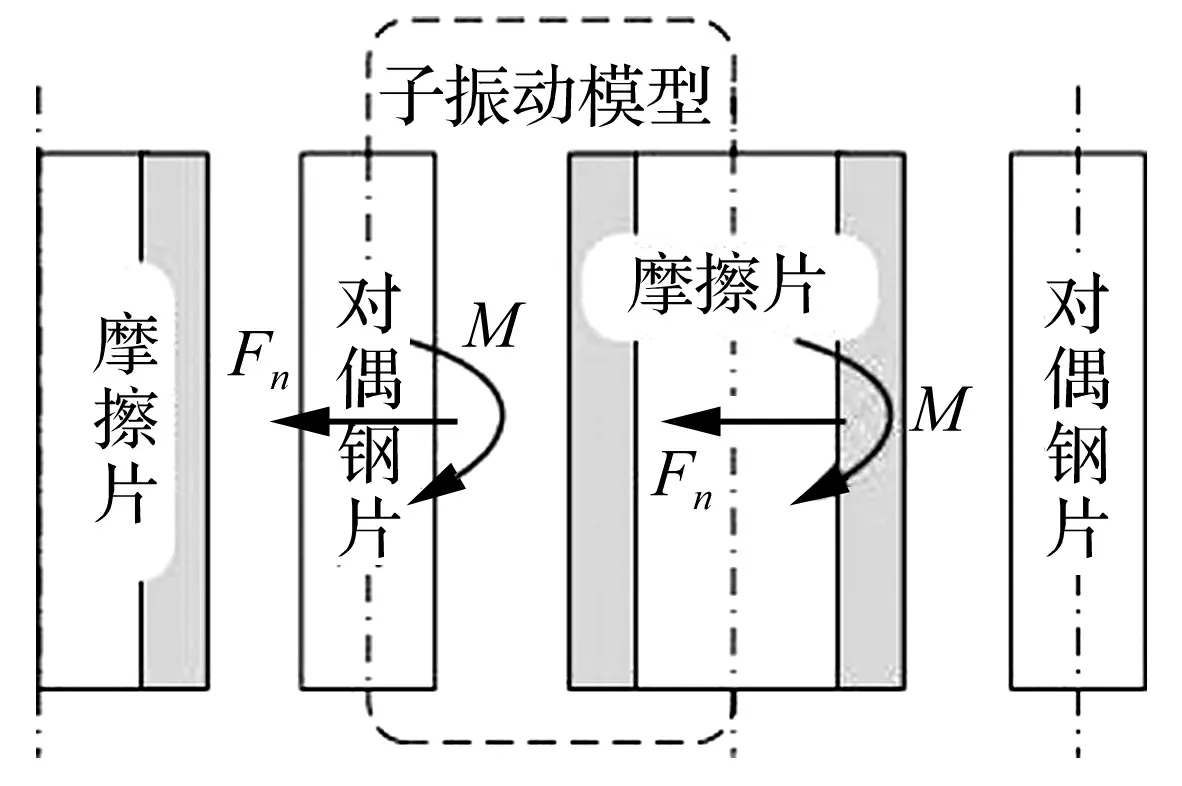
图1 轴向振动子模型Fig.1 Axial vibration sub-model

图2 动力学模型Fig.2 Dynamic model

图2中模型动力学方程为

(1)

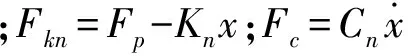
1.2 微凸体法向接触模型

对于高线速接触的摩擦副表面，在高温高压作用下，将产生局部热点现象，其热弹变形结构表现为微凸体形状[10-11]，因此接触模型为热变形微凸体接触形式，摩擦副相互作用接触模型如图3所示。图3中S1和S2分别为接触的摩擦表面;h0为初始间隙;β1和β2分别为两微凸体峰值处曲率半径;z1和z2为微凸体高度。

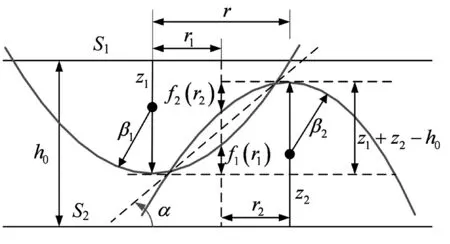
图3 微凸体接触模型Fig.3 Micro-bulges contact model

图3中两表面微凸体进行接触并相互作用，从接触区域中心沿接触法线向两表面方向，Hertz接触力与表平面为非正交，与法向成α角，根据Hertz接触力公式，微凸体接触力表达式为

(2)

式中:E为混合弹性模量;β(r)为混合曲率半径;w为沿着接触法线从中心到表面在接触区域内的干涉量;r为相互接触的两微凸体在切向方向的偏移距离。因此，当r为0时，微凸体是沿法线从中心到平面处于相互干涉;当r不为0时，则沿着一个斜线处于干涉，当两微凸体曲线处于相切状态时;当r为最大值时，接触区干涉力学模型如图4所示。

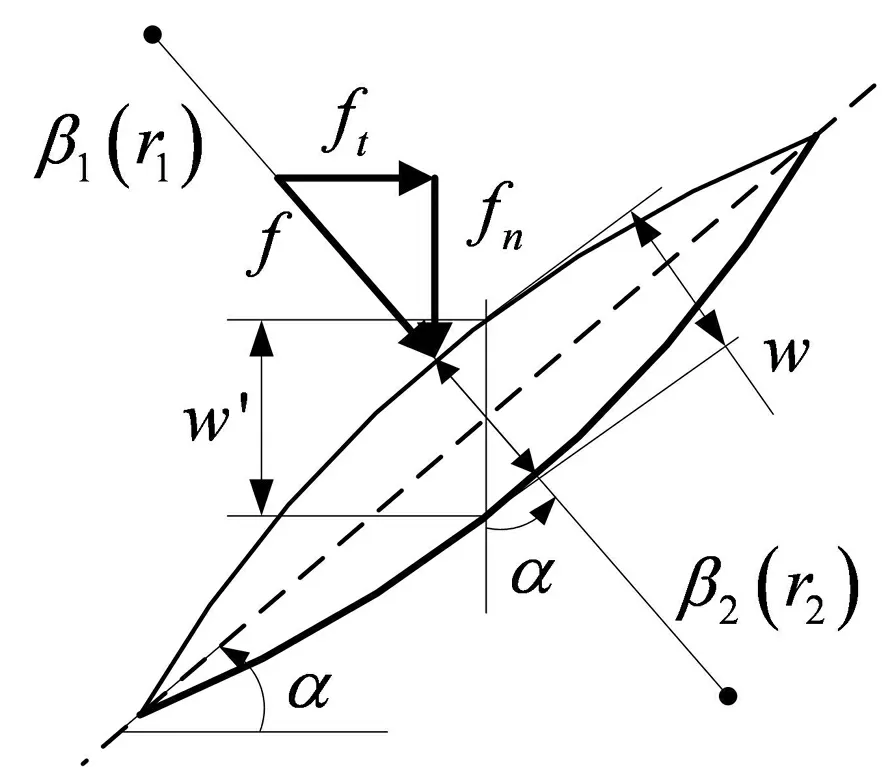
图4 干涉力学模型Fig.4 Interference mechanical model

在图4模型中，干涉量类似于等效曲率[12]，发生在接触位置的中心上，大致在未变形微凸体十字交叉处的中线上。经计算推导，微凸体曲线任意点处的曲率半径和干涉量可表达为

(3)

(4)

式(2)中微凸体接触力被定义为沿着法向方向延伸到接触区，主要包含法向和切向单元。令z=z1+z2，表示微凸体高度之和。将式(3)和式(4)代入式(2)，则微凸体法向单元接触力fn可表示为

(5)

1.3 法向弹性接触数学模型

对于摩擦副在摩滑过程中的轴向振动，变接触力dFns中所有的法向单元都可以看成是并行的。因此，可通过数理统计平均值方法进行几何相加，来获得一个摩擦表面对另一个摩擦表面的法向合力。设两表面微凸体高度总和服从高斯分布[13]，即z～N(h,σ)以标准差σ作为归一化参数，将全部参数进行归一化，则摩擦副整个表面法向弹性接触力分布函数Fne为

(6)

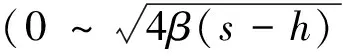
(7)

1.4 法向黏弹性接触数学模型

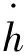
Fnv=Fnvh+Fnvr

(8)

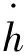
(9)

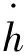
(10)

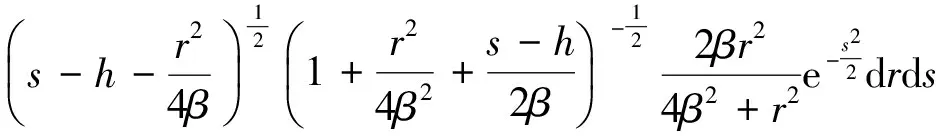
2 轴向振动特性仿真

根据前面推导的公式，将各相关参数仿真结果代入动力学方程式(1)中，即为摩擦副在热变形条件下的摩滑过程非线性轴向振动微分方程。在国际单位制下，微分方程中各物理量之间的数量级相差很大，如刚度系数的数量级为107～109，阻力系数数量级为102～104，而振动响应位移的数量级则在毫米级，这使得对方程求解计算带来很大困难。因此，要对微分方程进行归一化处理。此外，由于强非线性微分方程，一般都要用数值方法求解，在进行求解时，如果同一方程中各量的数量级相差很大，则使误差控制值和步长值难以选择。因此，在对摩擦副振动特性仿真时，依然采用前面所述的归一化方法对振动方程进行求解计算。将法向弹性接触特性、黏弹性接触特性(包含摩擦副间隙变化率和摩滑速率相关的两种特性)、预载荷特性代入动力学方程，则摩擦片摩滑过程振动方程转换为

(12)

式中:ω0为圆频率;ζ为阻尼比;fi(i=p,ne,nvh,nvr)为归一化后的各接触力或载荷。对式(12)在摩擦副一次结合过程中，采用龙格-库塔法，进行摩擦片振动特性数值仿真计算，在无量纲参数h=1，β=100时的仿真结果如图5～图8所示。

从图5和图6中的仿真结果可看出:在受迫力作用下，摩擦副进行往复震荡振动，并在阻尼作用下，系统逐渐趋于稳定，系统收敛于初始原点，其振动幅值在±1 mm之间。

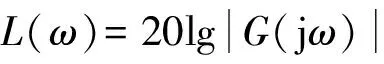
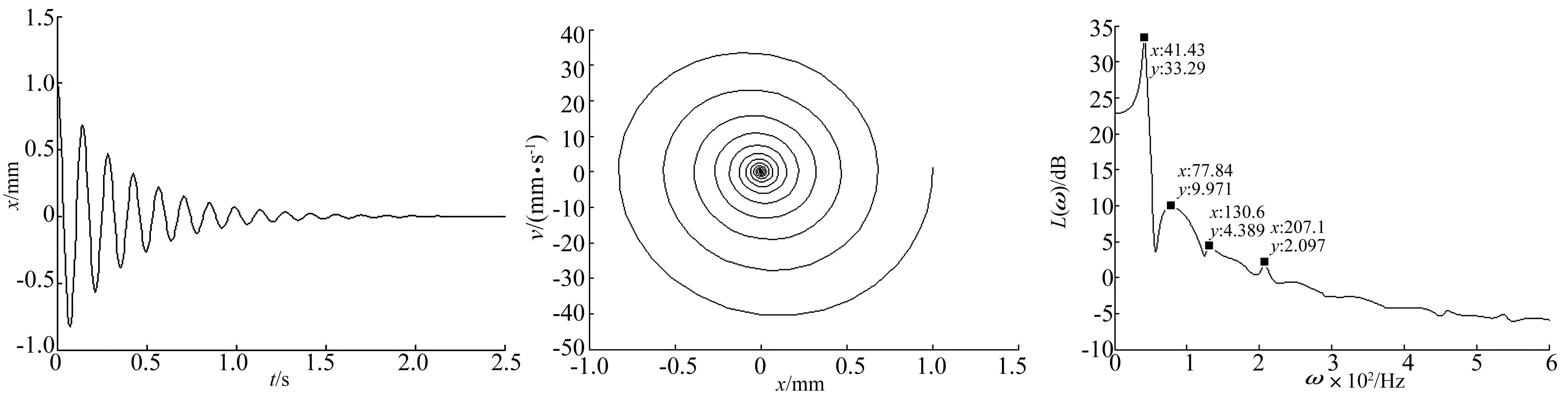
图5 时域仿真曲线Fig．5Timesimulationcurves图6 相平面图Fig．6Phase⁃planediagram图7 幅频特性Fig．7Amplitudefrequencycharacteristics

图8 Bode图Fig.8 Bode curves

由图8可知，主振峰值在40～50 Hz，在低频范围内，幅值基本保持为一个恒值，相位角基本为0°；在高频范围内，每增加一个10倍频程，幅值下降约42 dB，相位角基本保持在-180°附近。

3 轴向振动实验测试

实验测试是在中国北方车辆研究所车辆传动重点实验室离合器实验台上进行，实验为对某型重载车辆405湿式变速离合器摩擦片进行在不同工况下的结合/分离过程中的轴向振动测试。实验台动力端及加载端为电机控制单元，最大功率为315 kW。实验采用左端为轴向加压载荷端，与离合器外毂(内齿与对偶钢片啮合)保持同步运动，右端为旋转动力端，最高可实现4 000 r/min，与内毂(外齿与摩擦片啮合)保持同步转速。实验台布置如图9所示。

图9 离合器实验台Fig.9 Clutch test

主要测试仪器：加速度传感器ULT2754，灵敏度420 mV/g，频率响应1 000 Hz；热电偶SP602G，精度±0.25%；转速转矩传感器FLFM1iS，扭矩精度±0.1%，转速脉冲数1 024 ppr；伺服作动器内差动变压位移传感器ATOS CK-LVDT，精度0.001%，分辨率5 μm。实验测试条件需满足线速度≥70 m/s的指标要求，因此，测试中转速在3 000 r/min时开始采集数据。 3 000 r/min时结合分离过程实验测试结果如图10～图12所示。

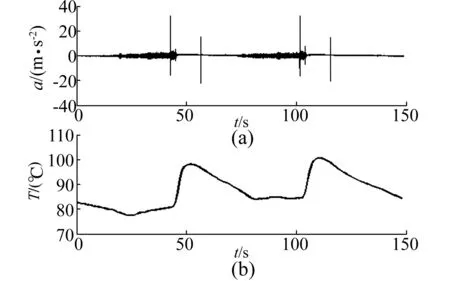
图10 两次结合分离过程测试(3 000 r/min)Fig.10 Twice sliding test(3 000 r/min)

由图11～12中可知，3 000 r/min时的振幅在±1.5 mm之间，振动能量基本集中在前两阶共振频率内，最

大振幅发生在46.46 Hz处。经PSD计算，前两阶共振能量占总能量的87%，且第2阶频率是第1阶频率的1.89倍，第三阶是第1阶的3.11倍，第4阶是第1阶的5.1倍。3 100～3 400 r/min时测试结果经数据处理后得到的幅频特性如图13～16所示。

由图13～16幅频特性可知，摩擦副为3 100～3 400 r/min时，振动特性与3 000 r/min时的特性基本相同，振动能量基本集中在前两阶共振频率内。经PSD计算，前两阶能量占总能量的86%～88%，最大振幅频率为38.9～47.71 Hz，频响为32～41 dB。对于倍频数，将不同转速下测试获得的倍频数与谐振阶数用曲线表示，如图17所示。

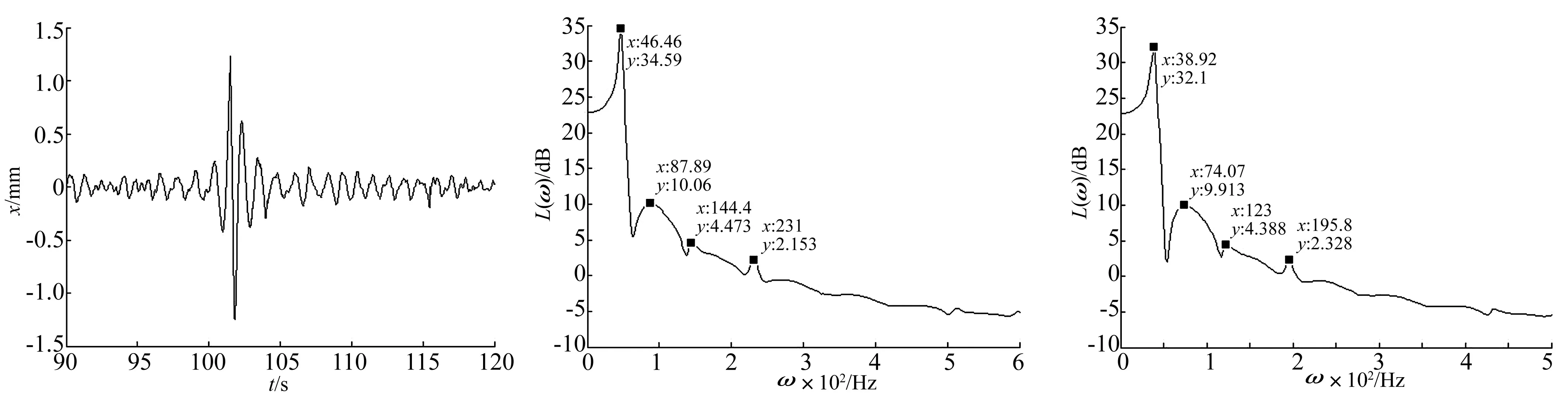
图11 时域振动曲线Fig．11Timecurve(3000r/min)图12 幅频特性(3000r/min)Fig．12Amplitudefrequencycharacteristics(3000r/min)图13 幅频特性(3100r/min)Fig．13Amplitudefrequencycharacteristics(3100r/min)

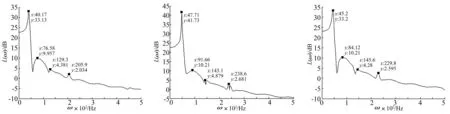
图14 幅频特性(3200r/min)Fig．14Amplitudefrequencycharacteristics(3200r/min)图15 幅频特性(3300r/min)Fig．15Amplitudefrequencycharacteristics(3300r/min)图16 幅频特性(3400r/min)Fig．16Amplitudefrequencycharacteristics(3400r/min)

由图17可知，不同转速下各阶谐振频率的倍频数基本相同，最大倍频偏差出现在3阶谐振，变化率为7.3%，2阶谐振最大变化率为3.2%， 4阶倍频数变化率为2.4%。这说明摩擦副在摩滑过程中产生的轴向振动，不论转速多少，共振发生的各阶谐次必然发生在这些范围内，因此只要确定了主谐次的频率，其它各阶次谐振频率范围也基本能够确定。将不同转速下的幅频特性在谐振点处数值用曲线表示，如图18～19所示。

由图18可知，不同转速下的各阶谐振频率基本都是在各阶共振频带范围内，但随着阶数的升高，偏差逐渐增大，其1阶最大偏差为8.79 Hz，2阶最大偏差17.59 Hz，3阶22.6 Hz，4阶35.2 Hz。在图19中，响应幅值则是随着谐振阶数的升高，偏差逐渐减小，其最大偏差发生在1阶，偏差为9.63 dB，2阶0.297 dB，3阶0.599 dB，4阶0.647 dB。

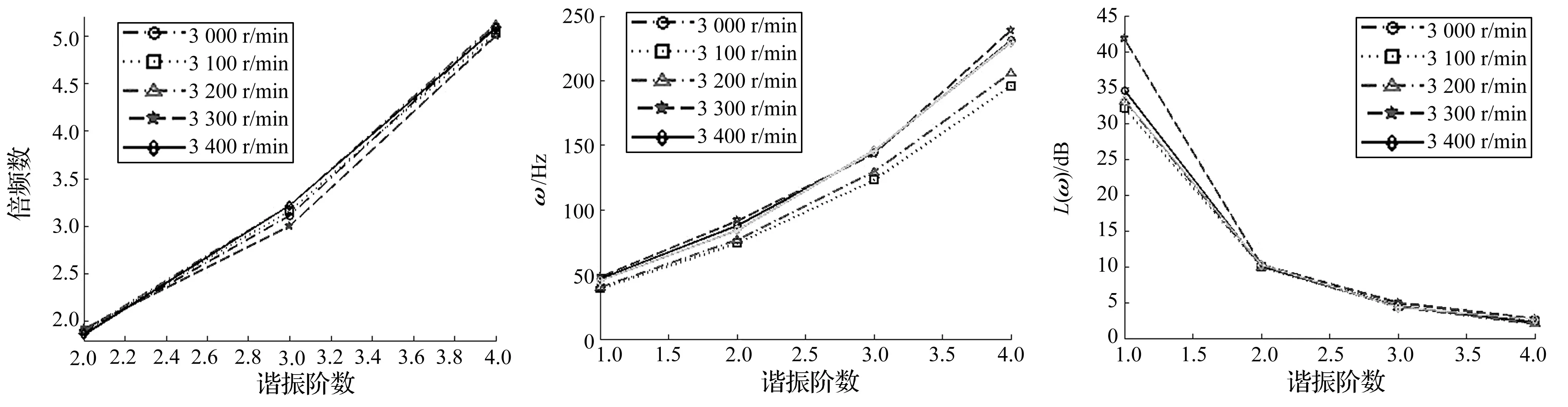
图17 不同转速下的倍频Fig．17Frequencymultiplicationofvariousspeed图18 不同转速下的谐振频率Fig．18Resonancefrequencyofvariousspeed图19 不同转速下的幅频响应Fig．19Amplitudefrequencyresponseofvariousspeed

4 模型精度验证

将仿真获得的倍频数结果与实验测试数据进行对比，对比结果如图20所示。

由图20可知，仿真数值全部落在了实验测试范围内，说明仿真结果可靠，仿真所用数学模型准确。将仿真谐振频率和幅频响应与实验测试数值进行对比，其结果如图21～图22所示。

由图21和图22可知，仿真值全部落在了实验测试范围内，进一步证明仿真模型可靠。对实验与仿真各阶偏差率分别进行计算，取偏差率最大值，结果表明：仿真模型精度为87%。

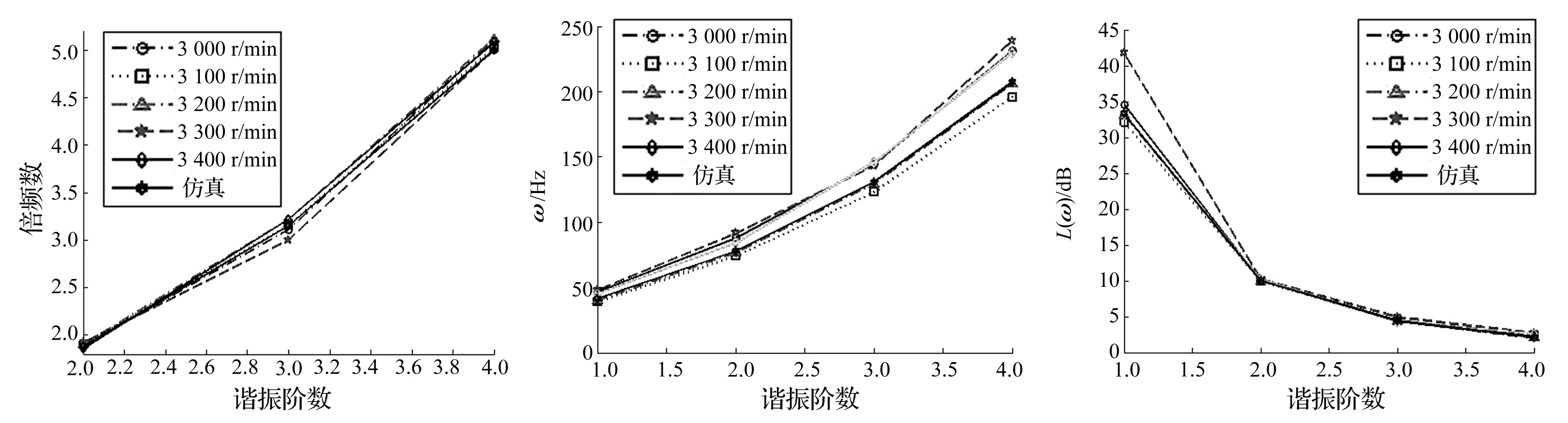
图20 不同转速下的倍频Fig．20Frequencymultiplicationofvariousspeed图21 不同转速下的谐振频率Fig．21Resonancefrequencyofvariousspeed图22 不同转速下的幅频响应Fig．22Amplitudefrequencyresponseofvariousspeed

5 结 论

根据对高线速摩擦副摩滑过程的振动特性进行的理论和实验测试分析，可以得到以下结论

(1)摩擦副在摩滑过程中，振动能量主要集中在谐振的前两阶，即100 Hz以内，且前两阶共振能量约占总能量的87%。

(2)最大振幅发生的频率在38.9～47.71 Hz，频响为32～41 dB，随着频率的增加，每增加一个10倍频程，幅值下降约42 dB。

(3)各阶倍频程分别为1.89、3.11和5.1，最大误差率不超过7.3%。

对仿真结果与实验测试结果对比，验证仿真模型精度为87%，表明仿真模型可靠，仿真结果准确。

[ 1 ] 闫清东, 张连第, 赵毓芹, 等.坦克构造与设计[M].北京: 北京理工大学出版社,2012.

[ 2 ] 郑慕侨.坦克装甲车辆[M]. 北京:北京理工大学出版社,2003.

[ 3 ] LI Jie, WANG Xiaoyan, WANG Zhiyong. Study on interaction theory of thermal distortion friction pairs and effect on friction coefficient [J]. Applied Mechanics and Materials,2014, 713/714/715: 223-227.

[ 4 ] 刘富豪,蒋汉军,朱龙英.汽车盘式制动器稳定性及非线性动力学分析[J]. 振动工程学报,2014,27(6): 907-914. LIU Fuhao, JIANG Hanjun, ZHU Longying.Stability and nonlinear dynamics analysis of automotive disc brake[J]. Journal of Vibration Engineering,2014,27(6): 907-914.

[ 5 ] 孟宪皆, 吴光强. 汽车制动盘和摩擦片振动的数值解[J].江苏大学学报,2011,32(3): 291-295. MENG Xianjie, WU Guangqiang.Numerical solution for vibration behavior of automotive brake disc and pads[J]. Journal of Jiangsu University,2011,32(3): 291-295.

[ 6 ] 肖会芳，杨荃，邵毅敏，等.润滑状态下线接触滑动粗糙界面的动摩擦特性研究[J].振动与冲击,2016,35 (1): 188-194. XIAO Huifang,YANG Quan,SHAO Yimin,et al.Dynamic friction characteristics of sliding rough interfaces in line contact under labrication[J].Journal of Vibration and Shock,2016,35 (1): 188-194.

[ 7 ] 陈漫,李和言,马彪,等. 多片离合器早期故障生成机理及振动诊断方法[J].机械工程学报,2015,51(1):117-122. CHEN Man, LI Heyan, MA Biao, et al.Initial malfunction generating mechanism and vibration diagnosis method on multi-plate clutch[J]. Journal of Mechanical Engineering, 2015,51(1): 117-122.

[ 8 ] ZAGRODZKI P, TRUNCONE S. Generation of hot spots in a wet multidisk clutch during short-term engagement[J]. Wear, 2003,254(5/6):474-491.

[ 9 ] ZAGRODZKI P, LAM K, BAHKALI E, et al. Non-linear transient behavior of a sliding system with frictionally excited thermoelastic instability [J]. ASME Journal of Tribology,2001,123(4):699-708.

[10] FARHANG K, LIM A L. A non-phenomenological account of friction-vibration interaction in rotary systems [J]. Journal of Tribology,2006, 128(1):103-112.

[11] FARHANG K, OZCAN S, FILIP P. The effect of wear groove on vibration and noise of aircraft brakes: theoretical and experimental evidence [J]. SAE International Journal of Aviation Industry Development Research,2008, 1(1):1223-1229.

[12] MCCOOL J L. Extending the capability of the greenwood williamson microcontact model [J]. ASME Journal of Tribology, 2000,122(3):496-502.

[13] BENGISU M, AKAY A. Stick-slip oscillations: dynamics of friction and surface roughness [J]. Journal of Acoustics and Sociology,1999,105(1): 194-205.

[14] CHENG W,FARHANG K. A contact model of nominally flat rough surfaces based on a visco-elasto-adhesive interaction [J]. Journal of Tribology,2009, 131(10):504-509.

[15] GREENWOOD J, WILLIAMSON J. Contact of nominally flat surfaces[C]//London: Proceedings of Royal Society, 1996:300-306.

[16] POLYCARPOU A, ETSION I. Analytical approximations in modeling contacting rough surfaces [J]. ASME Journal of Tribology,1999, 121(2):234-239.

[17] KOMVOPOULOS K, YANG W. Three-dimensional elastic-plastic fractal analysis of surface adhesion in micro-electromechanical systems [J]. ASME Journal of Tribology,1998, 120(4):808-812.

Axial vibration characteristics of friction disks of clutch on sliding

WANGXiaoyan2,LIJie1,3,ZHANGZhikai1,WANGZhiyong1,XINGQingkun1

(1. Science and Technology on Vehicle Transmission Laboratory, China North Vehicle Research Institute, Beijing 100072, China； 2.School of Information, Beijing Wuzi University, Beijing 101149, China; 3.School of Mechanical-electronic and Automobile Engineering,Beijing University of Civil Engineering and Architecture, Beijing 100044,China)

By analyzing friction disk surface structural characteristics and using theory of contact mechanics, a micro-normal unit contact mathematic model of thermal distortion friction pairs was built. Using mathematic statistics and normalization, the micro-model could be transferred to macro-mathematic model, and then the normal elastic contact characteristics of friction pairs could be obtained. When the Kelvin-Voigt (KV) model was inputted into elastic contact characteristics, viscoelastic contact differential operator was included in the equation, and viscoelastic contact mathematic model that included the relation of stress to strain was built. So colligating above all the simulation results, an axial vibration mathematic model was built, and the vibration characteristics was obtained by simulation. For verifying simulation results, axial vibration experiment of friction pairs of clutch was tested on conditions of various rotational speeds. The contrasted results show that model precision is 87%, and the simulation results are correct. This is significant in theory and engineering design, and promotes studying deeply on vibration characteristics to advance friction pairs serviceability and life.

friction disks; vibration characteristics; testing; high line speed

国家自然科学基金(11201482;51675494)

2015-08-07 修改稿收到日期：2016-02-26

王晓燕 女，博士，讲师，1980年生

李杰 男，博士，副研究员，1977年生

TJ8；U463

A

10.13465/j.cnki.jvs.2017.04.013