基于拉伸振动精确化理论求解含孔厚板弹性波散射问题

周传平, 胡 超

(1.杭州电子科技大学 机械工程学院，杭州 310018； 2.扬州大学 建筑科学与工程学院，扬州 225127)

基于拉伸振动精确化理论求解含孔厚板弹性波散射问题

周传平1, 胡 超2

(1.杭州电子科技大学 机械工程学院，杭州 310018； 2.扬州大学 建筑科学与工程学院，扬州 225127)

针对采用弹性力学平面问题求解波动/振动时常产生较大误差的问题，基于厚板拉伸振动精确化方程，采用复变函数方法对含孔平板中弹性波散射与动应力集中问题进行了研究。利用正交函数展开的方法将待解的问题归结为对一组无穷代数方程组的求解。给出了含椭圆孔厚板拉压弹性波散射与动应力集中的数值结果。研究结果表明：动应力集中系数与分布取决于入射波数、平板厚度、椭圆偏心率等无量纲化参数。

平板拉伸振动精确化方程；厚壁动力学；弹性波散射与动应力集中；复变函数法；剪应力一阶矩

在航空航天、船舶、土木建筑和机械工程中，受拉伸作用的平板结构经常用铆钉或螺栓连接，普遍存在大量圆孔。由于平板结构几何上的不连续，在开孔附近将会出现应力集中现象。应力集中将会降低结构的承载能力和减少结构的使用寿命，是工程上经常遇到的问题。因此，长期以来人们对拉压平板开孔静、动应力集中问题进行了广泛的研究[1-7]。

对静应力集中问题，KIRSCH[8]按二维弹性力学方程求解了在均匀纵向拉力作用下平板中圆孔周围的应力集中。而对拉压平板考虑动应力集中的工程设计，现多借鉴弹性力学平面问题分析求解，例如二维区域弹性波散射与动应力集中的结果。由于有限厚度结构中承载圆孔的附近会由于应力集中产生强烈的三维效应区。三维效应区和结构的相对厚度紧密相关，很大程度上控制着结构的断裂、疲劳等力学特性。显然，利用平面问题的二维模型求解应力集中问题与平板实际结构特点有差异。随着现代科学技术的发展，工程结构设计趋于轻型化，而实现轻型化的途径是采用先进材料和完善结构设计理论。然而，按三维问题求解时将会遇到极大的数学困难，因此，该问题一直没有很好解决。

直到目前，基于平板拉伸振动支配方程分析求解非圆形孔动应力集中的工作鲜见于文献报道。本文将基于文献[7]给出的厚板拉伸振动精确化方程，对含孔平板中弹性波散射与动应力集中问题进行研究，并给出可供工程应用的分析方法和数值结果。

1 平板拉伸波动方程及其求解

根据文献[7]平板拉伸自由振动的精确化方程为

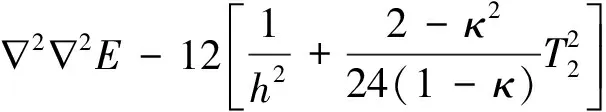
(1a)

(1c)

不失一般性，研究问题的谐和振动解，设

(2)

式中:ω是平板拉伸振动的圆频率；i是虚数单位，i2=-1。

在以下分析中略去时间因子和广义位移函数上的符号～。将式(2)代入到式(1)可得方程

(3a)

(3b)

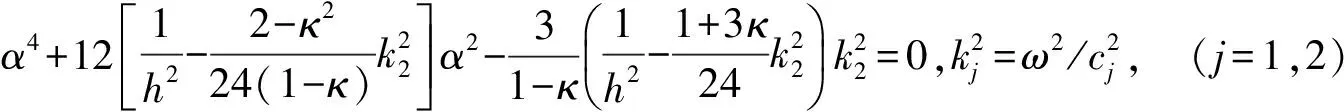
基于平板拉伸精确化理论，平板结构中广义内力的表达式为[8]

(4)

由于剪应力Qx(零阶矩)边界条件自动满足，因此需要补充一个考虑剪应力一阶消失矩的广义内力，其表达式为

(5)

采用复变函数法，在求解平板中任意形状开孔附近的动应力集中问题时，使用保角映射法[9]，将ζ平面上非圆孔洞边界L的外域(内域)映射成η平面上的边界S的单位圆的外域(内域)。映射函数具有如下形式

ζ=Ω(η)=cη+Φ(η)

(6)

式中:Φ(η)为全纯函数。

在极坐标系(r,β)中，式(6)可以写成

Nr+Nβ=Nx+Ny

(7a)

Nβ-Nr+2iNrβ=(Ny-Nx+2iNxy)exp(2iβ)

(7b)

MQr-iMQβ=(MQx-iMQy)exp(iβ)

(7c)

(8a)

(8b)

(8c)

平板拉伸振动方程(3)描述的散射波一般解可写为

(9a)

(9c)

式中:δj(j=1,2)是位移势函数的比例系数，

2 入射波的激发与总波场

设在平板结构中有一拉伸波沿x轴方向传播，其表达式为

E(i)=E0eiα1x

(10a)

F(i)=δ1E(i)

(10b)

f(i)=0

(10c)

式中:E0是入射波沿x轴方向广义位移的幅值。

平板中拉压弹性波总波场可描述为

E=E(i)+E(s)

(11a)

F=F(i)+F(s)

(11b)

f=f(i)+f(s)

(11c)

3 满足开孔边界条件确定模式系数

在η平面上，设平板结构拉压振动时开孔为自由边界条件，厚板理论可以满足3个边界条件

(12)

式中:a为平板开孔的半径。

将式(11)代入到开孔边界条件式(12)中，可以构成决定A1n,A2n,Bn的无穷代数方程组：

(13)

(14)

式中：

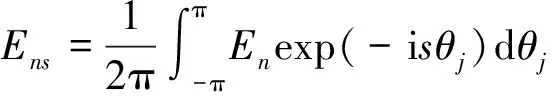
用e-isθ乘以方程(14)的两端，利用函数系的正交性可得

开孔边界处动应力集中系数可描述为

(15)

式中，入射波的表达式为

(16)

开孔边界处散射波的表达式为

(17)

4 数值算例

对于平板中含有一个长短半轴分别为a和b的椭圆孔，取映射函数为

(18)

式中:r0=(a+b)/2，c=(a-b)/(a+b)。

本文根据含任意形开孔平板结构拉伸振动的精确化理论及其相应的分析计算公式，编制了计算程序，并绘出了动应力分布曲线。在作数值计算时，Poisson比取为ν=0.3，无量纲波数为α1a=0.1～5.0。

(a) α1a=0．1，a/h=0．1，a/b=3/4(b) α1a=1．0，a/h=0．1，a/b=3/4(c) α1a=1．0，a/h=5．0，a/b=3/4(d) α1a=5．0，a/h=5．0，a/b=3/4图1 拉伸平板孔边动应力分布Fig．1Dynamicstressinstretchingplates

(a) α1a=0．1，a/h=0．1，a/b=4/3(b) α1a=1．0，a/h=0．1，a/b=4/3(c) α1a=1．0，a/h=5．0，a/b=4/3(d) α1a=5．0，a/h=5．0，a/b=4/3图2 拉伸平板孔边动应力分布Fig．2Dynamicstressinstretchingplates

图3是基于平板拉伸的精确化理论分析计算得到的含椭圆孔厚板动应力集中系数随无量纲波数α1a的变化曲线。

图3 不同板厚情况下含椭圆孔厚板动应力集中系数随波数变化曲线(ν=0.3,θ=π/2,a/b=3/4)Fig.3 Dynamic stress in plates vs dimensionless wave numbers for different thickness

5 结 论

本文基于文献[7]的平板拉伸振动精确化方程，采用刘氏复变函数方法，对平板开孔弹性波散射与动应力集中问题进行了研究。为说明问题，文中就平板含椭圆形开孔情况下的动应力集中问题进行了数值模拟。研究结果表明：

(1)动应力集中系数与分布取决于入射波数、平板厚度和椭圆的偏心率等无量纲化参数。

(2)当入射波波数变较大时，动应力集中系数最大值趋于单位一。从物理上讲，这意味着频率非常高时，孔的边界如同一个平面边界，这充分反映了高频动态应力集中的特点。

(3)在中高频和薄板的情况下，在θ=π/2处动应力集中系数未能取得最大值，甚至出现负应力。

根据文献[7]可知，平板拉伸振动精确化方程是在没有采用任何工程假设情况下得到的，其动力学方程是较精确的。基于此振动精确化方程， 采用复变函数

方法和保角映射法配以适当的映射函数可精确求解平板任意形开孔的动应力集中问题。该研究方法的特点是有规范的求解方式，因此本文方法与数值计算结果可望能在工程厚壁结构的动力学分析与强度设计中得到应用。

[ 1 ] SAVIN G. N.著, 卢鼎霍译. 孔附近的应力集中[M]. 北京: 科学出版社, 1965.

[ 2 ] ERINGEN A C, SUHUBI E S. Elastodynamics,volume II linear theory[M]. New York, San Francisco, London: Academic Press, 1975.

[ 3 ] LIU D K, HU C. Scattering of flexural wave and dynamic stress concentration in Mindlin thick plates[J]. Acta Mechanica Sinica, 1996, 12(2): 169-185.

[ 4 ] MINDLIN R D. Influence of rotatory inertia and shear on flexural motionsof isotropic elastic plates[J]. ASME Journal of Applied Mechanics, 1951, 18: 31-36.

[ 5 ] PAO Y H, MOW C C. Diffraction of elastic waves and dynamic stress concentrations[M]. New York: Crane and Russak, 1973. 230-231.

[ 6 ] 胡超, MA Fai, 马兴瑞,等. 平板弯曲自由振动的精确化动力学方程及其分析[J]. 中国科学, G辑, 物理、力学、天文学, 2011, 41(6):781-790. HU Chao, MA F, MA Xingrui, et al. Refined dynamic equations of the plate bending without any assumptions[J]. Sci Sin Phys Mech Astron, 2011, 41(6):781-790.

[ 7 ] 胡超, MA Fai, 马兴瑞,等. 厚板弯曲与拉伸振动精化理论及其求解新途径[J]. 中国科学, G辑, 物理、力学、天文学, 2012, 42(5):522-530. HU Chao, MA F, MA Xingrui, et al. Refined dynamic theory of thick plates in extension-bending and its new formulism[J]. Sci Sin-Phys Mech Astron, 2012, 42(5): 522-530.

[ 8 ] SAADA A S. Elasticity theory and applications[M]. Fort Lauderdale: J. Ross Pub, 2009.

[ 9 ] MUSKHELISHVILI N I. Certain fundamental problems of the mathematical theory of elasticity[M]. Moscow: Izd-vo Nauka, 1966.

[10] ABRAMOWITZ M, STEGUN I A. Handbook of mathematical functions with formulas, graphs, and mathematical tables[M]. New York:Dover publications, 1964.

Elastic wave scattering in thick plates with a hole based on thick plates’ longitudinal vibration equation

ZHOU Chuanping1, HU Chao2

(1. School of Mechanical Engineering, Hangzhou Dianzi University, Hangzhou 300018, China;2. College of Civil Science and Engineering, Yangzhou University, Yangzhou 225127, China)

Based on longitudinal vibration equation of thick plates, using the complex functions and mapping method, elastic wave scattering and dynamic stress concentrations in thick plates with a hole were studied. Applying the orthogonal function expansion method, the problem to be solved was converted into solving a set of infinite algebraic equations. As an example, the numerical results for tension-compression elastic wave scattering and dynamic stress concentration factors in thick plates with an elliptic hole were computed. The results indicated that some parameters, such as, incident wave number, thickness of plates and elliptic eccentricity ratio have great effects on dynamic stress distributions and dynamic stress concentratuion factors of thick plates with a hole.

longitudinal vibration equation of thick plates; dynamics of thick walled structures; elastic wave scattering and dynamic stress concentrations; complex functions method; first moment of shear stresses

国家自然科学基金项目(51378451)

2015-11-02 修改稿收到日期：2016-01-23

周传平 男，博士，讲师，1985年生

胡超 男，博士，教授，1961年生

O347.4；TU311.3

A

10.13465/j.cnki.jvs.2017.03.035