基于奇异值分解的摩擦振动吸引子特征参数提取方法

柳 霆， 李国宾， 魏海军， 穆 雪， 邢鹏飞

(1.大连海事大学 轮机工程学院，大连 116026； 2.上海海事大学 商船学院，上海 200135；3.大连中远国际货运有限公司，大连 116001)

基于奇异值分解的摩擦振动吸引子特征参数提取方法

柳 霆1， 李国宾1， 魏海军2， 穆 雪3， 邢鹏飞1

(1.大连海事大学 轮机工程学院，大连 116026； 2.上海海事大学 商船学院，上海 200135；3.大连中远国际货运有限公司，大连 116001)

为定量研究摩擦副磨损过程中摩擦振动吸引子的变化，根据相空间重构理论，应用C-C法重构摩擦振动吸引子相空间矩阵，对相空间矩阵进行奇异值分解，通过奇异值构建矩阵奇异值特征向量，定义其特征参数为摩擦振动吸引子特征参数K，并分析特征参数K在摩擦副磨合磨损过程中的变化规律。结果表明：磨合开始，摩擦振动能量较低，吸引子体积较小，K值亦较小，为9.36；随磨合进行，摩擦振动能量逐渐增加，吸引子体积逐渐增大，K值亦逐渐增大；43 min后，摩擦振动能量保持平稳，吸引子体积趋于稳定，K值在24.72附近平稳波动。因此，摩擦振动吸引子参数K可用于定量分析磨合过程中摩擦振动能量的变化；K与摩擦因数对磨损阶段的判断一致，进而可用于磨损状态的识别。

摩擦振动；奇异值分解；吸引子；特征参数

摩擦振动是摩擦学系统重要的输出特征信息之一，摩擦振动的非线性行为可反映摩擦副的磨损状态。为此，许多学者应用非线性理论对摩擦振动进行了大量研究。朱华等[1-3]提取了摩擦振动信号Kolmogorov熵、Lyapunov指数、分形维数等非线性特征参数并分析其在摩擦副磨损过程中的变化规律，发现上述非线性特征参数可以实现摩擦副摩擦磨损过程中不同磨损阶段的识别。LI等[4]通过分形理论提取了磨合过程中摩擦振动信号的多重分形特征参数，发现摩擦振动信号的多重分形特征参数可识别摩擦副的磨合磨损和稳定磨损阶段。可见，摩擦振动的非线性特征能够反映摩擦学系统的摩擦学行为，可用于识别摩擦副的磨损状态。

摩擦学系统是一个复杂的非线性动力学系统[5]，从单一的摩擦学行为难以全面认识摩擦学系统的性质，还需多方法、多信息地对磨损过程进行研究。近年来，一些学者在摩擦振动吸引子的研究中发现[6-9]：吸引子相空间轨迹的体积变化反映了摩擦副摩擦磨损过程中磨损能量的变化，可通过能量变化识别摩擦副的磨损状态，为摩擦副磨损状态的识别提供了一条新途径。然而，目前摩擦振动吸引子相空间轨迹的研究还缺乏量化方法，在判断吸引子体积变化时，存在主观性强，细微差异难以区分等问题。为解决定性分析存在的问题，本文应用奇异值分解方法从摩擦振动吸引子相空间矩阵定量地提取摩擦振动吸引子特征参数，研究磨合磨损过程中摩擦振动吸引子特征参数的变化及其与磨损状态的对应关系。

1 摩擦振动吸引子特征参数提取

1.1 相空间重构

本文根据TAKENS定理[10]用 C-C 方法重构摩擦振动吸引子相空间。摩擦振动信号时间序列通过嵌入维数m及时间延迟τ可构造出多维摩擦振动吸引子相空间矩阵X:

式中：N为时间序列长度；Xi为相空间中的矢量。重构摩擦振动吸引子相空间矩阵的关键在于嵌入维数m和时间延迟τ的选取。本文运用C-C方法确定m和τ。

(1)时间序列的关联积分C(m,N,r,t)的计算

C(m,N,r,t)=

(1)

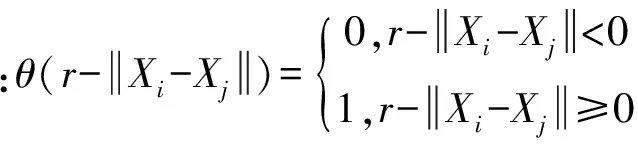
(2)子列的统计量S(m,r,t)的定义

将摩擦振动信号序列分成t个不相交子列，计算t取不大于200的正整数。

S(m,r,t)=

(2)

由于实际时间序列S(m,r,t)≠0，取呈近似均匀分布的S(m,r,t)零点或对所有半径r差别最小的时间点为局部最大时间间隔。

(3)差量ΔS(m,t)的定义

ΔS(m,t)=max{S(m,r,t)}-min{S(m,r,t)}

(3)

S(m,r,t)零点或者ΔS(m,t)最小值为局部最大时间t，τd对应t中的第一个，同时由τd=ττs求取τ。

定义指标函数Scor(t)为：

(4)

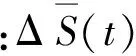
1.2 吸引子特征参数提取

为提取能定量表征摩擦振动能量的特征参数，本文对吸引子相空间矩阵进行矩阵奇异值分解并构建奇异值特征向量，通过奇异值向量模定义摩擦振动吸引子特征参数K，具体方法如下。

1.2.1 矩阵奇异值特征向量的构建

奇异值分解(Singular Value Decomposition，SVD)[11-12]是线性代数中一种重要的矩阵分解方法，利用奇异值可实现对矩阵奇异值特征向量的构建。本文应用SVD法构建摩擦振动吸引子相空间矩阵奇异值特征向量，具体方法如下。

根据SVD定义，对相空间重构的摩擦振动吸引子矩阵X进行奇异值分解，可得到r个非零奇异值(λ1,λ2,…,λr)，r为矩阵X的秩，r=rank(X)。定义矩阵X的奇异值特征向量为Y，其表达式为:

Y=(λ1,λ2,…,λr)

(5)

从式(5)可以看出，奇异值特征向量Y是由矩阵X的非零奇异值构成，奇异值唯一表征了矩阵X的特征，因此，由奇异值构成奇异值特征向量Y亦是如此。

1.2.2 矩阵奇异值特征向量模的计算

根据向量的定义可知，向量的模，即向量的长度，可反映向量的大小。向量的模的计算方法如下:

(6)

1.2.3 吸引子特征参数的定义

摩擦振动吸引子的体积变化反映了摩擦副磨损过程中摩擦振动的能量变化。摩擦振动吸引子是吸引子相空间矩阵的几何表征，奇异值特征向量是吸引子相空间矩阵的唯一表征，奇异值特征向量的模描述了奇异值特征向量大小的变化。因此，矩阵奇异值特征向量的模反映了摩擦振动吸引子的体积大小，即摩擦振动能量的高低，故本文定义摩擦振动吸引子奇异值特征向量的模为摩擦振动吸引子特征参数K，即：

(7)

由摩擦振动吸引子特征参数K的定义可以看出，特征参数K可定量反映摩擦振动吸引子体积的大小，即摩擦振动的能量高低。

2 试验

2.1 试验方法

在CFT-Ⅰ型摩擦磨损试验机(兰州中科凯华)上进行球-盘磨合磨损试验，如图1所示。该试验机可实时测量摩擦因数。球和盘试样由专用夹具固定，盘试样固定于台架上，台架由电机经偏心轮带动以实现往复运动。356A16型ICP三轴加速度传感器(PCB PIEZOTRONICS)固定于盘试样下以测量切向和法向摩擦振动信号，应用PXIe-1071(National Instruments)信号采集系统实现切向与法向摩擦振动信号的采集，每间隔1 min采集一次振动信号，采样频率25.6 kHz，采样间隔6.25 Hz。

2.2 试验条件

选取GCr15和铸铁作为磨合磨损试验摩擦副材料。GCr15为球试样，尺寸Φ3 mm，硬度HV830; 铸铁为下试样，尺寸Φ30 mm×10 mm的盘, 硬度HV300～400，材质为合金铸铁，原始三维表面粗糙度Sa=0.842 μm。试验设定电机转速为500 r/min，折合球-盘间的平均线速度为0.083 m/s。在专用储油盘添加足量的常见船用润滑油CD40(密度0.895 7 g/cm3, 40℃运动黏度139.6 cSt, 100 ℃运动黏度12.5 cSt)实现浸油润滑。球-盘间由专业加工的弹簧施加70 N的试验载荷，即名义接触载荷为12 MPa。为保证试验的可重复性，进行5次磨合磨损试验，每次试验进行60 min，取5次试验平均值作为试验结果。

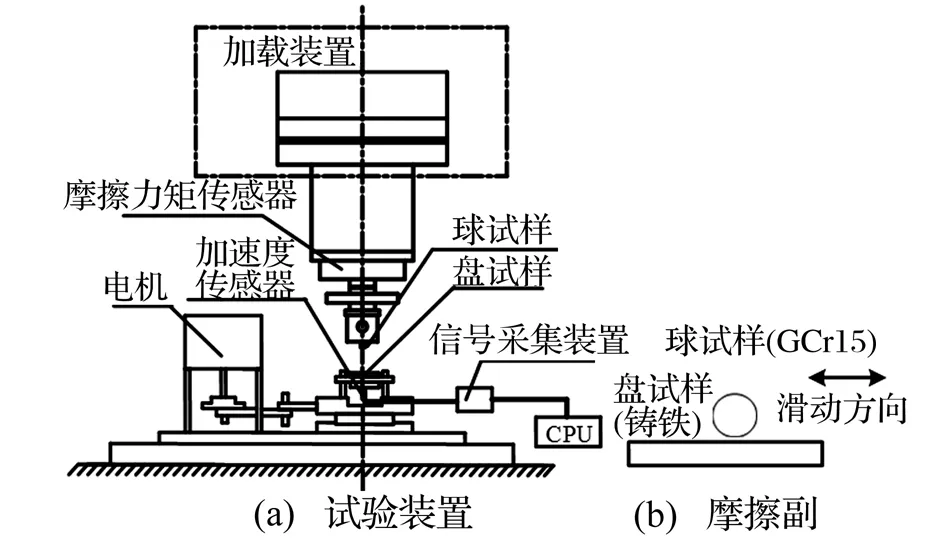
图1 CFT-Ⅰ型摩擦磨损试验机原理图Fig.1 Schematic diagram of CFT-Ⅰwear tester

3 结果与讨论

3.1 摩擦振动吸引子分析

试验采集的摩擦振动信号含有背景噪声，为剔除噪声的影响，根据文献[13]，利用谐波小波包变换对磨合磨损试验中采集的振动信号进行降噪。首先对采集的振动信号进行7层分解，然后根据振动信号频率分布特征，选取38～47频段3 700～4 700 Hz的信号重构摩擦振动信号。图2为试验中某一时刻采集的振动信号和经过降噪后的摩擦振动信号时域波形和频谱图。从图2中可以看出，试验采集的振动信号含有大量背景噪声，而经过谐波小波包变换进行降噪后提取的摩擦振动信号，有效地剔除了噪声影响。相比于原始振动信号，摩擦振动信号主要分布在高频区，且信号比较微弱。

根据混沌理论，对降噪后的摩擦振动信号通过式(1)～式(4)重构摩擦振动吸引子相空间矩阵，并绘制摩擦振动吸引子相空间轨迹图，如图3所示。从图3中可以看出，摩擦副磨合磨损过程中摩擦振动吸引子的体积呈现出由小到大并逐渐平稳的变化过程。摩擦副磨合磨损是能量变化的过程，磨合开始，摩擦副表面光滑且为浸油润滑，激发的摩擦振动能量较低，摩擦振动吸引子体积较小；随着磨合进行，摩擦副相互接触激发的摩擦振动能量逐渐增加，摩擦振动吸引子体积逐渐增大；随后，摩擦振动能量逐渐平稳，摩擦振动吸引子体积趋于稳定。图3中深黑色区域为摩擦振动吸引子，从图3(a)～图3(b)可以看出从磨合开始到磨合10 min，摩擦振动吸引子体积有增大趋势；然而从图3(b)～(g)看出，磨合10 min至磨合结束，摩擦振动吸引子体积变化差别不大，很难精确识别摩擦副从磨合磨损阶段进入稳定磨损阶段的时刻。

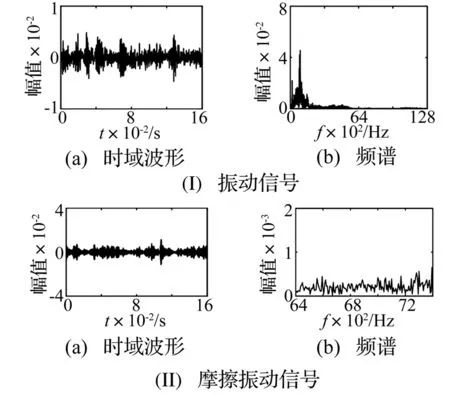
图2 信号时域波形和频谱Fig.2 Waveforms diagrams and spectrums of signals

3.2 摩擦振动吸引子特征参数的变化规律

为了精确识别摩擦副磨合磨损过程中摩擦振动吸引子的体积变化，对摩擦振动吸引子相空间通过式(5)构建奇异值特征向量并由式(6)和式(7)提取摩擦振动吸引子特征参数K。图4为磨合磨损过程中摩擦振动吸引子特征参数的变化曲线。从图4中可以看出，磨合开始，吸引子特征参数K较小，为9.36；随磨合进行，吸引子特征参数K逐渐增大；43 min后，K值达到24.72，并在其附近平稳地波动。由上述分析可见，摩擦振动吸引子特征参数K能够定量地反映磨合过程中摩擦振动吸引子的体积变化，即摩擦振动能量的变化。摩擦副磨合磨损状态的变化可通过摩擦因数进行表征。图5为摩擦副磨合磨损过程中摩擦因数随磨合时间的变化曲线。从图5可以看出，摩擦因数与图4中的摩擦振动吸引子特征参数K同样具有从小逐渐增大并于43 min后处于平稳波动状态。因此，摩擦振动吸引子特征参数K与摩擦因数对磨损阶段的判断一致，可用于摩擦副的磨损状态识别。

图3 摩擦振动吸引子随磨合时间的变化Fig.3 Temporal variation of friction vibration chaotic attractors

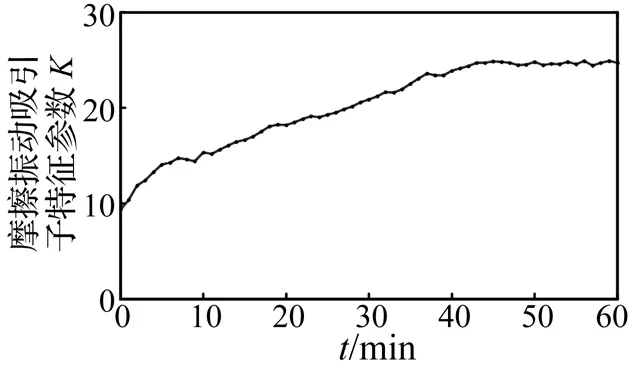
图4 摩擦振动吸引子特征参数K随磨合时间的变化曲线Fig.4 Temporal variation of the energy feature parameter K of friction vibration

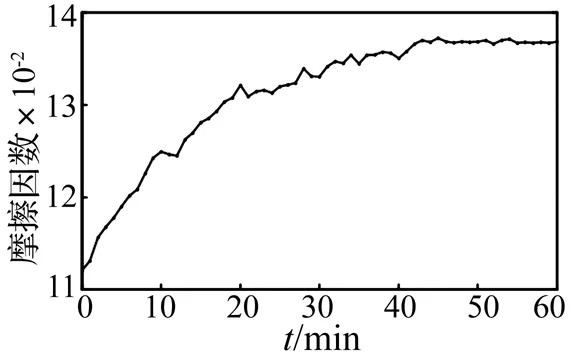
图5 摩擦因数随磨合时间的变化曲线Fig.5 Temporal variation of the friction coefficient μ

4 结 论

本文通过提取摩擦振动吸引子特征参数K并研究其在摩擦副磨合磨损过程中的变化规律研究摩擦振动能量的变化，得出如下结论：

(1)通过摩擦振动吸引子相空间矩阵进行奇异值分解，利用奇异值构建奇异值特征向量并提取其特征参数实现了摩擦振动吸引子特征参数K的提取；

(2)摩擦振动吸引子特征参数K能定量反映摩擦振动吸引子的体积大小，即摩擦振动能量的高低；

(3)摩擦振动吸引子特征参数K与摩擦因数对磨损阶段的判断一致，摩擦振动吸引子特征参数K可用于摩擦副的磨损状态识别。

[ 1 ] 朱华,葛世荣.摩擦学系统的混沌特性[J].机械工程学报, 2004,40(12):10-13. ZHU Hua, GE Shirong. Chaotic characteristics of tribological systems [J]. Chinese Journal of Mechanical Engineering, 2004, 40(12):10-13.

[ 2 ] 姬翠翠. 基于混沌与分形理论的缸套-活塞环磨损过程动力学行为研究 [D].徐州：中国矿业大学，2012.

[ 3 ] 朱华，葛世荣．摩擦力和摩擦振动的分形行为研究 [J]．摩擦学学报，2004，24(5): 433-437. ZHU Hua, GE Shirong. Study on the fractal behaviors of frictional forces and vibration [J]．Tribology，2004，24(5): 433-437.

[ 4 ] LI Guobin, HUANG Yehua, LIN Yuanhua, et al. Multifractal analysis of frictional vibration in the running-in process [J]. Tribology Transactions, 2013, 56(2):284-289.

[ 5 ] 葛世荣，朱华． 摩擦学复杂系统及其问题的量化研究方法 [J]． 摩擦学学报，2002，22(5): 405-408. GE Shirong, ZHU Hua．Complicate tribological systems and quantitative study methods of their problems [J]. Tribology，2002，22(5): 405-408.

[ 6 ] 温诗铸，黄平. 摩擦学原理 [M]. 北京: 清华大学出版社, 2008.

[ 7 ] SUN Di, LI Guobin, WEI Haijun, et al. Experimental study on the chaotic attractor evolvement of the friction vibration in a running-in process [J]. Tribology International, 2015, 88:290-297.

[ 8 ] 孙迪，李国宾，魏海军，等. 磨合过程摩擦振动混沌吸引子演变规律 [J]．振动与冲击，2015，34(6): 116-121. SUN Di, LI Guobin, WEI Haijun, et al. Evolvement rule of frictional vibration chaos attractors in running-in process [J]．Journal of Vibration and Shock，2015，34(6): 116-121.

[ 9 ] LIU Ting, LI Guobin, WEI Haijun, et al.Experimental observation of cross correlation between tangential friction vibration and normal friction vibration in a running-in process [J]. Tribology International, 2016, 97:77-88.

[10] TAKENS F. Detecting strange attractors in turbulence dynamical systems and turbulence[J]. Lecture Notes in Mathematics,1981, 898:366-381.

[11] 杨勇，李立浧，杜林，等．采用时频矩阵奇异值分解和多级支持向量机的雷电及操作过电压识别[J]．电网技术，2012，36(8)：31-37． YANG Yong，LI Licheng，DU Lin，et al．Lightning and switching overvoltage identification based on singular value decomposition of time-frequency matrix and multi-level support vector machine[J]．Power System Technology，2012，36(8)：31-37．

[12] 程军圣，于德介，杨宇．基于EMD 和奇异值分解技术的齿轮故障诊断方法[J]．振动工程学报，2004，17(增刊1)：461-463． CHENG Junsheng，YU Dejie，YANG Yu．A fault diagnosis approach for roller bearings based on EMD method and singular value decomposition technique[J]．Journal of Vibration Engineering，2004，17(Sup1)：461-463．

[13] SUN Di, LI Guobin, WEI Haijun et al. Investigation on friction vibration behavior of tribological pairs under different wear states [J]. Journal of Tribology-Transactions of the ASME, 2015, 137(2):021606.

Feature parameter extraction of a friction vibration attractor based on singular value decomposition

LIU Ting1, LI Guobin1, WEI Haijun2, MU Xue3, XING Pengfei1

(1. Marine Engineering College, Dalian Maritime University, Dalian 116026, China; 2. Merchant Marine College, Shanghai Maritime University, Shanghai 200135, China; 3. Cosco(Dalian) International Freight CO., Ltd., Dalian 116001, China)

An attractor feature parameterKwas defined to quantitatively study a friction vibration attractor, and its variation was investigated in the running-in wear process.Kwas the feature parameter of the eigenvectors built with the attractor phase-space-matrix singular values obtained using the C-C method and the phase-space reconstruction theory. Results showed that friction vibration energy is lower in the beginning stage, the attractor volume is smaller andKis 9.36; when the running-in continues, the friction vibration energy increases, the attractor volume gets larger andKalso increases gradually; friction vibration energy is stable after 43 min, attractor volumes are also stable andKfluctuates near 24.72; therefore,Kcan be used to quantitatively analyze the variation of friction vibration energy in the running-in process; the identification of wear state withKis consistent with that using friction coefficient, andKcan be used to monitor the wear state of tribological pairs.

friction vibration; singular value decomposition; attractor; feature parameter

国家高技术研究发展计划项目(863) (2013AA040203)

2016-05-23 修改稿收到日期：2016-06-15

柳霆 男，博士生，1989年12月生

李国宾 男，博士，教授，1970年3月生

TH212；TH213.3

A

10.13465/j.cnki.jvs.2017.03.027