基于互易原理和空间平均的水下传递函数测量

程 果， 陈景兵， 何 琳

(1. 海军工程大学 船舶振动噪声国家重点实验室，武汉 430033； 2. 海军工程大学 振动与噪声研究所，武汉 430033)

基于互易原理和空间平均的水下传递函数测量

程 果， 陈景兵， 何 琳

(1. 海军工程大学 船舶振动噪声国家重点实验室，武汉 430033； 2. 海军工程大学 振动与噪声研究所，武汉 430033)

提出了不均匀混响声场中扩散声场互易传递函数的测量方法。通过交换激励位置和测量位置，互易测试可以回避正向测试中所遇到的激励空间狭小，受激结构脆弱等问题。基于空间平均方法，可以在混响声场中得到扩散声场传递函数。结合互易传递函数测量技术和虚拟力重构技术，可以仅依靠振动数据评估水下结构辐射噪声。通过数值仿真和湖上试验验证了上述理论。仿真和试验结果表明，提出的方法可以应用于复杂水下结构，有效消除不均匀混响声场的影响。相关工作可以为互易原理和空间平均方法的研究提供参考。

传递函数；互易原理；空间平均；混响声场；水下测试

传递函数是建立结构物振动与辐射噪声之间关联的重要系统特性，工程中的获得方法通常是开展大量激振测试。在实际操作的过程中，许多水下结构的测试往往是在不均匀的混响声场环境中进行[1]。混响声场不同于严格的扩散声场，其声能分布不均匀，声压波动较大，利用这类环境中采集的数据难以直接获得有意义的结论[2]。

空间平均的方法为解决这类问题提供了很大便利[3-5]。通过在多个测量位置进行测量，并将测量数据平均，消除源场不均匀性所造成的影响。但是，对于复杂结构，尤其是水下复杂结构的传递函数测试，空间平均的方法的应用难度较大。主要是因为空间平均的方法需要进行大量测试，而复杂结构往往内部空间狭小、部分结构脆弱，大型激振设备难以布置且无法施加足够强度的激励，传统激振测试难以实施。

针对上述工程应用难题，提出了一种将空间平均测量法与互易测量法相结合的方法：运用互易原理开展传递函数的测量，通过外部声源激励结构物，回避传统激振测试的困难[6]；基于空间平均的方法，在正向实测结果与互易评估结果之间建立了稳定的联系。本文首先介绍了相关的理论基础，然后对提出方法的正确性进行了仿真和试验验证，最后对试验结果进行了讨论总结。

1 基础理论

1.1 平均声压

为了在不均匀混响声场中建立稳定的互易关系，不妨首先讨论混响声场中平均声压的评估问题。

假设在一个功率固定且无指向性的水下声源附近放置有一个水听器，与水下声源的相对距离为r，在稍远一些的位置也放置有一个水听器，与水下声源的相对距离为R。当水下声源开始激励时，两个水听器都可以测量到相应位置的声压响应：u1(r)和w1(R)。

将水下声源和两个水听器移动到新的测量位置，同时保持三者之间的相对位置不变，再次开启水下声源，两个水听器则测量到当前位置的声压响应u2,w2。尽管水下声源的功率没有变化，但是由于声场的不均匀性，当前位置的声压响应值与原位置的声压响应值很可能是不同的。

重复上述测量步骤，选择多个测量位置进行测量，就可以得到多个位置的响应声压：

u1,u2,…uN;w1,w2,…wN

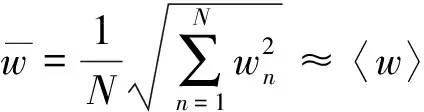
(1)

(2)

1.2 声源强度

对于功率已知的水下声源，声源体积速度是可以直接计算得到的。对于功率未知的水下声源，声源体积速度则依靠以下公式计算：[8]

(3)

式中:U(f)为声源在频率为f时的体积速度，j为虚数符号，k为波数，d为水下声源发声半径，u′(r,f)为距离声源中心r′处，频率为f时的自由声场响应声压，ρ0为介质密度。当水下声源体积较小且只考虑低频时，式(3)也可以简化为：

(4)

但是，上述公式中的声压值是自由场环境中的测量值。混响场的平均声压值与自由场的声压值之间，存在比例关系，比值与声场吸声系数s(f)有关。获取混响声场的吸声系数有很多方法，不是本文的讨论重点，就不再详述了。

利用水下声源附近的水听器测量数据，就可以得到水下声源体积速度的评估值。

(5)

结合式(2)，水下声源体积速度平均值与响应声压平均值之间的比值可以表示为：

(6)

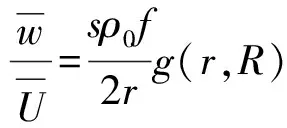
1.3 互易关系

假设使用了两个不同的水下声源在同一混响环境中进行了测试，每次测量位置都是随机选取，测量次数都足够多，那么就可以得到两组平均响应声压和平均体积速度：

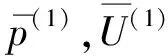
如果两组测试中，水下声源与水听器的相对位置是相同的，那么：

(7)

这样就证明了在混响场中的声学平均互易关系。

(8)

结合式(6)，式(8)也可以表示为：

通过利用水下声源激励结构，测量速度响应，得到平均传递函数。将平均传递函数与平均激励力相结合，也能评估该环境下水下结构的平均辐射声压。

(9)

需要指出的是，即使水下声源或水下结构的功率难以保持恒定不变，只要其功率稳定，符合中心极限定律，那么当测量位置和次数足够多时，也有式(9)的关系。

1.4 虚拟力重构

在实际水下结构中，激励力F是难以获取的。设备机脚通常不是一个点，而是一个较大的平面，且不能随意拆卸，使用力传感器直接测量困难较大。虚拟力重构技术为解决这类问题带来了很大方便。

在实际设备上选取若干虚拟力重构点，并在设备周围选取若干响应参考点，测量重构点与参考点之间的导纳矩阵[A]。例如力锤敲击试验就可以测量得到导纳矩阵：

[A]=[a′]/[F′]

(10)

式中:[F′]是力锤在各个重构点的激励力矩阵，[a′]是参考点的响应加速度矩阵。虽然导纳矩阵与结构的浸水状态有关，但在浸水深度变化不大的情况下，可以近似看作是恒定值。当设备开启时，只需要测量参考点的加速度{a}，就可以实时获取重构点的激励力{F}。

{F}=[A]+{a}

(11)

式中:[A]+为导纳矩阵的广义逆。在很多时候，求解[A]+需要进行正则化以避免矩阵求逆时的病态问题。[12]

在实际应用中，在声场不同进行多次测量，得到的参考点加速度不尽相同，因此，每次重构的虚拟力也不一样。

(12)

(13)

对虚拟力求平均实质上是对参考点的加速度响应求平均。式(9)可以改写为：

(14)

2 数值仿真

2.1 仿真模型

不妨假设测量环境是一个深度不均匀的浅海海域，深度约在7～9 m不等。测试对象为一个双层圆柱壳体模型，模型长2 m，外壳直径1.8 m，厚2 mm，内壳直径1.4 m，厚8 mm，两端为25 mm厚盖板。其内部有一个激励源，可以提供稳定的激励力，激励力的幅值取于30～35 N。水下声源为无指向性恒定功率声源。为讨论方便，假设海底的吸声系数为0.5，系统满足互易适用性条件。

为减少计算量，建立半双层圆柱壳体模型并在中线处施加对称边界条件，以模拟整个双层圆柱壳体计算结果，如图1所示。基于该模型，仿真以下测试工况。

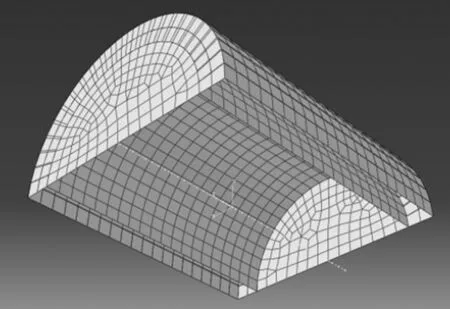
图1 数值仿真模型Fig.1 The model of numerical simulation

(1)关闭水下结构内的激励源，在距离结构5.7 m处，使用水下声源激励结构，测量结构内激励源处的速度响应；

(2)收起水下声源，打开水下结构内的激励源，在水下声源处使用水听器测量外部响应声压；

(3)在不同位置，重复步骤(1)、(2)的测试，并对结果求平均，得到正向和互易测得的传递函数。

2.2 仿真结果

以激励力32 N，水深8 m为例，计算5.7 m处辐射噪声如图2所示。以400 Hz频点为例，辐射噪声134.1 dB，根据式(8)可知，传递函数值为104.0 dB。随机生成20组正向和互易测试结果，可以得到传递函数(总级)不同次数平均效果，如图3所示。

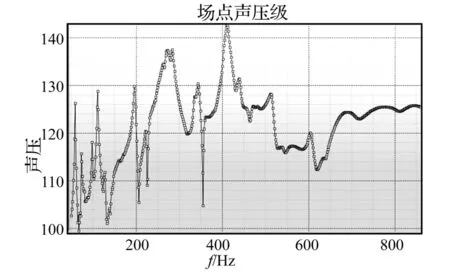
图2 辐射噪声计算值Fig.2 The calculated result of the radiated noise

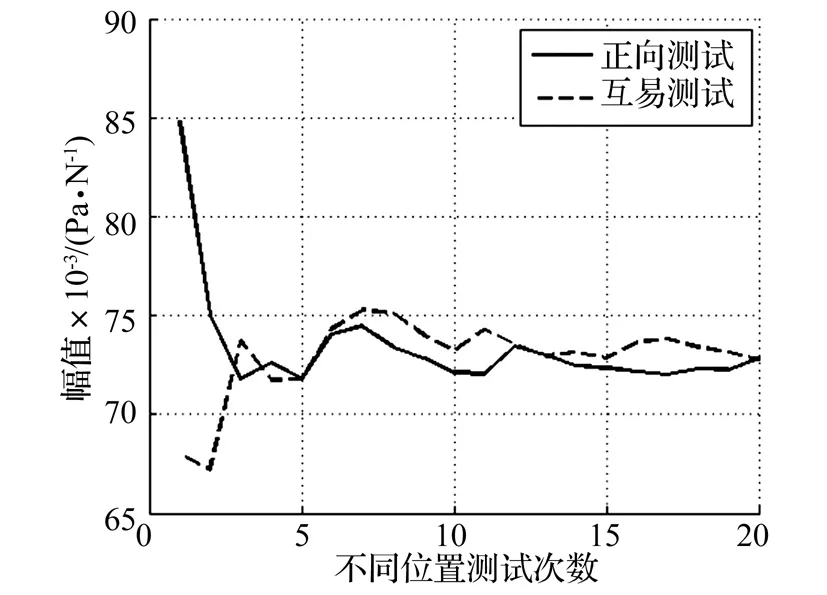
图3 辐射噪声传递函数Fig.3 Transfer functions of radiated noise

从图3可以看到：①经过一定次数的平均处理，互易测试的结果能够较好的反映正向测试的结果；②平均3次以上的结果已经比较稳定，互易和正向测试的误差较小。这是因为在设定仿真条件时，测量环境变化的波动较小。如果在环境变化较大的区域进行上述测试，需要的测试次数就要多一些。

3 试验验证

3.1 试验环境

在千岛湖对上述理论方法进行了试验验证。千岛湖为淡水湖，试验区域选在一个水湾内部，水深7～9 m，距离岸边10～100 m。水湾内部风浪较小，背景噪声也较小，能够满足试验要求。

试验结构为双层圆柱壳体模型，长2.05 m，外壳直径1.78 m，厚2 mm，内壳直径1.46 m，厚8 mm，壳间由四根均匀分布的环形肋骨支撑。壳体两端由25 mm厚的不锈钢板密封，内外层间充水。壳体内部固定有平板，平板厚8 mm。模型内部安装有小型空气压缩机，空气压缩机的进气阀和排气阀同时打开，并在机脚等位置安装有加速度计。模型内部设备依靠穿过壳体端盖的水密电缆供电，内部振动信号则经由水密信号线缆向外传输。

对于一般机械设备，选取6个虚拟力重构点即能较为准确的描述设备的激励状态[13]。实际操作过程中，在空气压缩机机脚附近共选取了7个虚拟力重构点，即重构7组虚拟力。

图4 双层圆柱壳体模型Fig.4 The double-layer cylindrical shell

试验所使用的水下声源为电火花脉冲声源，其激励强度可以通过调整充电电压改变。由于充电电压无法精确控制，有时激励强度略有不同。壳体模型由吊车吊放入水，水下声源和用于测量体积速度的水听器则固定于船上。基于前期研究结果[6]，在混响声场中应选取多支水听器在不同角度同时进行水下声源体积速度的评估。本次试验综合考虑工程实现难度，选取了4支水听器用于测量水下声源的体积速度。

3.2 试验流程

根据上述理论分析，试验按照如下步骤进行：

(1)吊放模型至水下，水下声源用缆绳固定于停泊在水湾内的船舷上，距离模型5.7 m；在水下声源周围四个对称的位置布置水听器，距离水下声源2 m。

(2)利用声源执行脉冲激励，测量声源周围的声压响应和模型内部加速度响应。

(3)收起水下声源，将水听器放置于原水下声源的位置。

(4)开启模型内部空气压缩机，测量模型内振动加速度响应和外部的声压响应，并进行虚拟力重构，求得空气压缩机的等效输出力。

图5 湖上试验环境Fig.5 The environment of the lake experiment

(5)更换试验位置，重新保持声源和模型相对位置不变，重复步骤(1)～(5)的工作。

(6)将步骤(2)、(4)、(5)的试验数据代入式(14)，得到试验区域平均的正向辐射声压和互易评估声压。

3.3 试验结果

首先考察不同位置的互易辐射声压评估结果，如图 6所示，在各个频段的声压评估结果差距较大。

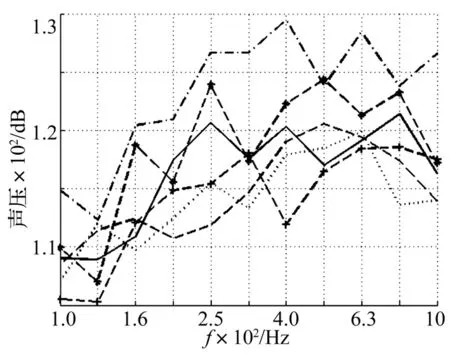
图6 各测量位置辐射噪声互易评估Fig.6 The reciprocal evaluation of radiated noise in different positions

图中实线是经过平均处理后的声压评估值，各虚线是单独利用各点数据的互易评估值。不同位置的最大评估差距接近20 dB，与平均值的最大差距也超过了10 dB。显然，这一差距与声场环境有关，声场分布越不均匀，这一差距就越大。

然后考察多次测试平均后的正向实测辐射声压和互易评估辐射声压,如图7所示。

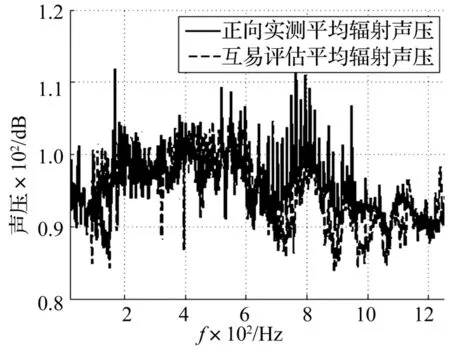
图7 平均辐射噪声对比Fig.7 The comparison of the average radiated noise

在图上可以看出，正向实测值和互易评估值趋势一致，在部分频点的线谱上还有一定的误差。上述误差在三分之一倍频程谱上可以更清晰的反映。

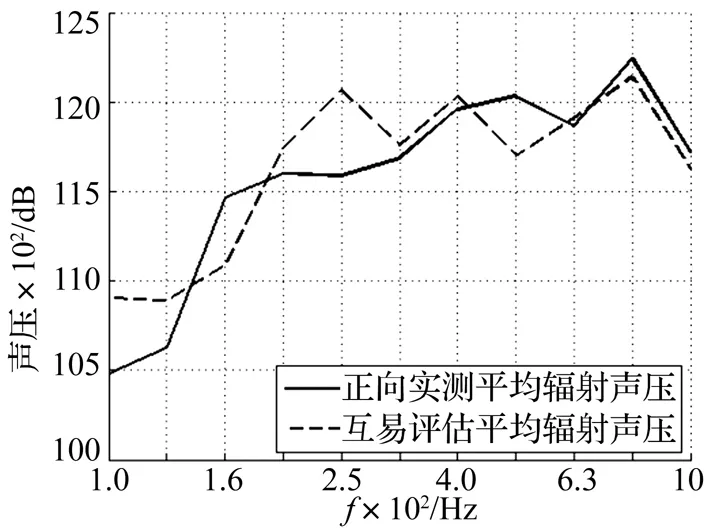
图8 平均辐射噪声对比(三分之一倍频程频带级)Fig.8 The comparison of the average radiated noise(In the third octave spectrum)

如图 8所示，互易评估误差在3～5 dB以内。部分频段误差相对较大，主要是虚拟力重构、声场不确定性和双层壳体模型非线性等因素引起的。

可以发现，尽管声场存在较大的不均匀性，最终的评估结论则相对稳定。事实上，声场的不均匀性越强，这一对比就越明显，提出的方法的优势就越大。

4 结 论

针对水下复杂结构在不均匀混响声场中的振动和辐射噪声关系评估的问题，提出了一套互易测试与空间平均相结合的方法，经数值仿真和湖上试验验证，形成结论如下：

(1)提出的方法能够仅利用不均匀混响声场中的测试数据，求解扩散声场中的辐射噪声传递函数；

(2)利用提出的方法并基于振动数据进行扩散声场中的辐射噪声评估，误差在3～5 dB以内。

相关工作不仅有助于互易原理和混响声场的理论研究，也能为水下辐射噪声评估和预报提供参考。

[ 1 ] 孟春霞，杨士莪，张亮，等. 船舶辐射噪声源模型的试验验证[J]. 振动与冲击，2009，28(11)：6-8. MENG Chunxia, YANG Shie, ZHANG Liang, et al. Validity test of radiated noise sources model of ship[J]. Journal of Vibration and Shock, 2009, 28(11):6-8.

[ 2 ] 郭荣，裘剡，房怀庆，等. 频域传递路径分析方法(TPA)的研究进展[J]. 振动与冲击，2013，32(13)：49-55. GUO Rong, QIU Shan, FANG Huaiqing, et al. Advance in studying on transfer path analysismethods in frequency domain[J]. Journal of Vibration and Shock, 2013, 32(13):49-55.

[ 3 ] DUCOURNEAU J, PLANEAU V, CHATILLON J, et al. Measurement of sound absorption coefficients of flat surfaces in a workshop[J]. Appl Acoust, 2009, 70:710-721.

[ 4 ] 尚大晶，李琪，商德江，等. 水下声源辐射声功率测量实验研究[J]. 哈尔滨工程大学学报，2010，31(7)：938-944. SHANG Dajing, LI Qi, SHANG Dejiang, et al. Measurement of the radiated power of sound sources in a reverberation pool[J]. Journal of Harbin Engineering University, 2010, 31(7):938-944.

[ 5 ] DUCOURNEAU J, FAIZ A, KHANFIR A, et al. Measuring sound scattering coefficients of uneven surfaces in a reverberant workplace Principle and validation of the method[J]. Appl Acoust, 2013, 74:653-660.

[ 6 ] 程果，徐荣武，何琳，等. 混响声场条件下水声互易传递函数的测量及应用[J]. 声学学报，2014，39(5)：577-581. CHENG Guo, XU Rongwu, HE Lin, et al. Application and measurement of underwater acoustic reciprocity transfer functions in reverberant sound field[J]. Acta Acustica, 2014, 39(5):577-581.

[ 7 ] LUBMAN D, WATERHOUSE R V, CHIEN C S. Effectiveness of continuous spatial averaging in a diffuse sound field[J]. J. Acoust. Soc. Am., 1973, 53(2):650-659.

[ 8 ] WOLDE T T, VERHEIJ J W, STEENHOEK H F. Reciprocity method for the measurement of mechano-acoustical transfer functions[J]. J. Sound Vib., 1975, 42(1):49-55.

[ 9 ] FAHY F J. The Vibro-acoustic reciprocity principle and applications to noise control[J]. ACUSTICA, 1995, 81:544-558.

[10] CHENG Guo, XU Rongwu, HE Lin. Application and measurement of underwater acoustic reciprocity transfer functions with impulse sound sources[C]//Vibroengineering PROCEDIA, 2015, 5:48-52.

[11] WOLDE T T. Reciprocity measurements in acoustical and mechano-acoustical systems-review of theory and applications[J]. Acta Acustica United with Acustica, 2010, 96: 1-13.

[12] 卢丁丁，何琳，程果，等. 评估设备激励特性的虚拟力方法研究[J]. 船舶力学，2013，17(10)：1169-1175. LU Dingding, HE Lin, CHENG Guo. Research on pseudo-forces method used in characterization of machine force[J]. Journal of ship mechanics, 2013, 17(10):1169-1175.

[13] JANSSENS M H A, VERHEIJ J W. A pseudo-forces methodology to be used in characterization of structure-borne sound sources [J]. Applied Acoustics, 2000, 61: 285-308.

Measurement of underwater transfer functions using spatial average and reciprocity principle

CHENG Guo, CHEN Jingbing, HE Lin

(1.National Key Laboratory on Ship Vibration & Noise, Naval University of Engineering, Wuhan 430033, China;2. Institute of Noise and Vibration, Naval University of Engineering, Wuhan 430033, China)

The measurement method of reciprocity transfer functions of diffuse sound fields in anomalous reverberant sound fields was proposed. Through reversing actuating points and measuring points in reciprocity measurement, the problems of direct-actuating measurements, such as narrow spaces and friable structures were avoided. Based on the spatial average method, the underwater radiated noise transfer functions of diffuse sound fields were obtained in reverberant sound fields. These transfer functions and the pseudo-force method were used to evaluate the radiated noise of underwater structures. This theory was validated with numerical simulations and a lake test. The results of simulations and tests showed that the proposed method can be applied in complex underwater structures to eliminate the influences of anomalous reverberant sound fields. The resalts provided a reference for further studying the reciprocity principle and the spatial average method.

transfer function; reciprocity principle; spatial average; reverberant field; underwater measurement

国家自然科学基金(51209214)

2016-01-27 修改稿收到日期：2016-05-30

程果 男，博士生，1988年12月生

何琳 男，教授，博士生导师，1957年11月生

TB532；TB52.1

A

10.13465/j.cnki.jvs.2017.03.024